�E��b���w
�y�ڎ��z
(1) ���w�����̕���
���������w�I�ɕ��ނ���ƁA�u������(pure substance)�v�Ɓu������(mixture)�v�ɕ����邱�Ƃ��ł��܂��B�������͈��̐����������A���fN2�␅H2O�̂悤�ɁA1�̉��w���ŏ������Ƃ��ł��镨���ł��B���������\�����Ă��邻�ꂼ��̌��f�̑g���▧�x�A�Z�_�A���_�Ȃǂ͈��ł���A�����̕����I��������A�������̎�ނʂ��邱�Ƃ��ł��܂��B����ɑ��āA�������͕����̏��������������Ă��镨���ł��B�������́A�������Ă��镨���̎�ނƂ��̍�����ɂ���āA�������قȂ�܂��B��C�͐g�߂ɂ��鍬�����ł���A��C�͒��fN2��_�fO2�A�A���S��Ar�A��_���Y�fCO2�Ȃǂ̍������ł��B���R�E�̕����͍������ł��邱�Ƃ������A�C�����A�Ζ��Ȃǂ͍������ł��B�܂��A�������͂���Ɂu�P��(simple substance)�v�Ɓu������(compound)�v�ɕ����邱�Ƃ��ł��܂��B�P�̂͒��fN2�̂悤�ɒP��̌��f����\������鏃�����ł���A�������͐�H2O�̂悤�ɕ����̌��f����\������鏃�����ł��B
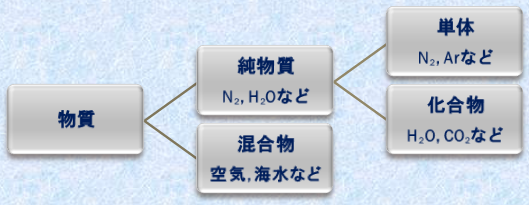
�}.1 �����̕���
�܂��A�����̐���������ł����Ă��A���w�\���̈Ⴂ�ɂ��A�قȂ鐫�����������������݂��邱�Ƃ�����܂��B�����̕����̊W���u���f��(allotrope)�v�Ƃ����܂��B���f�̂́A�����P��̌��f����Ȃ�P�̂ł����A���w�I�����╨���I���������Ȃ�Ⴂ�܂��B��\�I�ȗ�Ƃ��ẮA�u�_�C�������h(diamond)�v�Ɓu����(graphite)�v���A�݂��ɒY�fC�̓��f�̂ł��B�����́A�ǂ�������w���ŏ����ΒY�f��C�ł����A���q�̔z��⌋���l�����قȂ邽�߂ɁA���ꂼ�ꂪ�S�������������������̂ł��B�_�C�������h�͖��F�����ōd���A�d�C�`����������܂��A�����͍��F�œ�炩���A�d�C�`����������܂��B�Y�fC�̑��ɂ́A����S��_�fO�A����P�Ȃǂɓ��f�̂����݂��܂��B
�\.1 ��ȓ��f��
|
���f |
���f�� |
���w�� |
�����Ȃ� |
|
����S |
������ |
S8 |
���F����B�퉷�ōł�����B |
|
�P���� |
S8 |
���F�j���B95.3���ȏ�ł͈���B |
|
|
�S���� |
Sx |
���F����`�Œe��������B���x��������ƈÊ��F�ɂȂ�B |
|
|
�Y�fC |
�_�C�������h |
C(���啪�q) |
���F���������B�M�`�����������A�z�����ōł��d���B |
|
����(�O���t�@�C�g) |
C(���啪�q) |
���F�ő́B�w��ɔ�����₷���B�d�C�`����������B |
|
|
�t���[���� |
C60�AC70�Ȃ� |
���q�B���w�������ɕx�ށB |
|
|
�J�[�{���i�m�`���[�u |
Cx |
�~���q�B���x�ɗD��A�F���G���x�[�^�̍ޗ��B |
|
|
�O���t�B�� |
Cx |
�����̈�w�ɑΉ����錴�q�w�B�M�`�����͂��ׂĂ̕������ōő�B |
|
|
�_�fO |
�_�f |
O2 |
���F���L�̋C�́B��C���ɖ�21%���݂���B |
|
�I�]�� |
O3 |
�W�F�œ��ُL�̋C�́B���w���ŃI�]���w���`���B |
|
|
����P |
������ |
P4 |
�L�ł̒W���F�ő́B��C���Ŏ��R������̂Ő����ŕۑ��B |
|
�ԃ��� |
Px |
�Ԋ��F�ő́B�}�b�`���̑���ɗ��p����Ă���B |
(2) ���q�̍\��
�������\������ł���{�I�ȗv�f���A�u���f(element)�v�Ƃ����܂��B���f�́A�������q�ԍ��́u���q(atom)�v�ɂ���đ�\����镨���̎�ʖ��̂��Ƃł��B���f�Ƃ����T�O�́A�Ñ�M���V�A�̎��R�N�w�҂������l���o�������̂ł��B�����́A���E��C�E�Ȃǂ����f�Ƃ����u�ꌳ�_(monism)�v�ƁA��C�E���E�y�E��4���f�����肷��u�����_(pluralism)�v�̗��ꂪ����܂����B���{�ł́A���w�҂Ŗ��{�V�����؏��a����p�̉F�c����佂��A�E�B���A���E�w�����[�̒����uElements of Experimental Chemistry(1799�N)�v�̃I�����_���̘a�u�ɖ��J�@(1837�N)�v�ŁA���߂āu���f�v�Ƃ������t���g�����Ƃ����Ă��܂��B�u�ɖ�(������)�v�́A�I�����_��ʼn��w�̈ӂ́uChemie(�V�F�~�[)�v�̉���ł��B�ɖ��J�@�́A�]�ˎ���ɏo�ł��ꂽ���w���Ƃ��Ă͍ł���������Ă���A�����̏����܂œǂ܂ꑱ���܂����B
���݁A���f��118��ނ��m���Ă���A�e���f�ɌŗL�̌��q�����݂��܂��B���f�̂����A��90��ނ͎��R�E�ɑ��݂��A���̌��f�́A����������ȂǂŐl�H�I�ɍ��ꂽ���̂����B����A���f�͂���ɍ�������Ă����ƍl�����Ă���A�t�B�������h�̕����w�҂ł���y�b�J�E�s���[�R�b�N�ɂ��A172�Ԍ��f�܂ł������\�炵���ł��B�������A�����ɂ���Ė{���Ɍ��f������Ă݂Ȃ���A�{���̂Ƃ���͕�����܂���B���q�ԍ����傫���Ȃ�قǁA���f����������͓̂���Ȃ邱�Ƃ��\�z����Ă���̂ŁA�������������Ă��邤���Ɏ����\���������邱�Ƃ͂Ȃ��ł��傤�B�e���f�́A���e���ꖼ�Ȃǂ̓����������������f�L��(�啶��)�ŕ\����܂��B�������A�������������ɂȂ�ꍇ�ɂ́A����1����(������)��Y���ċ�ʂ��܂��B
�\.2 ���f�ƌ��f�L���̗�
|
���f�� |
���f�L�� |
���e���ꖼ |
�p�ꖼ |
���f���̗R�� |
|
���f |
H |
Hydrogenium |
Hydrogen |
��������� |
|
�w���E�� |
He |
Helium |
Helium |
���z |
|
�Y�f |
C |
Carboneum |
Carbon |
�ؒY |
|
���f |
N |
Nitrogenium |
Nitrogen |
�ɐ��琶������� |
|
�_�f |
O |
Oxygenium |
Oxygen |
�_������� |
|
�i�g���E�� |
Na |
Natrium |
Sodium |
�ő� |
|
���� |
S |
Sulfur |
Sulfur |
�̂��� |
|
���f |
Cl |
Chlorum |
Chlorine |
���ΐF |
|
�J���E�� |
K |
Kalium |
Potassium |
���؊D |
|
�S |
Fe |
Ferrum |
Iron |
�ł��A���� |
|
�� |
Cu |
Cuprum |
Copper |
���z�R�̂���L�v���X�� |
|
�� |
Ag |
Argentum |
Silver |
�P���A���邢 |
|
�� |
Au |
Aurum |
Gold |
�����A�ł̏��_ |
���q�́A�������\�������{�I�ȗ��q�ł��B�u���q�v�Ƃ����T�O���ŏ��ɒ����̂́A�Ñ�M���V�A�̓N�w�҃f���N���g�X�ł���Ƃ����Ă��܂��B�f���N���g�X�́A�u���������Ă����ƁA�ŏI�I�ɂ���ȏ�͕����ł��Ȃ����q�ɂȂ�͂����v�ƍl���A���̍ŏ����̒P�ʂ��u���q�v�ƌĂ̂ł��B�u���q(atom)�v�́A�M���V�A��́uatomos(�����ł��Ȃ�)�v�ɗR�����錾�t�ł��B���q�́A���S�ɂ��鐳�d�ׂ�тт��u���q�j(atomic nucleus)�v�ƁA���̎���ɂ��镉�d�ׂ�тт������́u�d�q(electron)�v���琬�藧���Ă��܂��B���q�j�́A���d�ׂ����u�z�q(proton)�v�Ɠd�ׂ������Ȃ��u�����q(neutron)�v����\������܂��B�܂�A�f���N���g�X�́A���q���u����ȏ�͕����ł��Ȃ��ŏ��P�ʁv�ƍl������ł����A���ۂɂ́A����ɗz�q�⒆���q�A�d�q�Ƃ��������q�ɕ������邱�Ƃ��ł����ł��B
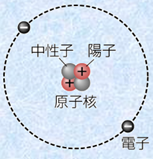
�}.2 ���q���f��
�z�q�Ɠd�q�́A�݂��ɕ��������œ����傫���̓d�ׂ������Ă���A�z�q���{e�A�d�q��-e�̓d�ׂ������܂��B�z�q�Ɠd�q�̓d�C�ʂ��}1.602�~10-19 C�ŁA����͓d�C�ʂ̍ŏ��P�ʂł���A�u�d�C�f��(elementary electric charge)�v�Ƃ����܂��B�d�C�I�ɒ����Ȍ��q�ł́A�z�q�Ɠd�q�݂͌��ɐ����̓d�ׂ�ł����������̂ŁA���q�j���̗z�q�̐��Ɠd�q�̐��͓������Ȃ�܂��B
�\.3 �z�q�y�ђ����q��d�q�̎��ʂƓd��
|
���q |
�d�C�� |
�d�� |
���� |
���ʔ� |
|
|
���q�j |
�z�q |
�{1.602�~10�|19 C |
�{1 |
1.673�~10�|24 g |
1,840 |
|
�����q |
0 C |
0 |
1.675�~10�|24 g |
1,840 |
|
|
�d�q |
-1.602�~10�|19 C |
-1 |
9.109�~10�|28 g |
1 |
|
���q�j���̗z�q�̐��́A���f�̎��ނɂ���Ă��ׂĈقȂ�A�z�q�̐������̌��q�́u���q�ԍ�(atomic number)�v�Ƃ����܂��B�Ⴆ�A���fH�͗z�q��1���̂Ō��q�ԍ���1�ƂȂ�A�_�fO���z�q��8���̂Ō��q�ԍ���8�ƂȂ�܂��B�܂��A���q�j���̒����q�̐��́A���q�̎�ނɂ���ăo���o���ł���A�قƂ�ǂ̌��q���A���q�j���ɉ��������q�������Ă��܂��B�Ȃ��A���f�̎�ނ������Ȃ�A�z�q�̐��͂ǂ̌��q���������Ȃ�܂����A�����q�̐��͓������f�ł��قȂ邱�Ƃ�����܂��B
�z�q�ƒ����q�̎��ʂ͂قړ������A���q�j���̗z�q�ƒ����q�̐��̘a���A���̌��q�́u���ʐ�(mass number)�v�Ƃ����܂��B��������ʐ��ƌĂԂ̂́A�z�q�ƒ����q�̎��ʂ̘a���A���̌��q�̎��ʂƂقƂ�Ǔ���������ł��B�d�C�I�ɒ����Ȍ��q�ł́A���q�j�̎����z�q�̐��Ɠ������̓d�q����芪���Ă��܂����A�d�q�̎��ʂ͗z�q�⒆���q1�̎��ʂ̖�1/1,840�Ɣ��ɏ������̂ŁA�d�q�̎��ʂ͖������Ă��قƂ�ǖ��Ȃ��A���q�̎��ʂ͎����㎿�ʐ��ɂقڔ�Ⴗ�邱�ƂɂȂ�܂��B
�\.4 ���q�ԍ��Ǝ��ʐ�
|
���q�ԍ� |
���q |
���ݔ� |
�z�q�� |
�����q�� |
���ʐ� |
|
1 |
���f1 |
99.9885% |
1 |
0 |
1 |
|
���f2 |
0.0115% |
1 |
1 |
2 |
|
|
6 |
�Y�f12 |
98.93% |
6 |
6 |
12 |
|
�Y�f13 |
1.07% |
6 |
7 |
13 |
|
|
8 |
�_�f16 |
99.757% |
8 |
8 |
16 |
|
�_�f17 |
0.0038% |
8 |
9 |
17 |
|
|
�_�f18 |
0.205% |
8 |
10 |
18 |
���q�����q�ԍ��Ǝ��ʐ����܂߂ĕ\������Ƃ��́A���̐}.3�̂����ɁA���f�L���̍����Ɍ��q�ԍ����A����Ɏ��ʐ���\�L���܂��B�Ȃ��A���ʐ��͌��q�̐��m�Ȏ��ʂ�\���Ă���킯�ł͂Ȃ��Ƃ������Ƃ�O���ɓ���Ă����Ȃ���Ȃ�܂���B�܂��A���f�L���ƑΉ����錴�q�ԍ��͌��܂��Ă��邽�߁A�����̌��q�ԍ��͏ȗ����邱�Ƃ������ł��B
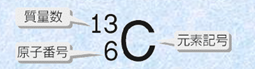
�}.3 ���q�ԍ��Ǝ��ʐ��̕\�L�̎d��
���q�̑傫���́A��ނɂ���Ă����炩�قȂ�܂����A�ǂ̌��q�����a�����0.1 nm (10�|10 m)���x�̑傫���ł��B�Ⴆ�A���q�ԍ�1�̐��f���q�̒��a��0.106 nm�ŁA���q�ԍ�18�̃A���S�����q�̒��a��0.142 nm�ł��B���q�ԍ�95�̃A�����V�E�����q�ł��A���q�̒��a��0.350 nm���x�ɂ����Ȃ�܂���B�A�����V�E�����q�̓d�q�������f���q�̓d�q����95�{�ɂȂ��Ă��A���a�͐��f���q��3.3�{���x�ɂ����Ȃ�Ȃ��̂ł��B���̂悤�ɁA�d�q���������Ă����q�̑傫�������܂�ς��Ȃ����R�́A�d�q����������̂Ɠ����ɁA�t�̓d�ׂ����z�q�̐��������邩��ł��B�d�q����������ƁA�d�q���m�ɃN�[�����͂ɂ��˗͂������āA�d�q�̐�߂�̈悪�L���Ȃ�A���q�͑傫���Ȃ�܂��B�������A�����ɗz�q�������āA���q�j�Ɠd�q�̈��͂������Ȃ�̂ŁA�����ɂ͗��҂̃o�����X�̌��ʁA�d�q�������Ă��A���q�̑傫���͂��܂�ς��Ȃ����ƂɂȂ�̂ł��B
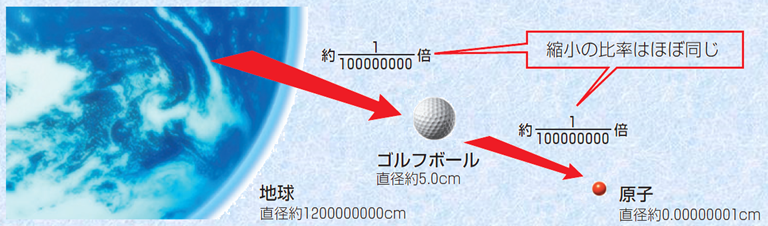
�}.4 ���q�̑傫���̔�r
����ɁA���q�j�̑傫���͂Ƃ����ƁA���f���q�̌��q�j�̒��a��2.40 fm(2.40�~10�|15 m)�ł��B���f���q�̌��q�j�́A���f���q�S�̂̑傫���̖�1/44,000���x�̑傫����������܂���B����́A���q�S�̂̑傫�����h�[������ɗႦ��ƁA���q�j�̑傫���͂ق�1�~�d�݂ɑ������܂��B���q�j���A���q�Ɣ�ׂĂ����ɏ��������������ł���Ǝv���܂��B���Ȃ݂ɁA���q�j�̑傫���̃I�[�_�[�ł���1 fm���A�u1 yukawa�v�ƌĂԂ��Ƃ�����܂��B����́A1949�N�Ƀp�C���Ԏq�̌����Ńm�[�x�������w�܂���܂������{�̕����w�҂ł��铒��G���̖��ɂ��Ȃ�ł��܂�(�C�I�����G�l���M�[�Ɠd�q�e�a�����Q��)�B
�\.5 �����̃I�[�_�[
|
�P�� |
���Z |
���� |
�I�[�_�[ |
|
km |
1 km��1�~103 m |
1,637 m |
�o�C�J����(���E��[����)�̍ő吅�[ |
|
hm |
1 hm��1�~102 m |
100 m |
�T�b�J�[�̃t�B�[���h�̒��� |
|
m |
�| |
1.0 m |
�����w���p���є�6�i�̍��� |
|
cm |
1 cm��1�~10�|2 m |
1.5 cm |
���ϓI�ȉ�̑̒� |
|
mm |
1 mm��1�~10�|3 m |
1.0 mm |
���ϓI�ȃP�W���~�̑̒� |
|
µm |
1 µm��1�~10�|6 m |
1 µm |
�p���h���E�C���X(�ő�̃E�C���X)�̑傫�� |
|
nm |
1 nm��1�~10�|9 m |
2 nm |
DNA�����̒��a |
|
pm |
1 pm��1�~10�|12 m |
1 nm |
�����̔g�� |
|
fm |
1 pm��1�~10�|15 m |
2.4 fm |
���f���q�̌��q�j�̒��a |
(i) ���ʑ̂ƕ��ː����ʑ�
���q�̒��ɂ́A�z�q���͓����ł��A�����q���̈Ⴂ�ŁA���ʐ����قȂ錴�q�����݂���ꍇ������܂��B�����̌��q���A�݂��Ɂu���ʑ�(isotope)�v�Ƃ����܂��B���ʑ̓��m�́A��Ɏ����\�̓����ʒu�ɂ��邽�߁A�M���V�A��́uiso(����)�v�Ɓutopos(�ꏊ)�v���������Č��ꂪ�ł��܂����B���ʑ̗̂�Ƃ��ẮA�V�R�ɑ��݂��鐅�f���q�ɂ́A���ʐ���1��1H (99.9885%)�Ǝ��ʐ���2��2H(0.0115%)������܂��B�܂��A���ʐ���3��3H���A���R�E�ɂ������ʂ������݂��Ă��܂��B���̂悤�ɑ����̌��f�́A�������̓��ʑ̂��A�قڈ��̊����ō����������̂Ƃ��đ��݂��Ă���̂ł��B
���ʑ̂́A���ʐ����قȂ邾���œ������f�ł���A���w�I�����͂قړ������ł��B���ʑ̂́A�����q�̐����قȂ��Ă����q�ԍ��͈ꏏ�Ȃ̂ŁA�������f�L���ŕ\���܂��B�܂��A���ʑ̂̒��ɂ́A�\��������Ȃ��̂ƕs����Ȃ��̂�����A�s����Ȃ��͎̂��Ԃ��o�߂���ƁA�O���Ɂu���ː�(radiation)�v���o���āA����Ȍ��q�ւƕω����Ă����܂��B������u���ː�����(radioactive decay)�v�Ƃ����A���̂Ƃ��ɕ��ː����o���������u���˔\(radioactivity)�v�Ƃ����܂�(���ː��̉Ȋw���Q��)�B
�\.6 ���q�j�̕��ː�����
|
���ː����� |
���q�j�̕ω� |
|
������ |
���q�ԍ���2�A���ʐ���4���������q�j�ɕω� |
|
������ |
���q�ԍ���1�傫�����q�j�ɕω� |
|
���� |
���q�ԍ��Ǝ��ʐ��ɕω��͂Ȃ� |
�s��������ː����o�����ʑ̂��u���ː����ʑ�(radioisotope)�v�Ƃ����A���ː����o���Ȃ�����ȓ��ʑ̂��u���蓯�ʑ�(stable isotope)�v�Ƃ����܂��B���ʐ���3��3H�́A��\�I�ȕ��ː����ʑ̂ł��B���q�ԍ�92�̃E����U���d�����f(���E�������f)�́A��������s��������ː����ʑ̂������܂��B�܂��A���q�ԍ�86�̃��h��Rn�E���q�ԍ�88�̃��W�E��Ra�E���q�ԍ�89�̃A�N�`�j�E��Ac�ȂǁA�������͒Z���̂�(�������Œ��̓��ʑ̂ł����ꂼ��92���ԁE1600�N�E22�N)�A�ʂ̌��f����₦�����܂�Ă�����ː����f���V�R�ɂ͂���܂��B���q�ԍ������ɑ傫����ł��Ȃ��̂ɁA�s����ȕς����̂��A���q�ԍ�43�̃e�N�l�`�E��Tc�ƌ��q�ԍ�61�̃v�����`�E��Pm�ł��B�z�q���ƒ����q���̃o�����X���������߁A�ǂ̓��ʑ̂��V�R�ɂ͑��݂ł��܂���B
(ii) ���ː����ʑ̗̂��p
���ː��͍זE������A��`�q�ɏ���t���ĕω��������肷�铭�������邽�߁A����ʈȏ�̕��ː��𗁂т邱�Ƃ͐��̂ɗL�Q�ł���A���̈����ɂ͒��ӂ��K�v�ɂȂ�܂��B�������A�\���ȊǗ����ł́A���ː��͎E�ۂ��ÁA�����̕i����ǂȂǂɗ��p�ł��܂��B�܂��A���ː����ʑ̂̏o�����ː���ڈ�Ƃ��āA���̓��̌��q�̓�����A���w�����̎d�g�ׂ݂錤�����s���Ă��܂��B
���̑��A���ʑׂ̂邱�Ƃɂ���āA�n���X�P�[���̋C��ϓ��̃��J�j�Y����m�邱�Ƃ��ł��܂��B���݂̒n���́A�n���w�I�ɐV����́u��l�I(quaternary)�v�ƌĂ�鎞��ŁA�u�X�͎���(ice age)�v�ɕ��ނ���܂��B���݂̒n�����u���g��(warm period)�v���Ǝv���Ă���l�����邩������܂��A�n���j�ɂ����ẮA�ނ��늦��Ȏ���ɕ��ނ����̂ł��B�������A���݂͕X�͎���ɂ����鉷�g���[�h�ł���u�ԕX��(interglacial period)�v�ɑ������܂��B��������̊���[�h�́u�X��(glacial period)�v�ƌĂ�Ă���A��ʓI�ɃC���[�W����u�X�͊��v�Ƃ����̂́A���̃��[�h�̂��Ƃł��B
���āA�C��͐ϕ��Ɋ܂܂�Ă���L�E���Ƃ��������̊k�Ɋ܂܂��_�f���ʑ̂̔䗦�̕��͌��ʂ���A�u�X���ƊԕX���͖�10���N�̎����ŌJ��Ԃ���Ă���v�Ƃ������Ƃ����炩�ɂȂ�܂����B�L�E���̊k�͒Y�_�J���V�E��CaCO3�łł��Ă���A���̎_�f���ʑ̔�́A�����̊C���̎_�f���ʑ̔�f�������̂ƂȂ�܂��B�C���̎_�f���ʑ̔�́A�{���C��ɂ�炸�قڈ��ł���ƍl�����Ă��܂������A�ꕔ�̊C�����������Đ�ɂȂ�A���ɐς���v���Z�X��ʂ��āA���X�ɕς���Ă������Ƃ��m����悤�ɂȂ�܂����B
�}.5 �L�E���́A�Y�_�J���V�E��CaCO3�̊k�������������ł���
�_�fO�ɂ́A���q�ʂ����Ȃ铯�ʑ̂�16O, 17O, 18O�̎O��ނ���܂��B���̂�����99%�ȏ��16O�ł��B������������ہA�d���_�f���ʑ̂��܂ސ������A�y���_�f���ʑ̂��܂ސ��̕����������₷�����߁A�C���̒Ⴂ��Ԃ������ԑ����ƁA�嗤�̓������ɐς�������̎_�f���ʑ̂́A����Ɍy���g���ɂȂ��Ă����܂��B�t�ɁA�C���ɂ͏d���_�f���ʑ̂����c����Ă����܂��B���Ȃ킿�A�C���ɏd���_�f���ʑ̂������Ƃ������Ƃ́A�嗤�ɕX�͂����B���Ă��邱�Ƃ��Ӗ����A�L�E���̊k�Ɋ܂܂��_�f���ʑ̔�͂��邱�ƂŁA�ԐړI�ɓ����̊C���̎_�f���ʑ̔�ׂ邱�Ƃ��ł���Ƃ�����ł��B���̌����ɂ��ƁA���炩��10���N�̎����ŁA�C��ϓ����J��Ԃ���Ă��邱�Ƃ����������Ƃ����܂�(�n�����g���̉Ȋw���Q��)�B

�}.6 �L�E���̊k�̎_�f���ʑ̔�ׂ邱�Ƃɂ���āA�X���ƊԕX������10���N�̎����ŌJ��Ԃ���Ă��邱�Ƃ���������
(iii) �n�[�L���X�̖@��
�@���q�ԍ��̑傫�����f�ׂĂ����ƁA�����̌��q�ԍ��������f�̑��ݗ��́A���̑O��̊�̌��q�ԍ��̌��f�̑��ݗ������A�傫���l�ɂȂ邱�Ƃ��������Ă��܂����B������u�n�[�L���X�̖@��(Harkins�f law)�v�Ƃ����A1917�N�ɃA�����J�̉��w�҂ł���E�B���A���E�n�[�L���X���A�n�k�̌��f�g���ɂ��Ă̌����Ō��o���܂����B����͌o���I�ɓ���ꂽ�@���ł������A���̌�A���q�j���̗z�q�ƒ����q�̑g�ݍ��킹�ɂ���āA���q�j�����艻����̈悪���邱�Ƃ�������܂����B���̗z�q��P�ƒ����q��N�́u���@��(magic number)�v�ƌĂ�AP��2, 8, 20, 28, 50, 82, 126�AN��2, 8, 20, 28, 50, 82, 126, 152���m���Ă��܂��B���@���𗝘_�I�ɐ��������A�����J�̕����w�҂ł���}���A�E�Q�b�p�[�g=���C���[�ƃh�C�c�̕����w�҂ł��郈�n�l�X�E�C�F���[���́A1963�N�Ƀm�[�x�������w�܂���܂��܂����B
�}.7 ���@�����ؖ������}���A�E�Q�b�p�[�g=���C���[(��)�ƃ��n�l�X�E�C�F���[��(�E)
�z�q���܂��͒����q�������@���ł��錴�q�j���u���@�j(magic nucleus)�v�Ƃ����A���ӂ̑��̌��f�ɔ�ׂāA��葽���̈��蓯�ʑ̂������Ă��܂��B�Ⴆ�A�z�q��P��50��Sn�ɂ́A10��ނ̈��蓯�ʑ̂��܂�21��ނ̓��ʑ̂����݂��܂��B�܂��A�z�q���ƒ����q�������ɖ��@�������u��d���@��(double magic number)�v�̌��q�j�́A���Ɉ��艻���邱�Ƃ��m���Ă��܂��B��d���@���������q�j�̒��ŁA�ł��d�����q�j�́A�z�q��P��82�A�����q��N��126��208Pb�ł��B
�C�����瓾���鉖�ɂ��āA�u�H��/�����i�g���E��/NaCl�v��3�̕\����������܂��B�H���́u�H�p�̉��v�Ƃ����Ӗ��ł���A�Â�����g���Ă������p���ł��B����ŁA���Ƃ�2�̖��O�́A���̕������u�i�g���E��Na�v���u���fCl�v����ł��������ł����Ƃ������Ƃ��A���炩�ɂȂ��Ă��珉�߂Ďg����悤�ɂȂ������̂ł���A������200�N�قǂ̗��j��������܂���B�����̖��O�̕\�����́A�u���p��/���w��/���w���v�ɑ���������̂ł��B����ł́A���w�ŕ����̖��O��\���Ƃ��ɂ́A�ǂ̂悤�ɕ\���̂���ԗǂ��̂ł��傤���H�Ⴆ�A�H�����uNaCl�v�Ə����ANa��Cl�̌��䂪1�F1�ł���ƕ���܂��B�������A���ꂪ�����u�����i�g���E���v�Ə�����Ă����Ȃ�A����̏��͕���Ȃ��܂܂Ȃ̂ł��B���̂悤�ɁA���w�̌��ۂ��~�N���ȃ��x�����炵������Ɨ������Ă����Ƃ��́A�uNaCl�v�ƕ\���u���w��(chemical formula)�v���ł������̏���^���Ă���܂��B���w�̗����ɂ����āA���w�����g���ĕ�����\�����Ƃ́A����I�ɏd�v�ȈӖ��������Ă��܂��B
���w���́A���w���������f�L���ŋL�q������̂ł����A���̏������ɂ͗l�X�Ȃ��̂�����܂��B�Ⴆ�A�u�g����(compositional formula)�v�́A���w�����̊e���f�̗��q������A�ł��ȒP�Ȑ�����ŕ\�����ł��B������C�I���������Ȃǂ̂悤�ɁA�������A�����ĕ������\������Ă���Ƃ��́A���w���Ƃ��Ă͂��̑g�������������܂���B����ŁA���������q����Ȃ�ꍇ�́A�u���q��(molecular formula)�v���g���܂��B���q���́A���q���ɂ��錳�f�Ƃ��̐������������ł��B�܂��A�u�\����(structural formula)�v�́A���q���ɂ����錴�q�܂��͌��q�c�̌����W��\�������ł��B���ɗL�@�������ł́A�ِ��̂������Ƃ������̂ŁA���̍\���̕\���ɍ\�����͕s���ł��B�u�d�q��(electronic formula)�v�́A���q���m�̌����Ɋ֗^����d�q���R�����u�F�v�ŕ\���������ł��B�A�����J�̕����w�҂ł���M���o�[�g�E���C�X���l�Ă������߁A�u���C�X�\����(Lewis structural)�v�Ƃ��Ă�܂��B
�\.7 ��ȉ��w��
|
���w�� |
���� |
|
�g���� |
�����̌��f�g�����ł��ȒP�Ȑ�����Ŏ������� |
|
���q�� |
���q���\�����錳�f�Ƃ��̌��q������������ |
|
�\���� |
���W�u�|�v��p���ĕ����̍\������������ |
|
�d�q�� |
���d�q�̔z�u���R�����u�F�v�Ŏ������� |
���w�ω��ɂ����āA�������镨���Ɛ����镨���̊W���A���w���Ŏ����������u���w������(reaction formula)�v�Ƃ����܂��B�Ⴆ�A���f�Ǝ_�f���������ē_����ƁA���������܂��B���̔������ɂ���ƁA���f��H2, �_�f��O2, ����H2O�ł��邩��A�܂��͎��̂悤�ɏ������Ƃ��ł��܂��B
H2�@�{�@O2�@���@H2O
�Ƃ��낪�A���w�����ł́A���q�Ԃ̌����W���ω����邾���ł���A�V���Ɍ��q�����܂ꂽ��A���q���Ȃ��Ȃ����肷�邱�Ƃ͂Ȃ��̂ŁA���̂܂܂ł͗��ӂŌ��q�̐�������Ȃ��Ȃ�܂��B�����킿�A���f���qH�͍��ӂ��E�ӂ�2�Ŗ�肠��܂��A�_�f���qO�͍��ӂ�2�A�E�ӂ�1�ɂȂ��Ă��邩��ł��B�����ŁA���ӂ̎_�fO2�̑O��1/2��t����A���q���ɂ��Ă͖�肪�Ȃ��Ȃ�܂��B
![]()
�������Ȃ���A�_�f���qO2�Ǝ_�f���qO�ł͔��������قȂ�A���w�I�ɂ͑S���̕ʕ��Ȃ̂ł��B���q���̏�ł�1/2O2��O�ł����A�����̊�{�P�ʂ̕\�����@�Ƃ����_���炷��ƁA1/2O2��O�Ƃ͂Ȃ�܂���B�_�f���q�̍ŏ��P�ʂ�O2�ł��邩��A1/2O2�Ȃ���̂͑S�����̂̂Ȃ����̂Ȃ̂ł��B���������āA���w�������ɂ����āA���w���̑O�̌W�����ŕ\�L���邱�Ƃ́A��ʓI�ɖ]�܂�������܂���B�����ŁA�S�̂�2�{���āA�����������Ă��Ǝ��̂悤�ɂȂ�܂��B
2H2�@�{�@O2�@���@2H2O
���̂悤�ɂ���ƁA���w���������������܂��B�ȏ���܂Ƃ߂�ƁA���w�������̏������́A��ʓI�Ɏ��̂悤�ɂȂ�܂��B
|
�@ �������Ɛ����������w���ŕ\���B�������A�G�}�͔������ɉ����Ȃ��B �A ���ׂĂ̌��f�ɂ��āA���ӂƉE�ӂł̌��q�������킹��悤�ɌW�������߂�B �B ���̌��ʁA�����W�����ł���A�S�̂����{�����Đ����̌W���ɂȂ�悤�ɂ���B |
�܂��A�C�I�����֗^���锽���ɂ����āA�������Ȃ��C�I�����ȗ��������w���������A���Ɂu�C�I��������(ionic equation)�v�Ƃ����܂��B�C�I���������ł́A���ӂ̓d�ב��a�ƉE�ӂ̓d�ׂ̑��a�����������Ƃɒ��ӂ��Ă��������B�Ⴆ�A�Ɏ_��AgNO3���n�t�Ɖ����i�g���E��NaCl���n�t��������ƁA�������N���ĉ�����AgCl�����a���܂��B���̉��w�ω��́A���̂悤�ɕ\����܂��B
Ag+�@�{�@Cl�|�@���@AgCl ����C�I��������
AgNO3�@�{�@NaCl�@���@AgCl�@�{�@NaNO3 ������w������
���w�ω��ł́A���ӂ́u������(reactant)�v�̗ʂɂ��A�E�ӂ́u������(product)�v�̗ʂ����܂�܂��B�����̗ʓI�W�́A���w���������狁�߂邱�Ƃ��ł��܂��B�����ŁA�������͐��f�Ǝ_�f���������Đ��������锽���ɂ����āA�u���f��W g��������Ɛ��͉�g�ł��邩�H�v�Ƃ����悤�Ȗ��ɂ悭�o��܂��B���̖����������߂ɂ́A���w������2H2�{O2��2H2O����A����������ǂݎ��Ȃ���Ȃ�Ȃ��̂ł��B���̔������̌W�����Ӗ����Ă��邱�Ƃ́A2�̐��f���q��1�̎_�f���q���������āA2�̐����q���ł���Ƃ������Ƃł��B���w�������̌W���́A�������闱�q�̐��Ɛ������闱�q�̐��̔��\���Ă���̂ł��B���w�������ɂ����āA�����������w���̌W������ǂݎ�����́A�����Ɋ֗^���闱�q�̌��̊W�����ł��邱�Ƃɒ��ӂ��Ă��������B���������āA���w�����Ŏ��ʂ������Ƃ��ɂ́A�����̌��ɊW����ʂƕ����̎��ʂɊW����ʂ̕ϊ����@���w�Ȃ���Ȃ�܂���B
(4) ���w�Ŏg�����
(i) ���q��
�e���q�̎��ʂ���10�|23 g�Ƌ��߂ď������A���̂悤�Ȕ��ɏ����Ȏ��ʂ��v�Z�ň����͕̂s�ւł��B�����ŁA��X�̌��q�̎��ʂ́A�z�q6�ƒ����q6������Ȃ����ʐ�12��12C���q1�̎��ʂ�12(�P�ʂȂ�)�������Ƃ��́u���ΓI�Ȏ��ʁv�ŕ\���܂��B����ɂ��ƁA�e���q�́u���Ύ���(relative mass)�v�́A�قڎ��ʐ��ɋ߂��l�ƂȂ�܂��B����́A�d�q�̎��ʂ͗z�q�⒆���q�̎��ʂɔ�ׂĖ����ł���قǏ������A�܂��z�q�ƒ����q�̎��ʂ��قƂ�Ǔ��������߂ł��B�Ⴆ�A1H���q1������̎��ʂ�1.6735�~10�|24 g�ŁA12C���q1������̎��ʂ�1.9926�~10�|23 g�Ȃ̂ŁA12C���q1�̎��ʂ�12�A1H���q1�̎��ʂ�MH�Ƃ���ƁA���̂悤�ɂȂ�܂��BMH��1.0078�́A1H�̎��ʐ�1�Ƃقړ����l�ł��B
1.6735�~10�|24 g �F 1.9926�~10�|23 g �� MH �F 12
�� MH��1.0078
�������A1�̌��f�ɂ́A���ʐ��̈قȂ铯�ʑ̂����݂��邱�Ƃ��������߁A���錳�f�̑��Ύ��ʂ̕��ϒl�����߂悤�Ƃ����Ƃ��ɂ́A�e���ʑ̂̑��Ύ��ʂƂ��̑��ݔ���l�����Ȃ���Ȃ�܂���B�����ŁA���錳�f�̓��ʑ̂̑��Ύ��ʂƂ��̑��ݔ䂩�狁�߂��镽�ϑ��Ύ��ʂ��A��ʓI�Ɂu���q��(atomic weight)�v�Ƃ����܂��B�Ⴆ�A���R�E�ɂ���Y�f�ɂ́A���Ύ���12��12C��98.93%�A���Ύ���13��13C��1.07%���݂���̂ŁA�Y�f�̌��q�ʂ͎��̂悤�Ɍv�Z�ł��܂��B
![]()
����āA���ʑ̂��l�������Y�f�̌��q�ʂ�12.01�ƂȂ�܂��B���̂悤�ɁA���q�ʂ͒P�ʂ̑��݂��Ȃ����Ύ��ʂ��狁�߂��l�Ȃ̂ŁA�P�ʂ̂Ȃ��ʂł��B���q�ʂ͎��ʂɊW����ʂȂ̂ŁA�P�ʂƂ���g�Ȃǂ�t�������Ȃ�܂����A�P�ʂ�t���Ă͂����܂���B���q�ʂ́A���w�v�Z�̍ۂɍł���{�I�Ȑ��l�Ƃ��ďd�v�ł��B��ʓI�Ȏ����\�ɂ́A�L������4���̐��l��������Ă��܂����A���Z�ł͓��Ɏw��������ꍇ�������āA�L������2����������3���̌��q�ʂ̊T���l�Ōv�Z���s�����Ƃ������ł��B�\.8�Ɏ�Ȍ��f�̌��q�ʂƊe���ʑ̂̑��ݔ�������܂��B�������A���q�ʂ͒ʏ���ɗ^�����Ă���̂ŁA�����Ɋo����K�v�͂���܂���B
�\.8 ��Ȍ��f�̌��q�ʂƊe���ʑ̂̑��ݔ�
|
���q�ԍ� |
���f�L�� |
���ʑ� |
���ݔ�[%] |
���q�� |
|
1 |
H |
1H |
99.9885 |
1.008 |
|
2H |
0.0115 |
|||
|
6 |
C |
12C |
98.93 |
12.01 |
|
13C |
1.07 |
|||
|
7 |
N |
14N |
99.636 |
14.01 |
|
15N |
0.364 |
|||
|
8 |
O |
16O |
99.757 |
16.00 |
|
17O |
0.038 |
|||
|
18O |
0.205 |
|||
|
11 |
Na |
23Na |
100 |
22.99 |
|
13 |
Al |
27Al |
100 |
26.98 |
|
16 |
S |
32S |
94.99 |
32.06 |
|
33S |
0.75 |
|||
|
34S |
4.25 |
|||
|
36S |
0.01 |
|||
|
17 |
Cl |
35Cl |
75.76 |
35.45 |
|
37Cl |
24.24 |
|||
|
18 |
Ar |
36Ar |
0.3336 |
39.95 |
|
38Ar |
0.0629 |
|||
|
40Ar |
99.6035 |
|||
|
19 |
K |
39K |
93.2581 |
39.10 |
|
40K |
0.0117 |
|||
|
41K |
6.7302 |
|||
|
20 |
Ca |
40Ca |
96.941 |
40.08 |
|
42Ca |
0.647 |
|||
|
43Ca |
0.135 |
|||
|
44Ca |
2.086 |
|||
|
46Ca |
0.004 |
|||
|
48Ca |
0.187 |
|||
|
26 |
Fe |
54Fe |
5.845 |
55.85 |
|
56Fe |
91.754 |
|||
|
57Fe |
2.119 |
|||
|
58Fe |
0.282 |
|||
|
29 |
Cu |
63Cu |
69.15 |
63.55 |
|
65Cu |
30.85 |
(ii) ���q�ʂƎ���
�@���f�̌��q�ʂ̘a�ɂ���āA���q1��g����1�P�ʕ��̑��Ύ��ʂ��\�����Ƃ��ł��܂��B���������ꂼ��u���q��(molecular weight)�v��u����(formula weight)�v�Ƃ����܂��B�������A���ʂ̂��Ƃ����킹�ĕ��q�ʂƂ������Ƃ�����܂��B�Ⴆ�A���q�ʂ͗L������2�����\����H��1.0, N��14, O��16, Na��23, Cl��35.5�Ȃ̂ŁA���q�ʂ�H2O��18, NaCl��58.5, NO3�|��62�ƂȂ�܂��BNO3�| �̂悤�ɓd�ׂ����ꍇ�ł��A�d�q�̎��ʂ͌��q�j�̎��ʂɔ�ׂĔ��ɏ������̂ŁA�d�q�̎��ʂ����āA�C�I���̑��Ύ��ʂ͍\�����錴�q�̌��q�ʂ̑��a�ɓ������Ƌߎ��I�ɍl����̂���ʓI�ł��B�܂��A���q�ʂƎ��ʂ����ΓI�Ȏ��ʂł��邩��A�P�ʂ�t���܂���B
�\.9 �@��ȕ����̕��q�ʂ܂��͎���
|
���� |
���w�� |
���q�ʂ܂��͎��� |
|
���f |
H2 |
2.0 |
|
���f |
N2 |
28 |
|
�_�f |
O2 |
32 |
|
�� |
H2O |
18 |
|
��_���Y�f |
CO2 |
44 |
|
�A�����j�A |
NH3 |
17 |
|
�������f |
HCl |
36.5 |
|
�Y�_ |
H2CO3 |
62 |
|
�����i�g���E�� |
NaCl |
58.5 |
|
�Y�_�J���V�E�� |
CaCO3 |
100 |
|
���_��(II) |
CuSO4 |
160 |
(iii) �A�{�K�h�����ƕ�����
���w�ł́A6.02�~1023�̗��q�̏W�c(���m�ɂ�6.02214076�~1023��)��1 mol�ƒ�`���āAmol��P�ʂƂ��ĕ\���������̗ʂ��u������(amount of substance)�v�ƌĂ�ł��܂��B�܂��A6.02�~1023�Ƃ��������u�A�{�K�h����(Avogadro constant)�v�Ƃ����܂��B���̖��̂́A���q��������C�^���A�̉��w�҂ł���A���f�I�E�A�{�K�h���̖��ɂ��Ȃ�ł��܂��B�A�{�K�h�����̋ߎ��l�́A�����}.8�̂����ɋ��߂邱�Ƃ��ł��܂��B���A���q�̑��Ύ��ʂ̊�ł��鎿�ʐ�12�̒Y�f���q12C��12 g�������悵���Ƃ��܂��B����Ɋ܂܂��12C���q�̌�N�́A12C���q1������̎��ʂ�1.9926�~10�|23 g�Ƃ���ƁA���̂悤�Ɍv�Z�ł��܂��B
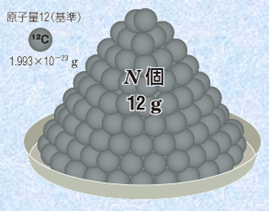
�}.8 12 g���Y�f���q12C�͉����H
12 g �F 1.9926�~10�|23 g �� N�� �F 1��
�� N��6.02�~1023��
�@mol�̒�`�́A���j�I�ɂ����ύX����āA���݂̒�`(6.02214076�~1023����1 mol�Ƃ���)�Ɏ����Ă��܂��B���݂̒�`�ɕύX���ꂽ�̂́A2019�N5��20������ł��B2018�N11���̍��ۓx�ʍt����ɂ����āA���ےP�ʌn(SI)�̊�{�P�ʂ̐V������`���A���c�E���F���ꂽ�̂ł��B�]���̒�`�ł́A�u�A�{�K�h������0.012 kg���Y�f���q12C�Ɋ܂܂�錴�q�̐��v�ƂȂ��Ă��܂������A���݂ł́u�A�{�K�h�����͌�����6.02214076�~1023�v�ƕs�m�����̂Ȃ��萔�Ƃ��Ē�`����Ă��܂��B���̒�`�̕ύX�ɂ���āAmol��kg�̒�`�Ɉˑ����Ȃ����̂ɂȂ����̂ŁA�����Ɍ����ΐ}.8�̂悤�Ȑ���������̂͐���������܂���B�������Amol�̑傫�������o�I�ɕ�����₷���A�A�{�K�h�����ɋ߂����l(�덷�͂킸��4�~10-8%)���Z�o�ł���̂ŁA���݂ł����̐���������邱�Ƃ������ł��B
�\.10 ���ےP�ʌn(SI)�̒�`�ύX
|
���ےP�ʌn |
�ύX�O |
�ύX�� |
|
������ �imol�j |
0.012 kg�̒Y�f12�̒��ɑ��݂��錴�q�̐��ɓ��������̗v�f���q���܂ތn�̕����� |
1 mol�͐��m��6.02214076�~1023�̗v�f���q���܂� |
|
�M�͊w���x �iK�j |
���̎O�d�_�̔M�͊w���x��1/273.16 |
1 K�̓{���c�}���萔k�𐳊m��1.380649�~10-23 J/K�ƒ�߂邱�Ƃɂ���Đݒ肳��� |
|
�d�� �iA�j |
�^��1 m�̊Ԋu�ŕ��s�ɔz�u���ꂽ��{�̒����̂̂��ꂼ��𗬂�A�����̓��̂̒���1 m�ɂ�2�~10-7 N�̗͂��y�ڂ��������̓d�� |
1 A�͓d�C�f��e�𐳊m��1.602176634�~10-19 C�ƒ�߂邱�Ƃɂ���Đݒ肳��� |
|
���� �ikg�j |
�P�ʂ̑傫���͍��ۃL���O��������̎��ʂɓ����� |
1 kg�̓v�����N�萔h�𐳊m��6.62607015�~10-34 J�s�ƒ�߂邱�Ƃɂ���Đݒ肳��� |
���Ȃ݂ɁAmol�̌ꌹ�̓��e����́umoles�v�ɂ���A�u�ЂƎR�́v�Ƃ��u�ЂƉ�́v�Ƃ����Ӗ��������܂��B�Ⴆ�A���q��2�~6.02�~1023�W�߂��2 mol�A���q��3�~6.02�~1023�W�߂��3 mol�ƂȂ�܂��B�܂��A1 mol������̗��q��6.02�~1023 /mol���u�A�{�K�h���萔(Avogadro constant)�v�Ƃ����A�L���uNA�v�ŕ\���܂��B
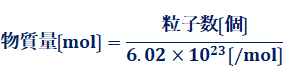
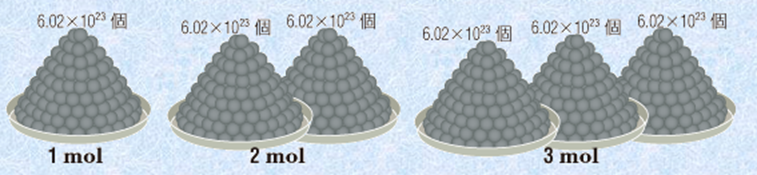
�}.9 �A�{�K�h�����ƕ�����
12C���q��6.02�~1023�W�߂��12 g�ƂȂ�̂ŁA���q�ʂ╪�q�ʂɒP�ʂƂ���g/mol��t�����u��������(molar mass)�v���悭�p�����܂��B�������ʂ́A�����̎��ʂ����̕����̕����ʂŊ��������̂ɓ������ł��B�������ʂ́A�L���uM�v���\�����Ƃ������ł��B�Ⴆ�AH2O�̕��q�ʂ�18�Ȃ̂ŁAH2O�̃������ʂ�M��18 g/mol�ƕ\���܂��B�������ʂ́A���w�ɂ����ĕ�����mol��g�̊W��^�����ƂȂ�T�O�Ȃ̂ł��B
(iv) �����v�Z
�����̕ω��́A���ׂČ��q�╪�q�Ȃǂ̏����ȗ��q���������Ƃɂ���Ĉ����N������܂��B�����āA���ʁE�̐ρE�C�̂̈��͂Ȃǂ́A���ׂė��q�̐��ɔ�Ⴗ��l�ł��B�����Ɋւ���ʂ́A��ɂ���痱�q�̐����W����̂ŁA���w�ł͗��q�����l���邱�Ƃ��ł��d�v�ɂȂ�܂��B�������A���̐���1023���x�̔��ɑ傫�Ȑ��ł���̂ŁA�ʏ��mol�Ƃ����P�ʂ��g���Č����������Ƃɂ��Ă��܂��B�Ƃ��낪�A����mol�����ǂ̂Ƃ��뗱�q�̐��ɊW����ʂȂ̂ŁA����ڑ��肷�邱�Ƃ͕s�\�ł��B�������������̗ʂő���ł���̂́A���ʁE�̐ρE�C�̂̈��͂Ȃǂł��邩��A�������g���ĕ����̗ʂ�^���邱�Ƃ������Ȃ�܂��B���������āA���̐}.10�̂悤�ȕϊ������R���݂ɂł��邱�Ƃ��A���w�̗ʂɊւ���v�Z�����������߂̑����ł��B
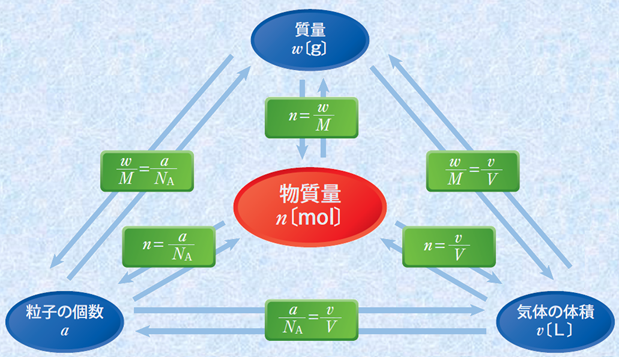
�}.10 ���w�ň����ʂ̕ϊ�
(iv-1) ���ʂƕ�����
�@�����̎��ʂƕ����ʂ̊W�́A��������(�P�ʁFg/mol)���g�����Ƃɂ���ĕϊ����邱�Ƃ��ł��܂��B�������ʂ́A������1 mol�����W�߂��Ƃ��̎���(g/mol)�ł����B�Ⴆ�A��_���Y�fCO2�̃�������44 g/mol�Ȃ̂ŁA2 mol�̓�_���Y�f�̎��ʂ�44�~2��88 g�ł��B���������āA��ʓI�ɂ͎��ʂƕ����ʂ́A���̂悤�ȊW�ɂ���܂��B
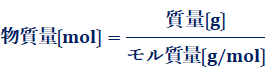
���{�ł́A�Â�����u�ڊі@�v�Ƃ����P�ʌn���p�����Ă��܂����B���݂ł́A������ł̎ڊі@�̒P�ʂ̎g�p�́A�����Ƃ��ċ֎~����Ă��܂����A�����ł����{����Ē��̔̔��́A��Ɏڊі@�̒P�ʂōs���Ă��܂��B�Ⴆ�A1�ق͖�18 mL�ł���A1���͖�180 mL�A1���͖�1.8 L�A1�l�͖�18 L�ł��B
�\.11 �@�̐ς�\���ڊі@
|
�ڊі@ |
�ϊ� |
���ےP�ʌn |
|
1�� |
10�l |
180.39 L |
|
1�l |
10�� |
18.039 L |
|
1�� |
10�� |
1.8039 L |
|
1�� |
10�� |
0.18039 L |
|
1�� |
10�� |
0.018039 L |
��H2O�̖��x��1.0 g/mL�Ȃ̂ŁA�ڊі@�ɂ��Ɛ�H2O��18 mL�W�߂��18 g�ɂȂ�܂��B��H2O�̃������ʂ�18 g/mol�Ȃ̂ŁA���傤�ǁA��1�ف���1 mol�A��1������10 mol�A��1������100 mol�A��1�l����1,000 mol�Ƃ������ƂɂȂ�܂��B�ł����������R�ł͂���܂��傤���A�ڊі@�𐧒肵���l�́Amol�����Ƃ����łɒm���Ă����̂ł͂Ȃ����Ǝv�킹��قǂł��ˁBmol�̊T�O���m�F����ۂɂ́A�v���o���Ă��������������Ƃł��B
(iv-2) �̐ςƕ�����
�����̑̐ςƕ����ʂ̊W�́A�u�A�{�K�h���̖@��(Avogadro�fs law)�v���g�����Ƃɂ���ĕϊ����邱�Ƃ��ł��܂��B�A�{�K�h���̖@���́A�u���������̉��œ��̐ς̋C�̂ɂ́A�C�̂̎�ނɊW�Ȃ������̕��q���܂܂��v�Ƃ����@���ł��B�A�{�K�h���̖@���ɂ��A���������̉��ŋC�̂̑̐ς͕����ʂ݂̂ɔ�Ⴕ�A1mol�̕��q����߂�C�̂̑̐ς́A���ׂĂ̋C�̂łقړ����ɂȂ�܂��B���x0���Œʏ�̑�C��(1atm)�̏�Ԃ��A�C�̂́u�W�����(standard state)�v�Ƃ����܂��B�C�̂̑̐ς��l����Ƃ��́A���̏�������ɂ��邱�Ƃ������ł��B
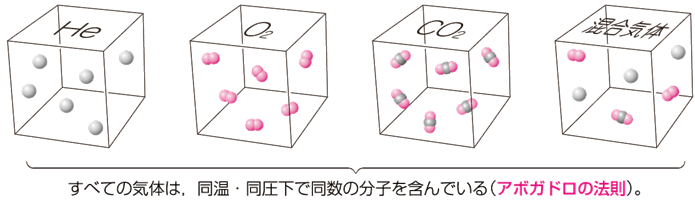
�}.11 �A�{�K�h���̖@��
���āA���ۂɑ��肵�Ă݂�ƁA�W����Ԃł͂ǂ�ȋC�̂�1 mol�ő̐ς��ق�22.4 L�ɂȂ�܂��B�܂��A���̂��Ƃ́A��C�̂悤��2��ވȏ�̍����C�̂ɂ����Ă����藧���Ƃł��B����1 mol����߂�̐ς��u�����̐�(molar volume)�v�Ƃ����A�C�̂̃����̐ς́A�W����Ԃł͂��̎�ނɊW�Ȃ��ق�22.4 L/mol�ł��B�Ⴆ�A�W����Ԃ�3 mol�̋�C�̑̐ς́A22.4�~3��67.2 L�ł��B���������āA��ʓI�ɂ͑̐ςƕ����ʂ́A���̂悤�ȊW�ɂ���܂��B

(iv-3) ���͂ƕ�����
�����̈��͂ƕ����ʂ̊W�́A�C�̂̏ꍇ�Ɨn�t�̏ꍇ�ŁA�ϊ��̎d�����قȂ�܂��B�C�̂̏ꍇ�́A�u���z�C�̂̏�ԕ�����(ideal gas law)�v��p���܂��B�������̐ς̉��ł́A�C�̂̈��͕͂����ʂ݂̂ɔ�Ⴕ�A1 mol�̕��q���^���鈳�͂́A���ׂĂ̋C�̂łقړ����ɂȂ�܂��B����́A�A�{�K�h���̖@���Ɏ��Ă��܂��ˁB���������āA��ʓI�ɂ͋C�̂̈��͂ƕ����ʂ́A���̂悤�ȊW�ɂ���܂��B���z�C�̂̏�ԕ������́A�A�{�K�h���̖@���������ՓI�ȋC�̖@���ł�(���z�C�̂̏�ԕ��������Q��)�B
�C�̂̈��́kPa�l�~ �C�̂̑̐ρkL�l�� �����ʁkmol�l�~ 8.31�~103�kPa�L/(mol�K)�l�~ ��Ή��x�kK�l
�@�܂��A�n�t�̏ꍇ�ł́A�u�Z����(osmotic pressure)�v���ʂɕϊ�������@������܂��B�Z�����́A���������u�Ăď��n�}�Ɨn�t��ڂ����Ƃ��A�n�}������n�t���ւ̗n�}�̐N�����~�߂邽�߂ɁA�n�t���ɂ�����ׂ��ߏ�̈��͂̂��Ƃł��B�Z�����ƕ����ʂ̊W�́A�u�t�@���g�z�b�t�̎�(van's Hoff formula)�v�ŕ\����܂��B��ʓI�ɐZ�����ƕ����ʂ́A���̂悤�ȊW�ɂ���܂�(�n�t���w(�n�t�̑��ꐫ)���Q��)�B
�Z�����kPa�l�~ �n�t�̑̐ρkL�l�� �����ʁkmol�l�~ 8.31�~103�kPa�L/(mol�K)�l�~ ��Ή��x�kK�l
(5) �����\
�@���f�Ƃ͈�̉��Ȃ̂��\�\��������X�́A�˂��l�߂����́A������ނ́u���q�v�̏W�܂�ł��邱�Ƃ�m���Ă��܂��B�u�S�v�Ƃ������f�́A�S���q���K���������W�����Ăł��Ă��邵�A�u�H���v�Ƃ��������́A���f�ƃi�g���E���Ƃ���2�̌��q���W�܂��Ăł��Ă��܂��B19���I�㔼�܂łɌ��f�����̓w�͂��d�˂��A���̎�ނ�50�ȏ�𐔂���悤�ɂȂ��Ă��܂����B�������A�����͈ꌩ���Ă��܂蒁���炵�����̂��Ȃ��A�����o���o���ɑ��݂��Ă���悤�Ɍ����܂����B�u����Ȃ͂��͂Ȃ��B���E�̂��Ƃł��錳�f�ɂ́A�S�̂��т����炩�̖@����������͂����v�\�\�ƍl�������w�҂́A���R�������܂����B�Ⴆ�A�C�M���X�̉��w�҃W�����E�j���[�����Y�́A���f���d�����ɕ��ׂĂ����ƁA8�Ԗڂ��ƂɎ��������̌��f������邱�Ƃ������A���K�ɂȂ��炦�āu�I�N�^�[�u�̖@���v�Ɩ��t���Ĕ��\���܂����B����́A����̖ڂ��猩�Ă����I�ȃA�C�f�B�A�ł������A�����̉��w�҂�������͒����Ƃ��ď����̂ɂȂ�A�u����ł͌��f�Ɉ�ȉ��t�����Ă���v�Ƃ��炩����n���ł������Ƃ����܂��B
1869�N2���A���������m�����܂Ƃ߂Č���ł\�����̂��A���V�A�̉��w�҂ł���h�~�g���E�C���@�m���B�`�E�����f���[�G�t�ł����B�����f���[�G�t�́A���V�A���w��ɎQ�����Ă��鑽���̉��w����1���̎����z��܂����B���̎��́u���f�̏������Ƃ��̌��q�ʂƂ̊W�v�Ƃ����_���ŁA�����f���[�G�t�́u���f�͌��q�ʂ̏��ɕ��ׂ�ƁA���w�I�����������I�Ɍ����v�Əq�ׂ܂����B�����f���[�G�t�́A���V�A��̉��w����̋��ȏ��u���w�̌����v�����M���Ă����ہA����63��ނ܂Ŕ������������Ă������f�����������@�ɔY��ł��܂����B�����f���[�G�t�́A���g���D���ȃJ�[�h�Q�[���̃\���e�B�A���甭�Ă��A���f��������������J�[�h�����x�����q�ʏ��ɕ��בւ��邱�Ƃ��J��Ԃ����ɁA1�̕\�����グ���̂ł����B�����f���[�G�t�̒�Ă����u�����\(periodic table)�v�́A�����m���Ă���63��ނ̌��f�����q�ʂ̏��������ɕ��ׁA����ɐ����̎��Ă�����̂����̗�ɕ��ׂ����̂ł���(���݂̎����\�Ƃ͏c���̎g�������t)�B
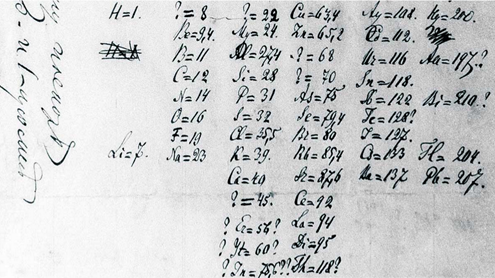
�}.12 �����f���[�G�t��1869�N2���̃��V�A���w��ŎQ���҂ɔz�z���������\�̃���
�@���f������ɓ������āA���q�ʂ���Ƃ����̂́A�����f���[�G�t���ŏ��ł͂���܂���ł����B�������A���q�ʂƗl�X�Ȍ��f�̐����Ɋւ���m����g�ݍ��킹�Ďw�W�Ɏg�����̂́A�����f���[�G�t���ŏ��ł����B����I�������̂��A���q�ʂ̏��Ԃ͋����Ă��܂��Ă��A���f�̐������画�f���Č��f�̏��Ԃ�ς��邱�Ƃ��Ƃ��ǂ��������Ƃ������Ƃł��B���f�����q�ʂɂ���Ăł͂Ȃ��A���̐����ɂ��������ĕ��ׂ邱�Ƃɂ��A19���I�Ɍ��f�����悤�Ƃ��Ă������w�҂����ʂ��Ă����傢�Ȃ���E�\�\���q�ԍ��ł͂Ȃ����q�ʂ���ɍ�Ƃ��Ă������Ɓ\�\�̉e����ጸ���邱�Ƃ��ł����̂ł��B�������Ȃ���A�������̕\�ɉ��l��F�߂鉻�w�҂́A�قƂ�ǂ��܂���ł����B���V�A�����݂̂Ȃ炸�C�O������A����ɋ^�`��������ے�I�ӌ������܂����B�������A�����f���[�G�t�́A�����ɑ��Ď����\�̈Ӌ`�J�Ɍ���Ă��܂��B�u���f�\�͋���I�ȈӋ`�������A�܂��l�X�Ȏ��������A�W�t���邱�Ƃɂ���Ă��̌��������₷�����������łȂ��A�ގ����f�����Č��f�����ɐV�������������Ƃ����_�ŏ��R����Ȋw�������v����Ɂu���܂ʼn�X�͖��m�̌��f�̐�����\�����鉽�̎�|������������A���̌��f�̂ǂꂪ����Ȃ����A���邢�͑��݂��Ȃ����𐄒肷�邱�Ƃ��ł��Ȃ������v�ƁB
�����f���[�G�t�̎����\�ɂ͂�����������܂������A�����ɂ͖�����������Ă��Ȃ����f�����Ă͂܂�͂����ƁA�����f���[�G�t�͍l���܂����B�����āA�ɓ���ׂ����f�̑��݂Ƃ��̐������A�����\�ł̏㉺���E�̌��f�̐�������\�������̂ł��B�Ⴆ�A�����f���[�G�t�́A�����\�ŃA���~�j�E���̉��Ɉʒu���関�m�̌��f���u�G�J�A���~�j�E���v�A�P�C�f�̉��Ɉʒu���関�m�̌��f���u�G�J�P�C�f�v�Ɩ��t���āA�����̐�����\�����܂����B���Ȃ݂ɁA�u�G�J�v�Ƃ̓T���X�N���b�g��Łu1�v��\���܂��B�����f���[�G�t�́A�����\�ŃA���~�j�E����1���Ƃ����Ӗ��Łu�G�J�A���~�j�E���v�A�P�C�f��1���Ƃ����Ӗ��Łu�G�J�P�C�f�v�Ƃ������O�ɂ�����ł��B
���̌�A�u�G�J�A���~�j�E���v��u�G�J�P�C�f�v�����ۂɔ�������܂����B�܂�1875�N�ɂ́A�t�����X�̉��w�҂ł���|�[���E�{�A�{�[�h�������A�s���l�[�R���ō̌@���ꂽ�����̗����z���̒�����A�K���E�������܂����B���̐�������A�����f���[�G�t���u�G�J�A���~�j�E���v�Ɩ��t���Ă����A�����\�ŃA���~�j�E���̉��Ɉʒu���関�m�̌��f�ł��邱�Ƃ�������܂����B�����1886�N�ɂ́A�h�C�c�̉��w�҃N�������X�E���B���N���[���A�A���W���_�C�g�Ƃ�����z�̒�����A�Q���}�j�E���̒P���ɐ������܂����B����́A�����f���[�G�t���u�G�J�P�C�f�v�Ɩ��t���Ă����A�����\�ŃP�C�f�̉��Ɉʒu���関�m�̌��f�ł��邱�Ƃ��m�F����܂����B�����f���[�G�t���\�����������́A�������ꂽ���f�̐����Ƃ��Ȃ�߂������̂ŁA�����f���[�G�t�̖����Ǝ����\�̒n�ʂ́A�s���̂��̂ƂȂ����̂ł��B
�\.12 �@�����f���[�G�t�̗\���Ǝ��ۂ̌��f�̔�r
|
���f |
���q�� |
���q�� |
���x |
�F |
�Z�_ |
�_���� |
������ |
|
�G�J�P�C�fEs |
72 |
4 |
5.5 g/cm3 |
�D�F |
���� |
EsO2 |
EsCl4 |
|
�Q���}�j�E��Ge |
72.6 |
4 |
5.3 g/cm3 |
�D���F |
937.4 |
GeO2 |
GeCl4 |
�����f���[�G�t�����������f��\���������ƂŁA���R�̂��ƂȂ���A���������A���疽�����悤�Ƃ������w�҂����̋������n�܂�܂����B���̌�A�M�K�X���f��A�A�[�X���f�A���ː����f�̔������������A�����\�ɓ��Ă͂܂�Ȃ��Ƃ��Ĉꎞ�͋��n�ɒǂ����܂�܂������A�M�K�X���f�ɂ͐V�����g��݂��A���A�A�[�X���f����ː����f�͐��m�Ȍ��q�ʂ����肳���ɏ]���ĕ\�ɉ����āA�����\�͊�{�I�Ȍ`��ς��邱�ƂȂ����W�������܂����B�����f���[�G�t���u���E���L����]�����v�ƌĂ����\�́A���f�̕��ނ݂̂Ȃ炸�A���w�����̓W�J�Ȃǂ��܂ށA���R�̖@����F��������ɂ߂đ傫�ȓ���ƂȂ����̂ł��B
�\.13 �����f���[�G�t���\���������f�̈ꗗ
|
�����f���[�G�t�̖��� |
���ۂ̌��f�� |
�����N |
|
�G�J�A���~�j�E�� |
�K���E�� |
1875�N |
|
�G�J�{���� |
�X�J���W�E�� |
1879�N |
|
�G�J�P�C�f |
�Q���}�j�E�� |
1886�N |
|
�G�J�e���� |
�|���j�E�� |
1898�N |
|
�G�J�^���^�� |
�v���g�A�N�`�j�E�� |
1917�N |
|
*�h�r�}���K�� |
���j�E�� |
1925�N |
|
�G�J�}���K�� |
�e�N�l�`�E�� |
1937�N |
|
�G�J�Z�V�E�� |
�t�����V�E�� |
1939�N |
* �u�h�r�v�̓T���X�N���b�g��Łu2�v���Ӗ����錾�t
�����f���[�G�t�́A�܂��m�[�x���܂��Ȃ����������1882�N�ɉp�����������A���w�̏�����ł̔��ɏd�v�Ȕ����ɑ��đ�����f�[�r�[���_�������^����Ă��܂��B����ɁA�Z�p�S�Ȏ��T�̏o�ŁA�R�[�J�T�X��h�l�c�̖��c�̒�����C���ϑ��Ȃǂ̎Y�Ƃɂ��v�����Ă������߁A1893�N�ɂ͓x�ʍt�Ǘ��Ǐ����ɏA�C���A���[�g���@�̓����ȂǁA���V�A�̒P�ʖ��̉����ɂ��w�߂܂����B�����f���[�G�t�͎����\�̋ƐтŁA1906�N�̃m�[�x�����w�܂Ƀm�~�l�[�g����܂������A�ɂ�������[���ŁA�t�b�f�K�X�̒P���ɐ��������t�����X�̉��w�҃A�����E���A�b�T���ɔs��Ă��܂�(��17�����f(�n���Q��)���Q��)�B�m�[�x�����w�܂������N�A�����f���[�G�t�͎��ӂ̂܂܁A71�ő����������܂����B72�̒a������1�T�ԑO�̂��Ƃł����B�����f���[�G�t�̑���ɂ́A��1���l���̎s�����Q�����A������26�N�O�̃h�X�g�G�t�X�L�[�̑����̎Q���҂ɕC�G����l�o�������Ƃ����܂��B
���Ȃ݂ɁA�����������̔N�͖���2�N�ɓ�����A�����f���[�G�t�Ɩ������{�ɂ́A���͐[���l�I�Ȍq���肪����܂��B�����f���[�G�t�̒��j�����W�~�[���́A�C�R���w�Z�𑲋Ƃ��ĊC�R�m���ɂȂ��Ă���A���{�̒����K��Ă���̂ł��B�����W�~�[���́A2�J�����قǒ���ɑ؍݂��Ă��܂������A�����ŏG���^�J�Ƃ������{�l�̌��n�Ȃ�������Ă��܂��B�����W�~�[���̋A����A���̓��{�l�����ɂ̓t�W�Ƃ����������܂�Ă��܂��B�����W�~�[���́A�A����6�N���33�ŖS���Ȃ��Ă��܂��܂����B�����W�~�[���̖��̉�z�^�ɂ��A�����f���[�G�t�͔ӔN�A�S���Ȃ������q�̃����W�~�[���ɑ����āA���{�ɑ������Ă����Ƃ����܂��B�^�J�ƃt�W�̐e�q�̂��̌�̏����ɂ��ẮA�悭�������Ă��܂���B���V�A�ɂ́A���łɃ����f���[�G�t���n�̎q���͂��܂���B���{�Ƀ����f���[�G�t�̎q��������\���́A���V�A�̗��j�Ƃ̊S���Ă�ł��܂��B

�}.13 �����f���[�G�t�́A�N�Ɉ�x�����U�������A�e��ȃ}�b�h�T�C�G���e�B�X�g���݂����e������
���ݎg���Ă�������\�́A���f�����q�ԍ��̏��ɕ��ׁA���́u�d�q�z�u(electron configuration)�v���l�����č���Ă��܂��B1913�N�ɁA����25�������C�M���X�̕����w�҂ł���w�����[�E���[�Y���[���A���f�����q�ʂ̏��ɕ��ׂ���A���q�ԍ�(�z�q�����d�q��)�̏��ɕ��ׂ�����A���w�I�����������I�Ɍ���邱�Ƃ�˂��~�߂��̂ł��B�����\�ɂ����āA�����s�́u����(periodic)�v�Ƃ����A�c�̗�́u��(group)�v�ƌĂ�܂��B�����\�ł́A��1�`7������7�̎����ƁA��1�`18����18�̑�������܂��B���������ɂ��錴�q�́A�ŊO�d�q�k�������ł���A�������ς��ƍŊO�k���ω����܂�(��1������K�k�A��2������L�k�A��3������M�k���)�B�܂��A�������ɑ����錳�f�́A�u�������f(congener)�v�ƌĂ�A���d�q���������ł��邽�߁A���w�I�������ގ����Ă��܂��B���̂悤�ɁA�����\�ɂ����ĕ����I�����≻�w�I�����������I�ɕω����邱�Ƃ��A�u������(periodic law)�v�Ƃ����܂��B
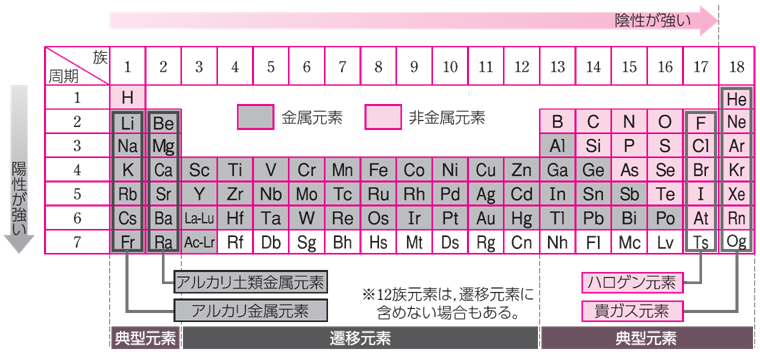
�}.14 ���ݎg���Ă�������\
���f�̎������ɂ悭�]��1����2���A�����13�`18���̌��f���u�T�^���f(typical elements)�v�Ƃ����A�������f�Ɣ�������f���قڔ������܂܂�܂��B�T�^���f�̉��d�q���́A���ԍ���1���ʂ̐��ƈ�v���܂��B�Ⴆ�A2���ł���Ή��d�q����2�ŁA15���ł���Ή��d�q����5�ƂȂ�܂��B�������A18�����f�͈�ʓI�ɉ��w���������Ȃ��̂ŁA��O�I�ɉ��d�q����0�Ƃ��܂��B���̂��߁A�T�^���f�̓������f�ł́A���f���m�̉��w�I�������悭���Ă��܂��B���ɂ悭�����������f�͌ŗL�����t���Ă���A���fH�ȊO��1�����f���u�A���J������(alkali metals)�v�A�x�����E��Be�ƃ}�O�l�V�E��Mg�ȊO��2�����f���u�A���J���y�ދ���(alkaline earth metals)�v�A17�����f���u�n���Q��(halogens)�v�A18�����f���u�M�K�X(noble gas)�v�Ƃ����܂�(��1�����f(�A���J�������Ȃ�)�A��2�����f(�A���J���y�ދ����Ȃ�)�A��17�����f(�n���Q��)�A��18�����f(�M�K�X)���Q��)�B
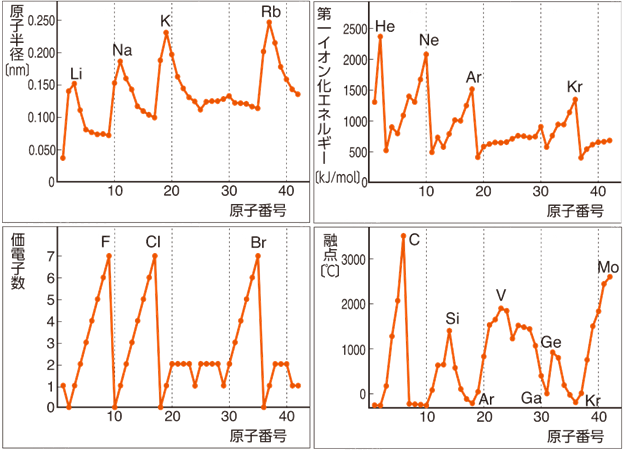
�}.15 ���f�̎�����
����ŁA�����\�̒������Ɉʒu���Ă���3�`12���̌��f���u�J�ڌ��f(transition element)�v�Ƃ����A���̂��ׂĂ��������f�ł��B�J��(transition)�Ƃ́A�u�����\�̍����ƉE���̓T�^���f���Ȃ��v�Ƃ����Ӗ��ł��B�J�ڌ��f�ł́A���q�ԍ��̑����ɔ����đ�������d�q���A�ŊO�k�ł͂Ȃ����k�ɔz�u����Ă����̂ŁA���q�̍ŊO�k�d�q�̐����A�ʏ�1�`2�ł��܂�ω����܂���B���̂��߁A�����\�ŗׂ荇�����f���m�ŁA�݂��ɉ��w�I�������悭���Ă��邱�Ƃ������ł��B�܂��A�ʏ�����\�̗��O�ɒu����邱�Ƃ��������q�ԍ�57�`71�̌��f���u�����^�m�C�h(lanthanoids)�v�A���q�ԍ�89�`103�̌��f���u�A�N�`�m�C�h(actinoids)�v�Ƃ����܂��B�����^�m�C�h�͍H�ƓI�ɗL�p���u��y�ތ��f(rare earth element)�v�ł���A�A�N�`�m�C�h�͕��˔\�������ː����f�ł��B
(6) ���w�j
�u�B���p(alchemy)�v�Ƃ́A���l�̒Ⴂ�u�ڋ����v����A���l�̍����u�M�����v�B���悤�Ƃ��鎎�݂̂��Ƃł��B�B���p�̋N���́A�Ñ�M���V�A��Ñ�G�W�v�g�ɋ��߂��܂��B3���I���ɃG�W�v�g�ŏ����ꂽ�Ǝv����╨�ɂ́A�u�����ɕʂ̋����������đ��ʂ�����@�v���L�q����Ă����Ƃ����܂��B�Ñ�G�W�v�g�̘B���p�́A�M���V�A�̏��w�ƂƂ��ɃA���r�A�����ɓ`���܂����B�����āA���̃C�X�����B���p���A����̎����I���w�̌��^���������邱�ƂɂȂ�܂��B�B���p�́A�����̖ڕW��B�����邱�Ƃ͂ł��܂���ł������A���w�I�ȕ��̍l������Z�p�́A�����̃��[���b�p�Ɉ����p����A�u���w(chemistry)�v�Ƃ��Ĕ��W���܂����B�p��ʼn��w���Ӗ�����uchemistry�v�̌ꌹ�́A�p��ŘB���p���Ӗ�����ualchemy�v�ɗR�����܂��B�����āA17���I�ɂ̓C�M���X�̃��o�[�g�E�{�C���A18���I�ɂ̓t�����X�̃A���g���[�k�E���{�A�W�G�A19���I�ɂ̓C�M���X�̃W�����E�h���g���炪�A�u�������ʂ≻�w�ω��ɂ�����ʓI�W�̗��_�v���m�����Ă����܂����B

�}.16 �B���p�̎��s�̉ߒ��ŁA���_H2SO4��Ɏ_HNO3�Ȃǂ̗l�X�ȉ��w��i���������ꂽ
����܂ł̉��w�͂Ƃ����ƁA�l�X�ȕ����̍\���E�����E�����ׂ邽�߂ɁA������ώ@�������J��Ԃ��āA�f�[�^��ςݏd�˂邾���Ƃ������̂ł����B�����̉��w�́A�܂��ɈËL�ƌo�����̊w�₾�����̂ł��B�������A�ʓI�W�̗��_���m������Ă���A�u�o�����̉��w�v�͏I���A�u�ߑ�̉��w�v�܂ŋ}���ɔ��W���Ă��܂����B����ł́A�ʎq���w�≻�w�����_�Ȃǂ��i�����āA�����̋����ɂ��āA������x�̗\���͂ł���悤�ɂȂ�܂����B�������Ȃ���A�܂��܂����w�ɂ͕���Ȃ����Ƃ���������܂��B�u������Ε�����قǕ�����Ȃ����Ƃ��o�Ă���v�\�\���ꂪ���w�Ȃ̂ł��B

�}.17 ��{�@���̗��j�I����
(i) ���ʕۑ��̖@��
�Ⴆ�A�g�߂ȉ��w�����ł���R�Ăɂ��čl�@����ƁA�⎆�͔R�₷�ƊD�ɂȂ��āA���ʂ��啝�Ɍ������܂��B�܂��A�M�C���Ɍ�����悤�ɁA�C�͔̂M����ƌy���Ȃ�悤�Ɋ������܂��B�������w�ω���ǂ��Ă���҂ɂƂ��āA���̕ω��̊O�ʓI�Ȏp�ɂ���ڂ��s�������ɂȂ邽�߁A18���I���܂ł́A���w�ω��ɔ����ʂ̎��x�𑪒肵�悤�Ƃ���l�����͂Ȃ��Ȃ��o�Ă��܂���ł����B�����������ŁA��C������ɓ���ĉ��w�������l���A���m�ȗʂ̑����ʂ��āA���������o�����Ƃ����̂��A�t�����X�̉��w�҂ł���A���g���[�k�E���{�A�W�G�ł����B

�}.18 ���{�A�W�G�͗l�X�ȉ��w�Ɋւ���Ɛт���A�u�ߑ�Ȋw�̕��v�Ə̂����
��C������ɓ���邽�߂ɂ́A��C�����Ȃ����Ƃ��d�v�ł��B���{�A�W�G�́A���g���g(����̗e��̏�ɒ������тꂽ�ǂ����Ɍ������ĐL�тĂ���K���X���̗e��)�ɃX�Y�����Ė������A�����ԋ��M���܂����B����ƁA�X�Y�̕\�ʂ͋P�����Ȃ��Ȃ�A����������̎_���X�Y�ɂȂ�܂��B�����̑O��Ŏ��ʂ̕ω��ׂĂ݂�ƁA�����ꂽ���g���g���̑S���ʂ́A�S���ω����Ă��܂���ł����B��p��Ƀ��g���g���J������ƁA���𗧂Ăċ�C�����g���g���ɗ��ꍞ�݂܂����B���ʂ𑪒肷��ƁA�n�߂̃X�Y�����A�_���X�Y�͏d���Ȃ��Ă��܂����B�d���Ȃ��������A���ꍞ��C�̏d���������̂ł��B���{�A�W�G�́A���̌��ʂ���u��������C�̈ꕔ�ł���_�f�Ɖ������āA�����_�������ł���v�ƍl���A���̗��_��R�Ĕ�����ʂɍL���čl���Ă����܂����B
���{�A�W�G�ɂ���āA�R�ĂƂ́u�R���镨���Ǝ_�f�̌��т��ł��邱�Ɓv�����炩�ɂ���܂����B�����A�R�Ăɂ��Ắu�t���M�X�g����(phlogiston theory)�v���嗬�̍l�����ŁA������R�Ă�����Ɓu�t���M�X�g���v�Ƃ������f�����o����邽�߁A���ʂ��y���Ȃ�ƍl�����Ă��܂����B���{�A�W�G�̎����́A�t���M�X�g������ے肷����̂ł����B���{�A�W�G�́A���̂��Ƃ����̔����ɂ��Ă���������̂��ǂ�����m�邽�߁A�����玟�ւƎ������d�˂܂����B�����Đ��ɁA�u���w�����̑O��ŁA�����̎��ʂ̑��a�͕ω����Ȃ��v�Ƃ����u���ʕۑ��̖@��(law of conservation of mass)�v��1772�N�Ɋm�������̂ł��B���w�̑���v���s���A�ߑ㉻�ւƓ����d�����������Ƃ���A���{�A�W�G�́u�ߑ㉻�w�̕��v�ƌĂ��悤�ɂȂ�܂��B���{�A�W�G�͐��U�Ő������̎������s���A18���I�̒i�K��33�̌��f�����Ă����Ƃ����܂��B

�}.19 �_���X�Y�����������g���g���J������ƁA���ʂ���������
�������A���{�A�W�G�̍Ŋ��͔ߎS�Ȃ��̂������B���{�A�W�G�͗T���Ŏ��Y���\���Ɏ����Ă���A���������������������ɂ��ւ�炸�A����������p�����Y����͏o�����A�����̎��Y��L���ɉ^�p���悤�ƁA1768�N�����s������ŋ�����藧�Ă钥�Ő����l�̎d���ɏA���Ă����̂ł��B�u���{�A�W�G�ɂƂ��āA�����Ƃ͓��y�ł���v�ƕ����w�҂̏��R�c���͏q�ׂĂ���A�T��1���͎����ɂӂ���A���{�A�W�G�͂��̓����u�K����1���v�ƌĂ�ł��܂����B�Ƃ��낪�A1789�N�Ƀt�����X�v���̉��N���N����ƁA���쑱���ŋQ�����s�����\�k�Ɖ����A���{�A�W�G�ɂ��댯������܂����B�������|��A���C16����}���[�E�A���g���l�b�g�Ȃǂ̉������������X�ɏ��Y����钆�A���{�A�W�G���������瑽�z�̐ŋ�����藧�Ă��Ƃ��āA���Y����邱�ƂɂȂ��Ă��܂��܂����B���{�A�W�G�̏��Y�ɂ͑����̉Ȋw�҂������A���{�A�W�G�̎��ɍۂ��āA18���I�ő�̐��w�҃��C�E���O�����W���Ɂu�ނ̓���藎�Ƃ��͈̂�u�����A�ނƓ������]�����҂������܂łɂ�100�N�͂����邾�낤�v�ƌ��킵�߂܂����B
1794�N5��8���ߑO10���A���{�A�W�G�͊v���@��Ɉ�������o����A�v�����{�͎��Y�����������n���܂��\�\�u�䂪���a���͉Ȋw�҂Ȃǂ�K�v�Ƃ��Ă��Ȃ��v�ƁB���̓���18��15���A���{�A�W�G�̓R���R���h�L��ɘA�s����A�f����M���`���ɂ������܂����B���{�A�W�G�̓M���`���ŏ��Y�����ۂɁA���Y��̐l�Ɉӎ�������̂����������邽�߁A�u�M���`���ŏ��Y����Ď����̎�������A�ӎ������邩�ǂ��������Ă��Ă���v�Ǝ��͂̐l�ɗ������ł��B���{�A�W�G�́u���������̈ӎ����������玩���͂��̎���������B�b�����Ƃ͂ł��Ȃ��Ă��ڂō��}����B�����Ă���\�Ȍ���܂����𑱂���v�Ɛ錾���܂����B�����ď��Y�̓����A�M���`���Ŏ��藎�Ƃ��ꂽ���{�A�W�G�́A���ۂɉ��܂��������������ł��B�������A�l�͎�𗎂Ƃ����Ƌ}���Ɍ�����������A�����Ɉӎ����Ȃ��Ȃ�ƍl�����Ă��邽�߁A���̘b�͂ǂ��܂Ŗ{���Ȃ̂�������܂���B

�}.20 ���{�A�W�G�̓M���`���ŏ��Y���ꂽ���ƁA���Y��̐l�Ɉӎ�������̂������������Ƃ���
���ʕۑ��̖@���́A20���I�����܂ʼnȊw�҂����̊ԂŎx�����ꑱ���Ă��܂����B�������A1905�N�Ƀh�C�c�̕����w�҂ł���A���x���g�E�A�C���V���^�C���́A���ꑊ�ΐ����_�̋A���Ƃ���E��mc2�Ƃ�����������A���ʂ̓G�l���M�[�Ɠ����W�ɂ���Ƃ������Ƃ���܂����B����ɂ��ƁA�j�Z�������ȂǂŎ��ʂ���������ƁA�傫�ȃG�l���M�[����������Ƃ����̂ł��B�Ⴆ�A�L���ɓ������ꂽ���q���e�Ŋj������N�������̂���50 kg�̃E����235�ł����A������ɂ͖�0.7 g�̎��ʂ��G�l���M�[�ɕς���āA���ʂ����������ƍl�����Ă��܂��B�����x��c��3.0�~108 m/s�Ƃ���ƁA���������G�l���M�[�͎��̂悤�ɋ��߂��܂��B
E �� 0.7�~10�|3 �~ (3.0�~108)2 �� 6.3�~1013 J
����ŁA���i�������̐g�̉��ŋN�����Ă��鉻�w�����ł́A�ǂ̒��x�̎��ʂ̑���������̂ł��傤���H�Ⴆ�A�K�\������1 L�R�₷��3.4�~107 J�̔M�ʂ����o����܂����A�����E��mc2�ɑ������ƁA���ʂ�m��3.8�~10�|7 kg�ƂȂ�܂��B�܂�A�K�\���������r�C�K�X�̕����A3.8�~10�|7 kg�����y���Ƃ������ƂɂȂ�܂��B���̂悤�ɁA�������̐g�̉��ŋN���鎿�ʕω��͂����킸���Ȃ̂ŁA��ʓI�ɂ͎��ʕۑ��̖@���͐��藧�ƍl���ėǂ��Ƃ������ƂɂȂ�܂��B
(ii) ����̖@��
���{�A�W�G�̎���A���ʂ��͂��߂Ƃ��āA�����̑O��Ő��m�ȗʂ𑪒肷�邱�Ƃ��A���w�̕���ɂ����Ĕ��ɑ�ł���ƔF������n�߂Ă��܂����B�܂��A�_A�Ɣ������鉖��B�̎��ʔ䂪�A��Ɉ��ł���Ƃ������Ƃ����炩�ɂ���܂����B���̂悤�Ȃ��Ƃ��A���w�����ɂ����Ă����ƈ�ʓI�ɐ��藧�̂ł͂Ȃ����ƌ������n�߂��l���A�t�����X�̉��w�҂ł���W���[�t�E�v���[�X�g�ł��B
����A�ƕ���B���������ĕ���C���ł���Ƃ��AA��B�͈��̔䗦�Ŕ������A���̔䗦��C��^���܂��B�Ⴆ�A���f�Ǝ_�f���������Đ�����������Ƃ��A���f1 g���_�f8 g�Ɣ������Đ�9 g���������܂����A���f1 g���_�f10 g�Ɣ������Đ�11 g����������Ƃ������Ƃ́A�����ċN����܂���B���f1 g�Ǝ_�f10 g�������悤�Ƃ���A���f1 g���_�f8 g�Ɣ������Đ�9 g���������A�_�f2 g���]��܂��B���̂悤�Ȏ������A�v���[�X�g�͗l�X�Ȕ����Ŏ����܂����B

�}.21 �v���[�X�g�́A�����������f�̐�����̑g�ݍ��킹�łł��Ă���Ƃ����T�O���L�߂����ƂŒm����
�������A�����ł͂܂��������Ɖ������̈Ⴂ�����m�ɋ�ʂ���Ă��Ȃ��������߁A���̌����͍�����ɂ߂܂����B�������̏ꍇ�ł́A�����䂪�ς��ƍ\�����f�̎��ʔ䂪�ς�邩��ł��B�������A���̐܂������𑽂��̕����ɂ��čs���A�v���[�X�g�́u�������̍\�����f�̎��ʔ�́A�������̍����ɂ�炸��Ɉ��ł���v�Ƃ����u����̖@��(law of definite proporiton)�v��1799�N�ɒ��܂����B
(iii) �{�����̖@���ƌ��q��
����̖@���́A��̉����Ӗ�����̂ł��傤���H�������fA�ƌ��fB���A�C�̂̂悤�ȃt���t�������s��`�ł���Ȃ�AA��B���K���C�ӂ̐�����ō����荇���Ƃ�������̖@���́A�����������������ł��B���ʔ䂪��Ɉ��ł���Ƃ������Ƃ��������ɂ́A�u���f�͂�����̎��ʂ��������s���̗��q����ł��Ă���v�ƍl����A���������₷���Ȃ�܂��B����ɁA����̖@���������߂ɂ́AA��B�̌��q�͂����܂�������ł̂�������ƍl���Ȃ��Ă͂Ȃ�܂���B�ȏ�̂悤�Ȑ��_����A1803�N�ɃC�M���X�̉��w�҂ł���W�����E�h���g���́A�����́u���w�N�w�̐V�̌n�v�̒��ŁA�����Ƃ��Ď��̂悤�ȁu���q��(atomism)�v����܂����B
|
�@ �����͂���ȏ㕪���ł��Ȃ������q����Ȃ�A���̔����q�����q�ƌĂ� �A �e���f�ɌŗL�̎��ʂ���������q�����݂��� �B ���w�ω��͌��q�̑g�݊����ł����āA���q���Ȃ��Ȃ邱�Ƃ������邱�Ƃ��Ȃ�(���ʕۑ��̖@���̐���) �C �������͐������f�̌��q�����̊����Ō������Ăł��Ă���(����̖@���̐���) |
���̌��q���́A���ʕۑ��̖@���ƒ���̖@���������I�ɐ������܂����B�������A������Ƃ����ĒN���������Ƃ̂Ȃ��u���q�v�����݂���Ƃ������̐����A�����̉��w�҂����͑f���Ɏ���邱�Ƃ��ł��܂���ł����B�����ł́A���𑜓x�̓��ߌ^�d�q������(TEM)����^�v���[�u������(SPM)���g���āA���q�ځu����v���Ƃ��ł��܂����A�����͌��q�̑��݂�l�X�ɔ[��������͔̂��ɍ���ł����B
���̌��q�����������Ǝ��ł���؋��͉����Ȃ����̂��ƁA�h���g���͓���Y�܂��܂����B�Ȃ��A�h���g���͌��q���u����ȏ㕪���ł��Ȃ������q�v�ƍl���Ă��܂������A����͎����Ƃ͈قȂ�܂��B���q�͌��q�j��d�q�ɕ������邱�Ƃ��ł��܂����A���q�j������ɗz�q�⒆���q�ɕ����ł��邩��ł��B���q�̏ڍׂȍ\��������������́A1911�N�̃C�M���X�̕����w�҃A�[�l�X�g�E���U�t�H�[�h�ɂ�錴�q�j�̔�����҂��Ȃ���Ȃ�܂���B

�}.22 �h���g���͌��q����������ƂŒm���Ă���
�Ƃ���ŁA���̌��q���́A���qA�ƌ��qB���ǂ̂悤�Ȋ����Ō�������̂��Ƃ������Ƃ��A�������Ă��܂���ł����B�����ŁA�h���g���͎v�����āA���R�̍��{�̓V���v���ɈႢ�Ȃ�����A�u��{�I��1�F1�̊����Ō�������v�ƌ�����܂����B�������A���ׂẲ��������A1�F1�̊����Ō������Ă����ł͂���܂���B�����A�_����(I) Cu2O�Ǝ_����(II) CuO�̂����ɁA2���ނ̌��f����Ȃ鉻�����Ŋ������قȂ镨�����������m���Ă����̂ŁA�u��O�I��1�F2�Ƃ�2�F3�Ȃǂ̔������v�ƌ����܂����B�����̎_�����́A���f�K�X���Ҍ�����Ɠ��ɂȂ�̂ŁA�����O�̎_�����̎��ʂ��甽����̓��̎��ʂ������A�_�������̎_�f�̎��ʂ������܂��B
�\.14 ��莿�ʂ̓��Ɖ�������_�f�̎���
|
|
�_����(I) |
�_����(II) |
|
�����O�̎��� |
0.90 g |
1.00 g |
|
������̎��� |
0.80 g |
0.80 g |
|
�_�f�̎��� |
0.10 g |
0.20 g |
���̂悤�Ɉ�莿�ʂ̓��Ɖ�������_�f�̎��ʂ�0.10 g��0.20 g�ł���A1�F2�Ƃ����ȒP�Ȑ�����ɂȂ�܂��B�����āA�h���g���͂��̂悤�Ȑ�����ɂȂ鉻���������ɂ�����͂��ł���Ɨ\�����A������u�{�����̖@��(law of multiple proportion)�v�Ɩ��t���܂����B���̗\���͌����ɓI�����A���̂��Ƃɂ���āA���q����M����l����������悤�ɂȂ����̂ł��B�{�����̖@���́A����̖@���Ǝ��Ă��ĕ���킵���@���ł����A����̖@���Ƃ̈Ⴂ�́A����̖@���́u1�̉������̎��ʔ�v�ɒ��ڂ��Ă���̂ɑ��āA�{�����̖@���́u2�ȏ�̉������Ԃ̍\�����q�̎��ʔ�v�ɒ��ڂ��Ă���Ƃ���ł��B�܂�A�{�����̖@���́A���q�̑��݂𗠕t��������̂ł������̂ł��B
(iv) �C�̔����̖@��
1800�N��̏��߂ɂ́A�������ꂽ�C�̂̎�ނ������Ȃ�A�����̐������L�����������悤�ɂȂ�܂����B�������A���̒��ɂ͋C�̊Ԃ̔����������̑ΏۂɂȂ��Ă��܂����B�������A1808�N�Ƀt�����X�̉��w�҂ł���W���Z�t�E�Q�[�����T�b�N�́A�u�C�̊Ԃ̔����ł́A��������C�̂���ѐ�������C�̂̑̐ϔ�́A���������̉��ŊȒP�Ȑ�����ɂȂ�v�Ƃ����u�C�̔����̖@��(law of gaseous reaction)�v����܂����B

�}.23 �Q�[�����T�b�N�̓A���R�[���Ɛ��̍����ɂ��Ă��������A�A���R�[���x���̂��Ƃ��u�Q�[�����T�b�N�x���v�ƌĂԂ��Ƃ�����
�Q�[�����T�b�N�͐����Ȏ������s���A���f�K�X�Ǝ_�f�K�X���������Đ����C���ł���ꍇ�A�u�������鐅�f�F��������_�f�F�������鐅���C��2�F1�F2�v�Ƃ��������䂪�������邱�Ƃ������܂����B�C�̔����̖@���́A�����̍ŏ��P�ʗ��q�ł��錴�q�����݂���Ƃ����h���g���̌��q�����x��������̂ƁA�����͍l�����Ă��܂����B�������A�h���g�����g�͂��̖@����F�߂Ȃ������̂ł��B
(v) ���q���ƃA�{�K�h���̖@��
�h���g���́A�Q�[�����T�b�N�̋C�̔����̖@����F�߂܂���ł����B�Ȃ��Ȃ�A�h���g���͎��R�̍��{�̓V���v���ɈႢ�Ȃ�����A���q���m�͊�{�I��1�F1�Ō���������Ⴂ�Ȃ��ƍl���Ă�������ł��B�h���g���́A���f��_�f�Ȃǂ̒P�̋C�̂́A���R1���q����Ȃ�ƍl���Ă��܂����B���̂悤�Ɍ��_�t�����h���g���́A�Ⴆ�ΐ���HO�A�A�����j�A��NH������ȂǁA������ʓI�ȕ����ɑ��āA��������w���𐄒肵�Ă��܂��܂����B����āA�����C�̐��������ɂ��āA�h���g���̎咣�����w�������Ŏ����ƁA���̂悤�ɂȂ�܂��B
H�@�{�@O�@���@HO
����ł́A�u�������鐅�f�F��������_�f�F�������鐅���C��1�F1�F1�v�ƂȂ�A�Q�[�����T�b�N�̋C�̔����̖@���Ɩ����������܂��B�����ŁA���̂悤�Ȗ������������A�C�̔����̖@������肭�������邽�߂ɁA�C�^���A�̕����w�҂ł���A���f�I�E�A�{�K�h���́A1811�N�Ƀt�����X�̊w�p�G���Ɏ��̂悤�ȁu���q��(molecular theory)�v������܂����B�����A�A�{�K�h���͊C�O�ł͑S���̖����ł����B�ŏ��͖@���ƂɂȂ邽�߂ɋ���@�Ɋւ���_���Ŕ��m�����擾���A���̂��ƂɓƊw�Ő��w�ƕ����w���C�߁A�g���m��w�ŗ��_�����w�̏��㋳���ɂȂ����ٍ˂ł����B
|
�@ �C�͉̂����̌��q�������������q����Ȃ� �A ���������œ��̐ς̋C�̂́A��ނɊW�Ȃ������̕��q���܂�(�A�{�K�h���̖@��) |
�ȏ�̂��Ƃ���A�A�{�K�h�����l���鐅���C�̐��������́A���̂悤�ɂȂ�܂��B
2H2�@�{�@O2�@���@2H2O
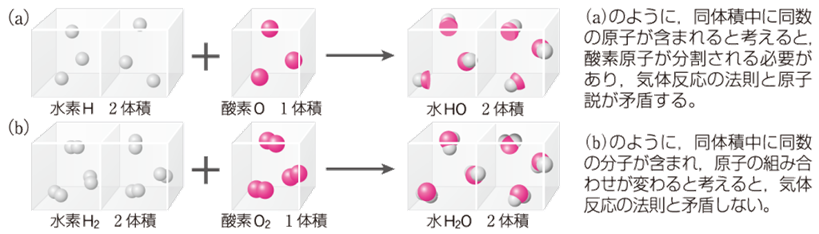
�}.24 �A�{�K�h�����l���鐅���C�̐�������
����Łu�������鐅�f�F��������_�f�F�������鐅���C��2�F1�F2�v�ƂȂ�A�Q�[�����T�b�N�̎������ʂ������ɐ����ł��܂����B�A�{�K�h���̕��q���́A�C�̔����̖@�����Ȃ���������f���炵����Ăł������̂ł��B�܂��A���ꂪ�������Ȃ�A���q�ʂ̐��m�Ȓl������ł���Ƃ������ڂ��ׂ����̂ł����B
�}.25 �A�{�K�h���������A�{�K�h���̖@���́A���Z���w�ł͕K���w�K����d�v�@���ł���
�������A�A�{�K�h���̕��q�����L���x�������悤�ɂȂ����̂́A����Ă���49�N���1860�N�̂��ƂŁA�A�{�K�h���̎��ォ��4�N���o�߂��Ă��܂����B19���I�O���A���w�̒��S�n�̓C�M���X�A�h�C�c�A�X�E�F�[�f���ł����B�C�^���A�͉��w�̌�i�����ƌ��Ȃ���Ă����̂ŁA�A�{�K�h���̘_���͒����Ԗ�������Ă����̂ł��B�A�{�K�h���̕��q���ɒ��ڂ��W�܂�_�@�ƂȂ����̂́A1860�N�Ƀh�C�c�̃J�[���X���[�G�ŊJ�Â��ꂽ���ۉ��w�҉�c�ł��B�����Ō��q�ƕ��q�̋�ʂ����c���ꂽ�Ƃ��A�C�^���A�̗L�@���w�҂ł���X�^�j�Y���I�E�J�j�b�c�@�[���ɂ���āA�A�{�K�h���̘_�������グ��ꂽ�̂ł��B�A�{�K�h���̕��q�����]������Ȃ��������R�Ƃ��Ă��A���q�����q���`�����闝�R����������Ȃ��������Ƃ�A�u�����������œ��̐ϒ��ɓ����̋C�̗��q���܂܂�Ă���v�Ƃ��������̐��낪�A��肭���ł��Ȃ��������ƂȂǂ��l�����܂��B�A�{�K�h�����@���E�̏o�g�̂ɁA�_���̕��͂�����ł��������Ƃ�����Ƃ���Ă��܂��B
�E�Q�l����
1) �A���E���[�j�[��/���،������u���f���猩�����w�Ɛl�ނ̗��j�v�V�i�m���(2019�N���s)
2) �ΐ쐳���u�V���n�̉��w(��)�v�x�䕶��(2005�N���s)
3) �m���g�f����w�̐V������O�ȓ�(2013�N���s)
4) ����́u�����f���[�G�t�Ǝ����������v���w�Ƌ���63��2��(2015�N)
5) ꎓ���/������/�R�{����/��19���u���w��b�v�[�ъ�(2012�N���s)
6) ����O�u���f118�̐V�m�� �����ďd��A�ǂ�ł������낢�v�u�k��(2017�N���s)
7) ����O�u�����f���[�G�t�̌��f�����\�a��150�N�v���w�Ƌ���67��6��(2019�N)
8) �|���O�u�|���Ė���Ȃ��Ȃ�Ȋw�vPHP������(2012�N���s)
9) �D�R�M���u���킭�Ȃ��L�@������������v�Z�p�]�_��(2014�N���s)
10) �R���K�v�u���Ȃ��������낭�Ȃ�12�b�v��g���X(2001�N���s)
11) �n�Ӑ�/�k�����F �����u���Z�ŋ���肽���������w�v���{�]�_��(2008�N���s)