・理想気体の状態方程式
【目次】
(1) 気体とは何か？
気体粒子は、「熱運動(thermal motion)」によって空間を激しく動き回っており、構成粒子間の距離が非常に大きいです。そのため、気体のほとんどは空間であり、固体や液体に比べて、密度が非常に小さいです。熱運動によって粒子が広がっていく現象は、「拡散(diffusion)」と呼ばれます。気体粒子の熱運動の運動エネルギーと温度には、密接な関係があります。例えば、気体状態の単原子分子の平均の運動エネルギーは、次の式で示されるように、絶対温度Tに比例します。ここで、kはボルツマン定数と呼ばれる定数で、k＝1.38×10−23 J/Kという値です。この式は、気体粒子の平均の運動エネルギーが、気体の圧力や体積に関係なく、絶対温度Tだけに比例するということを示しています。
次の図.1に、気体分子の運動エネルギーと温度の関係を示しました。このように、気体粒子が取り得るエネルギー準位による分布を示したグラフは、「マクスウェル・ボルツマン分布(Maxwell-Boltzmann distribution)」と呼ばれています。この曲線の極大は、その運動エネルギーを持つ気体粒子の割合が、最も大きいことを示します。ボルツマン分布より、温度が高いほど、大きな運動エネルギーを持つ気体粒子の割合が増加し、より速く気体粒子が動き回っていることが分かります。
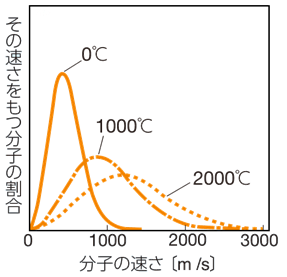
図.1 窒素分子N2の速さと温度の関係
気体のほとんどが空間であるのにも関わらず、ある体積を保つことができるのはなぜでしょうか？これは、気体粒子間の分子間力によって集合しようとする勢いに負けないだけの運動エネルギーを持って構成粒子が飛び回り、内壁に当たって押し返しているからです。容器内の気体粒子は、内壁と衝突を繰り返し、内壁に圧力を及ぼしているのです。
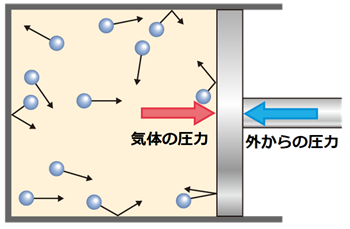
図.2 気体粒子の衝突の様子
「空気は重さを持ち、圧力を及ぼしている」といえば、今では誰でも「当たり前ではないか」というでしょう。しかし、これはわずか三百数十年前に誕生した、比較的新しい考えなのです。それ以前の人たちは、「自然は真空を嫌うので、物質は隙間のない連続体でできている」という、古代ギリシアの大哲学者アリストテレスの説を後生大事に守って、大気圧によって生じる現象をすべてこの考えで説明しようとしていました。17世紀になると、科学で現象のもとになっている原因は何かという点に目を向け、その原因を実験によって明らかにしようとする態度が生まれてきました。また、科学技術が発達してくると、実際にアリストテレスの説では、説明の付かない現象も数多く現れてきました。
揚水ポンプの現象が、その一例です。この頃、金属の需要の増大によって、鉱山業が発達し、鉱坑は地下深くまで掘られるようになってきました。そのため、深いところから水を汲み上げる必要が生じましたが、約10 m以上の深さになると、ポンプは全く働かなくなりました。井戸掘職人からこの現象を聞いたイタリアの物理学者ガリレオ・ガリレイは、もし「自然が真空を嫌う」なら、水はいくらでも上がるはずであり、アリストテレスの説では、こうした現象を説明できないことに気付いたのです。そこでガリレオは、「自然が真空を嫌う抵抗力」には、限度があるのではないかと考えました。
図.3 ガリレオ・ガリレイは、当時支持されていたアリストテレスの説に疑問を投げかけた
真空の問題は、ガリレオの弟子であった物理学者エヴァンジエリスタ・トリチェリーによって、新たな曲面を迎えました。トリチェリーは、水H2Oの13.6倍の密度を持つ水銀Hgを用いて、その上がり得る高さを推測したのです。一方の端が閉じた長さ約1 mのガラス管に水銀Hgを満たし、そのガラス管をあらかじめ水銀Hgで満たしてある容器に垂直に立てました。実験の結果、ガラス管内の水銀Hgは、約760 mmの高さでピタリと止まり、管の上部に「空所」を生じました。この空所こそ、今まで誰も見たことのない「真空」だと、トリチェリーは考えたのです。さらに、トリチェリーの素晴らしいところは、水銀柱が宙に停止する原因を、初めて大気の重さに求めたところです。トリチェリーはこのことを、次のように表現しています――「我々は、いわば空気の大洋の中に浸って生きている」と。
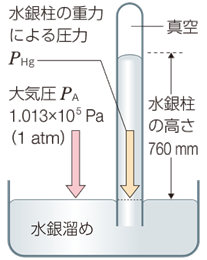
図.4 トリチェリーの実験
トリチェリーの実験は、760 mmの高さの水銀柱の圧力と、大気圧がつり合ったために起こる現象です。ガラス管の中の水銀Hgは外に出ようにも、大気がそれを阻止しようと圧をかけているので、外に出られないのです。このとき、ガラス管内の上部はほぼ真空になるので、これを「トリチェリーの真空(Torricellian vacuum)」ということがあります。大気圧を760 mm相当の水銀柱の重力による圧力とみなして、重力加速度を9.8 m/s2、水銀Hgの密度を13.6 g/cm3、筒の断面積をS cm2とすると、大気圧は次のように求められます。
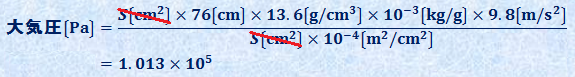
これより、筒の断面積S cm2によらず、760 mmの水銀柱の圧力が、約1.013×105 Paであることが分かります。現在、圧力の単位はSI単位系である「Pa」を使うことが多いですが、慣例として、大気圧を「760 mmHg(ミリメートル水銀柱)」と表すことも多いです。「mmHg」は「Torr(トル)」と書くこともありますが、これはトリチェリーの名にちなんだものです。
1気圧 ＝ 101325 Pa ＝ 760 mmHg ＝ 760 Torr
また、トリチェリーの行った実験では、水銀Hgの代わりに別の液体を使うこともできますが、水銀Hgが最も合理的な液体だと考えられています。この理由は、水銀Hgの密度が大きく、データの測定がしやすいという点と、水銀Hgの蒸気圧が小さいために、蒸気圧を無視できるという点にあります。例えば、水銀Hgの代わりに水H2Oを使った場合は、水H2Oの密度は約1.0 g/cm3なので、水柱の高さは0.76×13.6＝10.336 mにもなります。実際に10 mの筒を用意して、これを実験で行うのは、現実的ではありません。また、水銀Hgの蒸気圧を無視できることは、実験時の温度を考えなくても良い点で、実験が簡単になります。このような利点から、大気圧の測定には、水銀Hgが好まれて使われるのです。
実はトリチェリーと同じ頃、日本にも空気の存在を明らかにした人がいました。「たくあん漬」の考案者であるといわれる沢庵宗彭がその人です。沢庵は、著書「東海夜話」の中で、「空気は目に見えないから存在しないように思うが実際にはあるのだ」と述べ、その証拠として、次のような例をあげています。「子供が遊ぶ竹鉄砲では、噛んで柔らかくした紙玉を竹の筒の前後に入れて、後の玉を突くと、後の玉が前の玉へ届く前に“はしっ”と鳴って、前の玉は飛び出てゆく。これは、その玉の間には空気が満ちているからだ」と。この「竹鉄砲」は、今では小学校4年の「空気でっぽう」という教材で取り上げられ、子どもたちは空気の伸び縮みを学習しています。
(2) 気体法則の歴史
(i) ボイルの法則
大気圧の発見に好奇心をかきたてられたイギリスの物理学者であるロバート・ボイルは、自分でも真空ポンプを作り、それを用いた実験で気体の性質を調べました。そして1662年、気体の圧力と体積について、「同温で一定量の気体の体積はそれに働く圧力に反比例する」という法則を見出しました。この関係を「ボイルの法則(Boyle's law)」といいます。「シリンダーの中に気体を入れて栓をする。気体が漏れないように栓を押していくと、気体の体積は小さくなる。気体はまるでバネのように押せば縮み、離すと元に戻る。同様に、真空の容器の中では空気を入れた子羊の膀胱は膨張し、真空ポンプを停止させると元に戻る」とするのがボイルの法則です。ボイルの法則は、気体の体積をV、圧力をpとすると、次式で表されます。
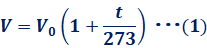
図.5 ボイルの法則
ボイルの法則が成り立つのは、気体の体積と単位体積当たりの気体粒子数が、反比例の関係にあるからです。例えば、気体が入っている容器の内容積を1/2にすると、単位体積当たりの気体粒子数は2倍になります。したがって、器壁への気体粒子の衝突回数も単位時間当たりで2倍になり、気体の示す圧力も2倍となるのです。
なお、ボイルの法則は、十分に圧力が低い領域でしか成り立たない法則です。ボイルの法則では、気体は温度一定で圧力を上げれば、いくらでも体積が小さくなることを示していますが、実際の気体では、ある程度の圧力を超えると凝縮あるいは昇華が起こって、液体や固体になってしまうからです。
(ii) シャルルの法則
気体の圧力が一定のとき、気体の温度が上昇すると、体積はどんどん大きくなっていきます。0℃のときの体積をV0〔L〕、t℃のときの体積をV〔L〕とすると、体積Vは次のように表されます。
この式より、気体はt＝-273℃ではV＝0 Lとなることが分かり、これより低い温度はないことが推定されます。そして、この-273℃を下限の温度とする「絶対温度(absolute temperature)」が新しく使われるようになりました。絶対温度には、単位として「K(ケルビン)」を用います。絶対温度T〔K〕は、セルシウス温度t〔℃〕とは、次のような関係になります。
図.6 絶対温度とセルシウス温度の関係
T ＝ t ＋ 273
ここでT＝t＋273、T0＝273として、(1)式に代入して式を変形すると、次のような「同圧で一定量の気体の体積はその絶対温度に比例する」という関係が導き出せます。この関係は、1787年にフランスの物理学者であったジャック・シャルルが見出したものであり、この法則を「シャルルの法則(Charles's law)」といいます。
シャルルの法則では、温度が1 K下がるにつれ、体積は0℃のときに比べて1/273だけ減少します。つまり、シャルルの法則で-273℃の体積を求めると、気体の体積は0 Lになります。これが、「絶対零度(absolute zero point)」への概念へとつながっていきました。絶対零度は、すべての気体分子の熱運動がなくなった状態であり、熱力学的に考えられる最低温度です。絶対零度は、絶対温度では0 Kで表され、セルシウス温度で表すと-273.15℃です。1 K程度までは、液体ヘリウムHeによる冷却で実現できますが、0 Kに到達することは技術的に難しいです。
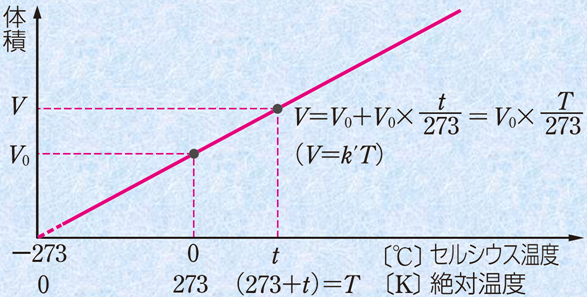
図.7 シャルルの法則
また、実際の気体は温度を下げれば、絶対零度になる前に凝縮あるいは昇華が起こって、液体や固体になります。凝縮が起こる温度は、窒素N2では77 K(-196℃)、ヘリウムHeでは4 K(-269℃)です。液体窒素は、断熱膨張による空気の凝縮で容易に作ることができ、主に冷却材として用いられています。
液体窒素を使った面白い実験があります。液体窒素に手を突っ込むというものです。液体窒素の沸点は-196℃であり、普通に考えれば、突っ込んだ手は大変な凍傷になりそうです。しかし、実際には手を数秒入れただけでは、手に何の傷害も残しません。これは、「ライデンフロスト効果(Leidenfrost effect)」と呼ばれる現象が関係しています。
図.8 液体窒素に手を突っ込んでも凍傷を起こさない
ライデンフロスト効果は、身近なところでも観察することができます。例えば、高温に熱したフライパンに水滴を垂らすと、水滴は瞬時に蒸発することはなく、水滴はフライパンの上をコロコロと転がるように横滑りします。これは、液体がその沸点よりもはるかに高温に熱された固体に触れると、蒸気気体の被膜が液体と固体の間に生じて、液体が固体に直接接することを妨げて、熱伝導を遅らせるためです。そして、実はこれと同じような現象が、液体窒素と手の間にも起こっているのです。液体窒素の沸点(-196℃)に比べると、手の温度(約36℃)ははるかに高温です。液体窒素に手を突っ込んだ瞬間、生じた気体窒素の被膜が皮膚表面に生じて熱伝導を遅らせるため、凍傷には至らないのです。ただし、ライデンフロスト効果は熱伝導を遅らせるだけなので、手を突っ込むのは1〜2秒に留めておいた方がいいと思います。
(iii) アボガドロの法則
1808年、フランスの化学者であるジョセフ・ゲーリュサックは、「各種気体間の反応において、気体の体積の間には簡単な整数比が成り立つ」という「気体反応の法則(law of combining volumes)」を発表しました。しかし、この法則は、当時の化学者にはあまり受け入れられませんでした。これを説明するために、イタリアの化学者であるアメデオ・アボガドロは、「同温同圧のもとで、一定体積中に含まれる気体粒子の物質量は等しい」という関係を見出しました。この関係を「アボガドロの法則(Avogadro's law)」といいます。アボガドロの法則は、気体の体積をV、気体粒子の物質量をnとすると、次のように表されます。
(iv) 理想気体の状態方程式
これより、(i)ボイルの法則・(ii)シャルルの法則・(iii)アボガドロの法則を、1つの法則としてまとめてみましょう。今、(P, V, T, n)で表される点Oと、(P3, V3, T3, n3)で表される点IIIの関係を導いてみます。(i)〜(iii) の諸法則が使えるようにするために、このO→IIを点I (P1, V1, T1, n1)と点II (P2, V2, T2, n2)のステップにさらに分けます。
点O (P, V, T, n) → 点I (P1, V1, T1, n1) → 点II (P2, V2, T2, n2) → 点III (P3, V3, T3, n3)
ただし、O→Iではボイルの法則を用いるためにT＝T1, n＝n1、I→IIではシャルルの法則を用いるためにP1＝P2, n1＝n2、II→IIIではアボガドロの法則を用いるためにP2＝P3, T2＝T3の関係が成り立っているとします。これらをまとめると、次のように表せます。
まず、式(2)と式(3)のそれぞれを体積V1の式に変形して、体積V1を消去すると、式(5)が得られます。そして、T＝T1, P1＝P2の関係があるので、式(5)は式(6)で示されるような「一定量の気体の体積は圧力に反比例し、絶対温度に比例する」という関係の式に変形することができます。この式は、一般的に「ボイル・シャルルの法則(combined gas law)」と呼ばれています。
さらに、式(4)と式(6)のそれぞれを体積V2の式に変形して、体積V2を消去すると、式(7)が得られます。そして、n2＝n, T2＝T3の関係があるので、式(7)は式(8)のように変形することができます。この式は、ボイルの法則・シャルルの法則・アボガドロの法則をまとめ上げた式であり、どのような気体に関しても、
の値が常に一定になることを表しています。
この定数kを定数Rとすると、PV＝nRTという「理想気体の状態方程式(ideal gas law)」が導かれます。理想気体の状態方程式PV＝nRTを利用することで、気体の密度から分子量を決定することができます。例として、質量w gで分子量Mの気体に理想気体の状態方程式PV＝nRTを使ってみましょう。まず、物質量は
のように表すことができるので、理想気体の状態方程式PV＝nRTは、式(9)のように変形することができます。
さらに、気体の密度をd〔g/L〕とすると、
のように表すことができるので、式(9)は式(10)のように変形できます。式(10)を用いることで、気体の分子量を求めることができるのです。
ただし、理想気体の状態方程式PV＝nRTは、1つの気体の情報であることに注意しましょう。圧力Pを変えたり、体積Vを変えたり、温度Tを変えたり、物質量nを変えたり･･････というような状態の変化がある場合には、ボイルの法則・シャルルの法則・アボガドロの法則を使う必要があります。しかし、これらの諸法則も、すべて理想気体の状態方程式PV＝nRTに含まれているのだから、物質量nが一定の場合は、ボイル･シャルルの法則を使えば、どのような問題にも対応できます。
ボイル･シャルルの法則において、左辺に変化前の気体の情報、右辺に変化後の気体の情報を書いて計算すれば、状態の変化がある気体の量(圧力・体積・温度)が分かります。また、気体定数Rは、使用する圧力や体積の単位によって数値が変化します。高校化学では、圧力の単位として〔Pa〕、体積の単位として〔L〕を使うことが多いですが、高校物理では、圧力の単位として〔Pa〕、体積の単位として〔m3〕を使うことが多いです。
|
圧力Pa、体積Lの場合 ・・・R＝8.31×103〔Pa･L/(mol･K)〕 圧力Pa、体積m3の場合・・・R＝8.31〔J/(mol･K)〕 圧力atm、体積Lの場合・・・R＝0.082〔atm･L/(mol･K)〕 |
ちなみに、気体定数Rは次のように求めます。気体の標準状態(273 K, 1.013×105 Pa)におけるモル体積Vm＝22.4 L/molを理想気体の状態方程式PV＝nRTに代入するのです。
また、気体定数Rは、アボガドロ定数NA＝6.02×1023 /molとボルツマン定数k＝1.38×10−23 J/Kの積で求めることもできます。つまり、ボルツマン定数kは、分子１個当たりの気体定数を表す量ということになります。
(3) 混合気体
互いに反応しない2種類以上の気体を1つの容器に充填すると、各気体の成分は拡散の原理により、高濃度の領域から低濃度の領域に移動し、均一な気体となります。このように2種類以上の気体を含んでいる気体を「混合気体(mixed gas)」といいます。また、混合気体中のそれぞれの気体を「成分気体(component gas)」といいます。混合気体を扱うときに必ず問題となるのが、各成分気体がどのような比率で含まれているのかということです。これらの比率を考えるときは、混合気体を分離して、1つの成分気体について、仮想的な状態を設定してやらなくてはなりません。混合気体を分離するとき、その方法には、圧力Pと温度Tを一定にして分離する方法と、体積Vと温度Tを一定にして分離する方法の2種類があります。
(i) 体積と温度が一定のとき
気体Aと気体Bの混合気体について、体積Vと温度Tを一定のまま、圧力を変えて仮想的に分離した状態を考えます。なお、混合気体の圧力を「全圧(total pressure)」といい、各成分気体が単独で混合気体の全体積Vを占めるときの圧力を「分圧(partial pressure)」といいます。混合気体の圧力をP全、気体Aの圧力をPA、気体Bの圧力をPBとすると、次のようになります。
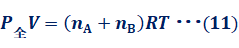
図.9 圧力を変えて混合気体を分離する
式(11), 式(12), 式(13)より、nAとnBを消去すると、次のような式(14)が得られます。
この式(14)を「ドルトンの分圧の法則(Dalton's law)」といいます。混合気体の全圧P全は、各成分気体の分圧PAとPBの和に等しくなるのです。また、分圧PAとPBは、全圧P全とその成分気体のモル分率の積で表されます。これは、分圧の比が各成分気体の物質量の比に等しいことを示しています。また、同温同圧では気体の物質量は体積に比例するので、分圧の比は混合前の各成分気体の体積比にも等しいです。
気体を水上置換で捕集すると、捕集された気体は水蒸気との混合気体になります。したがって、捕集気体の分圧は、捕集気体の全圧から水蒸気の分圧を引いた値です。なお、このときの混合気体の全圧は、大気圧と等しいです。つまり、捕集気体の分圧は、大気圧から水蒸気圧を引いた値と等しくなります。
捕集気体の分圧 ＝ 大気圧 − 水蒸気圧
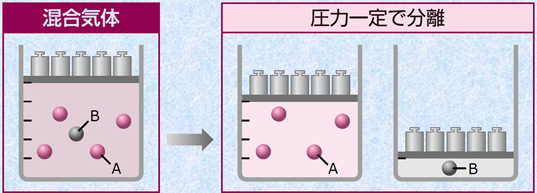
図.10 水上置換では見かけの捕集気体の圧力は水蒸気圧の分だけ大きくなっている
(ii) 圧力と温度が一定のとき
アボガドロの法則によると、一定温度Tと一定圧力Pで、気体の体積Vは気体粒子の数に比例します。この法則は、混合気体でも同じように成り立ちます。まず、気体Aと気体Bの混合気体について、圧力Pと温度Tを一定のまま、体積を変えて仮想的に分離した状態を考えます。なお、混合気体の体積を「全体積(total volume)」といい、各成分気体が単独で混合気体の全圧Pを示すときの体積を「分体積(partial volume)」といいます。混合気体の体積をV全、気体Aの体積をVA、気体Bの体積をVBとすると、次のようになります。
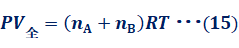
図.11 体積を変えて混合気体を分離する
式(15), 式(16), 式(17)より、nAとnBを消去すると、次のような式(18)が得られます。
混合気体の全体積V全は、各成分気体の分体積VAとVBの和に等しくなるのです。また、分体積VAとVBは、全体積V全とその成分気体のモル分率の積で表されます。これは、分体積の比が、各成分気体の物質量の比に等しいことを示しています。
(iii) 混合気体のまとめ
気体Aと気体Bの混合気体の全圧をP全、全体積をV全、物質量の和をn全としたとき、理想気体の状態方程式より
が成立します。また、各成分気体の分圧をPAとPB、分体積をVAとVBとすると、次の表.1のような関係が成り立ちます。
表.1 分圧と分体積の関係
|
|
分圧の状態方程式 |
分体積の状態方程式 |
|
気体Aの状態方程式 |
|
|
|
気体Bの状態方程式 |
|
|
表.1の関係において、十分に注意しなければならないことは、分圧というのは、飽くまでVとTを一定にして分離したときの成分気体の圧力であり、分体積もまた、PとTを一定にして分離したときの成分気体の体積であることです。よくある間違いとして、分圧の状態方程式を作るときに、体積としてその成分の分体積を使ってしまうことがあるのです。つまり、
や
などの式は、化学的に間違った式ということになります。1つの成分気体が与えられたとき、その成分の物質量nで決めることができるのは、PかVのどちらか一方であることに注意しましょう。
(4) 理想気体と実在気体の違い
気体の本質は、「ほとんどが空間であること」と「ほとんど自由な粒子の運動であること」の2点に集約されます。つまり、完全に空間かつ完全に自由な粒子の運動を持つ気体は、気体としての本質を完璧に備えたものになります。ただし、実在する気体の粒子は、それ自身の体積を持ち、また気体粒子間の分子間力は決して消えはしないのだから、そのような理想的な気体は、観念上でしか存在しません。このように、分子間力が働かず、分子自身の大きさもゼロという理想化された気体を「理想気体(ideal gas)」といいます。これに対して、実在する気体は「実在気体(real gas)」といいます。実在気体では、分子間力が働いており、分子自身の大きさもゼロではありません。
表.2 理想気体と実在気体
|
|
分子自身の大きさ |
分子間力 |
理想気体の状態方程式 |
冷却・圧縮下 |
|
理想気体 |
大きさはゼロ |
分子間力はゼロ |
厳密に成立する |
気体のまま |
|
実在気体 |
大きさがある |
分子間力がある |
厳密には成立しない |
凝縮または凝固する |
理想気体と実在気体とを比較すると、(i)分子自身の大きさの効果と(ii)分子間力の効果により、その振る舞いに差異が見られることになります。
(i) 分子自身の大きさの効果
同温同圧下で、理想気体と実在気体とを比較すると、分子自身の大きさの効果により、実在気体の方が気体の占める体積が大きくなります。しかし、低圧にして全体積を大きくしてやると、分子自身の大きさの効果は相対的に小さくなります。つまり、高圧では分子自身の大きさの効果が顕著になり、低圧では分子自身の大きさの効果は弱まります。
|
分子自身の大きさの効果により、実在気体の方が理想気体よりも体積が大きくなる |
(ii) 分子間力の効果
同温同圧下で、理想気体と実在気体とを比較すると、分子間力の効果により、実在気体の方が気体の占める体積が小さくなります。しかし、低圧にして全体積を大きくしてやると、分子間力の効果は相対的に小さくなります。つまり、高圧では分子間力の効果が顕著になり、低圧では分子間力の効果は弱まります。
|
分子間力の効果により、実在気体の方が理想気体よりも体積が小さくなる |
(iii) 実在気体を理想気体に近付ける
つまり、低圧にすれば、「分子自身の大きさ」と「分子間力」の2つの効果が打ち消しあって消えていくのだから、たいていの気体は低圧にするだけで理想気体に近づきます。さらに、気体を高温にすると、気体粒子の熱運動が激しくなって、粒子間に働く分子間力が、気体の体積や圧に与える影響が相対的に消えていきます。つまり、高温低圧にすれば、実在気体を理想気体に近づけることができます。
また、理想気体と実在気体の違いを論ずるとき、次の図.12のようなグラフを用いることが多いです。このグラフは、様々な圧力下で1 molの気体の体積を測定してPV/(RT)を計算し、圧力Pとの関係を示したものです。理想気体では、n＝1のときPV/(RT)＝1となるから、実在気体1 molのPV /(RT)が1からどの程度ずれるかで、その実在気体がどのような性質を持っているのかが分かるのです。すなわち、PV/(RT)＞1なら理想気体より体積が大きく、PV/(RT)＜1なら理想気体より体積が小さいということが分かります。
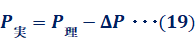
図.12 各種気体1 molのPV/(RT)-P曲線
低圧では、いずれの気体も理想気体に近づくので、PV/(RT)≒1となります。しかし、気体の圧力を上げていくと、理想気体と実在気体とのずれが徐々に大きくなっていきます。圧力を上げても、比較的理想気体に近い振る舞いをする実在気体としては、水素H2やヘリウムHeのような分子量の小さい無極性分子があげられます。これは、分子量が小さいほど、分子自身の大きさや分子間力が小さくなるからです。さらに、無極性分子は極性分子よりも分子間力が小さくなるので、無極性分子の方が理想気体に近くなります。
|
低分子量の無極性分子は、理想気体に近い振る舞いをする（グラフが下に凸にならない） |
一方で、二酸化炭素CO2のように分子量が大きい分子や、塩化水素HClのように極性のある分子では、圧力を上げていくと、理想気体とのずれが顕著になります。このような分子は、低圧力領域ではPV/(RT)＜1（理想気体より体積が小さい）ですが、徐々にPV/(RT)の値が大きくなっていき、高圧力領域ではPV/(RT)＞1（理想気体より体積が大きい）となります。このように曲線がV字型になる理由は、圧力の変化により、分子自身の大きさの効果と分子間力の効果の寄与が変わるからです。
高圧力領域で実在気体がPV/(RT)＞1（理想気体より体積が大きい）となるのは、圧力が大きくなって全体積が小さくなると、空間に占める分子自身の大きさの効果が強くなるからです。したがって、圧力が大きいときは、理想気体より体積が大きくなって、PV/(RT)＞1となるのです。
|
高圧力領域では、分子自身の大きさの効果により、PV/(RT)＞1となる |
また、低圧力領域で実在気体がPV/(RT)＜1（理想気体より体積が小さい）となるのは、分子間力の効果により気体粒子が引き合って、気体の占める空間が小さくなるからです。理想気体では分子間力が働かないので、体積は圧力に完全に反比例します。しかし、実在気体では分子間力が働くために、体積が理想気体より小さくなるのです。したがって、圧力が小さいときは、理想気体より体積が小さくなって、PV/(RT)＜1となります。
|
低圧力領域では、分子間力の効果により、PV/(RT)＜1となる |
(5) ファンデルワールスの実在気体の状態方程式
実在気体は、「分子間力」や「分子自身の体積」を持つため、厳密には「理想気体の状態方程式PV＝nRT」が成立しませんでした。それでは、「分子間力」や「分子自身の体積」を考慮して、実在気体にも適用できる方程式を求めてみましょう。
(i) 圧力の補正
理想気体では、分子間に働く引力がないと仮定しています。しかし、実在気体には、分子間に働く引力があります。容器の内壁に熱運動をして衝突しようとする分子を考えてみましょう。分子は壁との衝突により衝撃力を与え、それを時間的平均値としたものが圧力です。もし壁にぶつかる分子の背後にもう1つの分子があって、それが分子間力を及ぼしていれば、衝撃力は弱まります。すなわち、実在気体では、分子間力が存在するため、理想気体に比べると、容器内の壁に衝突するときの圧力が低下します。このことを考えて、圧力を補正してみましょう。圧力の低下分をΔPとすると、実在気体の圧力P実と理想気体の圧力P理は、次のような関係で表せます。
圧力の低下分ΔPは、「2分子が出会う確率」と「分子間力の強さ」に比例すると考えます。ここで、「3分子以上が出会う確率」は、確率が低過ぎるので無視できます。特定の場所に分子がいる確率は、単位体積当たりの分子数
に比例するので、2分子が出会う確率は
に比例します。分子間力の強さも含めて比例定数をαとすると、ΔPは次のように表せます。
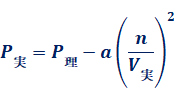
そこで、式(19)は次のように表せます。
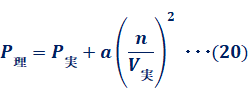
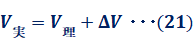
(ii) 体積の補正
理想気体では、分子自身の体積を0と仮定しています。しかし、実在気体では、分子自身の体積分だけ、理想気体より体積が大きくなります。そこで、増加分をΔVとすると、実在気体の体積V実と理想気体の体積V理は、次のような関係で表せます。
気体1 mol当たりの体積増加分をbとすると、物質量がnの場合は、ΔV＝nbと表せます。よって、式(21)は次のように表せます。なお、bは分子自身の体積に比例した、気体の種類によって異なる定数です。
(iii) 実在気体の状態方程式
式(20)と式(22)より、理想気体の状態方程式PV＝nRTに代入すると、次のような方程式が得られます。これは、「ファンデルワールスの実在気体の状態方程式(Van der Waals real gas state equation)」と呼ばれています。この式で、定数αは分子間に働く引力を反映し、定数bは分子自身の体積を反映しており、これらはともにファンデルワールス定数と呼ばれます。αとbは、気体の種類によって異なる値を取ります。
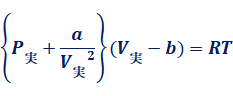
特に1 molの気体については
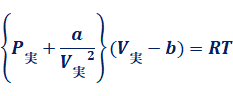
・参考文献
1) 石川正明「新理系の化学(上)」駿台文庫(2005年発行)
2) 井沢省吾「自動車誕生に貢献した化学の歴史と今後」化学と教育69巻9号(2021年)
3) 齊藤烈/藤嶋昭/山本隆一/他19名「化学」啓林館(2012年発行)