・溶液化学(希薄溶液の束一性)
【目次】
(1) 希薄溶液の束一性とは何か?
希薄溶液における「束一性(colligative properties)」とは、不揮発性溶質を含む希薄溶液の状態変化などに関する性質のことで、物質の種類あるいは性質によらず、濃度だけによって決定される性質をいいます。希薄溶液の束一性は、「存在する溶質粒子の数だけに依存する」という特性があるのです。状態変化とは、固体・液体・気体間の物理変化のことですが、希薄溶液のように純溶媒に不純物が少量混在している場合、純溶媒の状態変化が不純物に阻害され、純溶媒の沸点や凝固点が変化してしまいます。
後に説明する蒸気圧降下・沸点上昇・凝固点降下・浸透圧などの現象は、同一溶媒であれば、溶質の種類によらず、質量モル濃度(浸透圧の場合はモル濃度)だけで決まります。言い換えれば、希薄溶液の束一性は、溶質粒子の濃度だけで決まるのです。粒子の種類は問わないのだから、溶質粒子が電解質の場合には、電離後の全溶質粒子の濃度を考えなければなりません。この場合、見かけの溶質の濃度は大きくなります。また、溶質粒子が水素結合などで会合する場合には、見かけの溶質の濃度は逆に小さくなります。
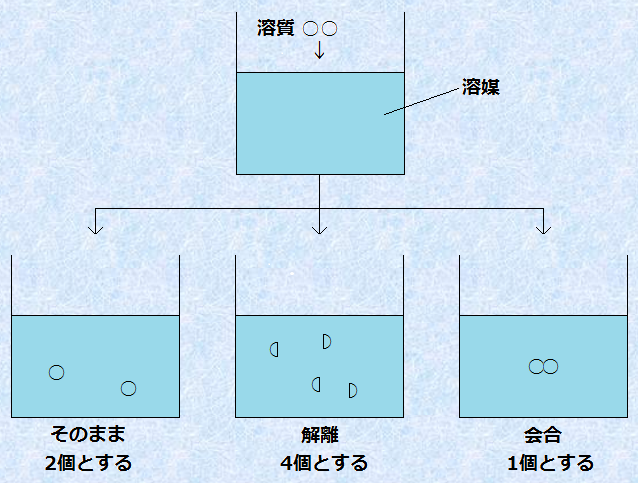
図1. 溶媒中の粒子の数え方
なお、希薄溶液において、溶質粒子の種類による影響が現れないのは、希薄溶液では溶質粒子が互いに十分に離れている状態であり、その溶質粒子の個性が全く表に出てこないからです。 一方で、濃厚溶液では、溶質粒子同士が接近する機会が多くなり、溶質粒子間の相互作用の影響が現れてきます。よって、溶液は溶質粒子の種類によって、それぞれ異なる性質を示すようになり、その扱いは一層難しくなります。
(2) 蒸気圧降下
純水と砂糖水(スクロースC12H22O11水溶液)を同条件で放置すると、純水の方が砂糖水よりも早く蒸発していきます。砂糖水などの水溶液では、純水に比べて、水の蒸発が起こりにくくなっているのです。そのため、水溶液では、気液平衡に達したときに水蒸気の示す圧力(蒸気圧)が、純水に比べて小さくなります。一般的に不揮発性の物質を溶かした溶液の蒸気圧は、純溶媒が示す蒸気圧よりも小さくなり、この現象は「蒸気圧降下(vapor pressure depression)」と呼ばれています。
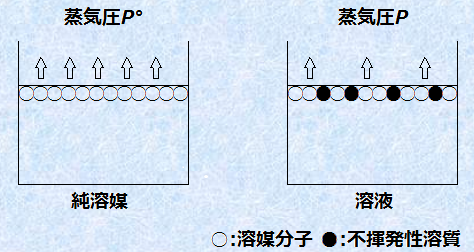
図.2 蒸気圧降下のモデル
溶液中に不揮発性溶質が存在していると、液体-気体界面に存在する不揮発性溶質の分だけ、他の相へ移動する溶媒粒子の接近が阻害され、溶液の蒸気圧が減少します。したがって、不揮発性溶質が存在している溶液の蒸気圧は、純溶媒の示す蒸気圧よりも小さくなります。一般的に希薄溶液では、次のような関係が成り立つのです。
純溶媒の蒸気圧P。 > 溶液の蒸気圧P
さらに、希薄溶液では、各成分が互いに異なる分子間力を及ぼし合わず、また各成分が均一に混ざり合っていると仮定できます。この仮定に基づくと、「溶液の蒸気圧は溶液中のモル分率と純溶媒の蒸気圧の積で表される」という、「ラウールの法則(Raoult's law)」が成り立ちます。また、このようにラウールの法則が成り立つ溶液を、一般的に「理想溶液(ideal solution)」といいます。
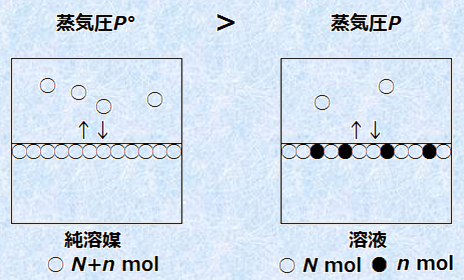
図3 ラウールの法則の例
![]()
![]()
このときの蒸気圧降下度をΔPとします。P。>Pより、ΔP=P。−Pと表せるので、蒸気圧降下度ΔPは、次のように表せます。
![]()
![]()
![]()
希薄溶液では、N >>nの関係が成立しているので、N+n≒Nの近似ができ、蒸気圧降下度ΔPは、次のように表せます。
![]()
ここで、溶媒のモル質量をM溶媒とし、分母と分子にM溶媒×10-3 をかけます。すると、![]() は溶液の質量モル濃度mとなります。分子のM溶媒×10-3×P。 を定数Kとおくと、蒸気圧降下度ΔPは、次のように表せます。
は溶液の質量モル濃度mとなります。分子のM溶媒×10-3×P。 を定数Kとおくと、蒸気圧降下度ΔPは、次のように表せます。
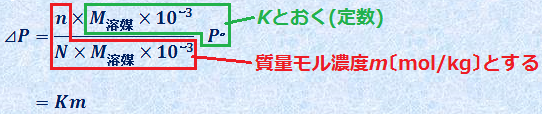
これより、蒸気圧降下度はΔP=Kmとなり、蒸気圧降下度ΔPが溶液の質量モル濃度mに比例するという簡潔な関係になります。ただし、ここでいう「質量モル濃度」は、全溶質粒子の質量モル濃度であることに注意してください。すなわち、溶質粒子の解離や会合が起こる場合は、計算上の質量モル濃度が変化します。
(3) 沸点上昇
不揮発性の物質を溶かした溶液では、蒸気圧降下が起こるため、蒸気圧が小さくなります。そのため、温度を上げていったときに、蒸気圧が大気圧と等しくなる温度が高くなります。蒸気圧が大気圧と等しくなると、液体では沸騰が起こります。このときには、液体の表面だけでなく、内部からも気化が起こるようになります。つまり、不揮発性の物質を溶かした溶液では、沸点が高くなるのです。この現象を「沸点上昇(rise of boiling point)」といい、希薄溶液では、一般的に次式が成り立ちます。なお、沸点上昇度ΔTbは、溶質のモル濃度mではなく、全溶質粒子のモル濃度Σmに比例することに注意が必要です。すなわち、溶質粒子の解離や会合が起こる場合は、計算上の質量モル濃度が変化します。
|
ΔTb=Tb−Tb。=KbΣm ΔTb:沸点上昇度〔K〕、Tb:溶液の沸点〔K〕、Tb。:純溶媒の沸点〔K〕 Kb:モル沸点上昇〔K・kg/mol〕、Σm:全溶質粒子の質量モル濃度〔mol/kg〕 |
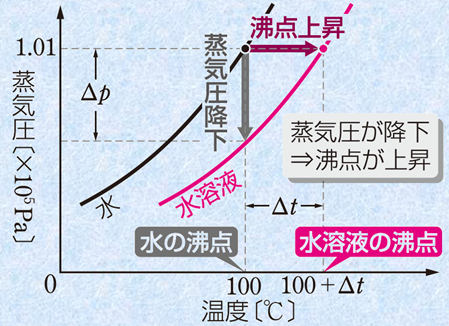
図.4 蒸気圧降下と沸点上昇
(4) 凝固点降下
純水は0℃で凝固しますが、海水は-1.86℃以下にならないと凝固しません。1 Lの海水中には、約29 gもの塩化ナトリウムNaClが溶けているからです。さらに、凍った海水の周りで塩分濃度が高まり、濃度25%の飽和食塩水になると、-22℃まで凍らなくなります。溶液を冷却したとき、溶質粒子の存在のために、溶媒の凝固は妨げられます。そのため、溶液の凝固点は、純溶媒の凝固点よりも低くなります。すなわち、0℃では、溶解する水分子の数>凝固する水分子の数であるから、溶液を固液平衡の状態にするには、さらに低温にして、凝固する水分子の数を増やしてやらなければならないのです。このように、溶液の凝固点は純溶媒よりも低くなり、この現象を「凝固点降下(depression of freezing point)」といいます。希薄溶液では、一般的に次式が成り立ちます。なお、凝固点降下度ΔTfは、溶質のモル濃度mではなく、全溶質粒子のモル濃度Σmに比例することに注意が必要です。
|
ΔTf=Tf−Tf。=KfΣm ΔTf:凝固点降下度〔K〕、Tf:溶液の凝固点〔K〕、Tf。:純溶媒の凝固点〔K〕 Kf:モル凝固点降下〔K・kg/mol〕、Σm:全溶質粒子の質量モル濃度〔mol/kg〕 |
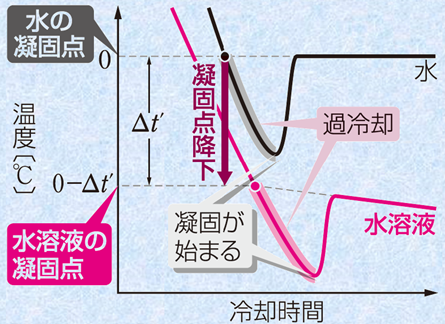
図.5 凝固点降下
溶液が凝固するときに、実際に固体となるのは、溶媒粒子だけです。したがって、冷却を続けて、氷などの固体ができる場合、溶液の濃度は、どんどん大きくなっていきます。そうなると、凝固点降下ΔTf=Kf Σmの式を作るときに、一体どの時点の濃度を使えばいいのか、迷ってしまうかもしれません。しかし、この式は、固相と液相が平衡状態のときにしか成立しないことに注意してください。つまり、氷などの固体が凝固している場合を考えるときは、凝固が完全に終わって、固液平衡になったときの濃度を使えばいいのです。例えば、500 gの水に0.01 molの塩化ナトリウムNaClを溶かし、-0.50℃まで冷却した場合を考えます。このときにできる氷をX gとすると、水のモル凝固点降下Kfは1.85 K・kg/molなので、次のように計算できます。
![]()
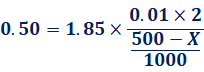
![]()
これより、-0.50℃まで冷却した場合には、氷は426 gできることが分かります。氷などの固体ができる場合は、固体を溶液の系から除いた状態の式を作ればいいのです。また、全溶質粒子の質量モル濃度Σmは、単純に加えた固体の物質量と対応するわけではないことに注意してください。塩化ナトリウムNaClを加えた場合では、水中でナトリウムイオンNa+ と塩化物イオンCl- に電離するので、実際の粒子数は2倍になるのです。
NaCl → Na+ + Cl−
凝固点が低くなって凍りにくくなるということは、溶けやすいということでもあります。雪国ではお馴染みの風景ですが、真冬で気温が氷点下になると、橋の上などに「凍結防止剤」を散布することがあります。橋が零下の寒気にさらされて凍り付くと、滑りやすくなって大変危険です。そのために凍結防止剤を散布して、アスファルトの路面を確保し、道路交通の障害を少なくします。この凍結防止剤には、塩化カルシウムCaCl2や塩化マグネシウムMgCl2などが用いられています。凍結防止剤は、海水と同様に凝固点降下を起こすので、凍る前に道路に散布することが重要です。路上の水に塩化カルシウムCaCl2を散布しておくと、その水溶液は、気温が氷点下なっても凝固しなくなります。路上の水に32%の塩化カルシウムCaCl2を溶かしておくと、理論的には-51℃まで凍らずにしておくことができます。ただし、塩化カルシウムCaCl2は植物を枯らす要因や、皮膚炎の原因になることがあるので注意も必要です。

図.6 豪雪地帯では、冬場に定期的に凍結防止剤の散布を行っている
(5) 状態図における変化
不揮発性の物質を溶かした溶液では、蒸気圧降下・沸点上昇・凝固点降下といった現象が見られました。このような現象が見られる理由は、純溶媒の状態変化が、不揮発性溶質によって阻害され、状態変化における相平衡が変化してしまうからです。これを熱力学の側面から見れば、「溶液に不揮発性の物質を溶かすことによって系の乱雑さが大きくなり、液体の状態が安定になるから」ということもできます。例えば、砂糖の濃厚水溶液に純水を加えてかき混ぜると、砂糖の希薄溶液ができますが、得られた希薄溶液をいくらかき混ぜても、元の濃厚水溶液には戻りません。つまり、溶液中では、溶質粒子と溶媒粒子が無秩序に混じり合っているために、純溶媒中の溶媒分子よりも乱雑さが大きくなり、溶液は熱力学的に安定化しているといえます。沸点上昇や凝固点降下といった現象も、このような溶液の安定性によって説明できます。
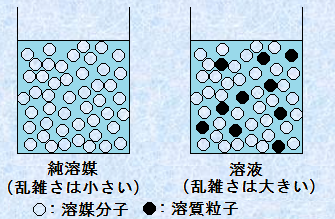
図.7 溶液は純溶媒よりも熱力学的に安定である
まず、水が水蒸気になる場合を考えてみましょう。同じ温度で、純水中の水分子と水溶液中の水分子を比較したとき、溶液中の水分子は熱力学的に安定化されている分だけ、純水中の水分子よりも蒸発しにくいです。これが水溶液の蒸気圧降下であり、その分だけ溶液の沸点は上昇します。次に、水が氷になる場合を考えてみましょう。0℃では、純水中の水分子と氷の水分子は、ほぼ同じ安定性を持っています。しかし、これが水溶液になると、溶質粒子の影響があるので、氷の水分子よりも水溶液中の水分子の方が安定になります。そのため、水溶液中の水分子は、あえて不安定な氷にはなりにくいのです。したがって、水溶液の水分子を氷にするには、もっと低い温度が必要となり、その結果として、水溶液の凝固点は降下します。つまり、液体状態にある物質に不揮発性の溶質を加えると、状態図における液体状態でいる領域が広くなるのです。次の図.8に、溶液の状態図における変化を示します。図.8中で、ΔTfは凝固点降下度、ΔTbは沸点上昇度、ΔPは蒸気圧降下度を表します。
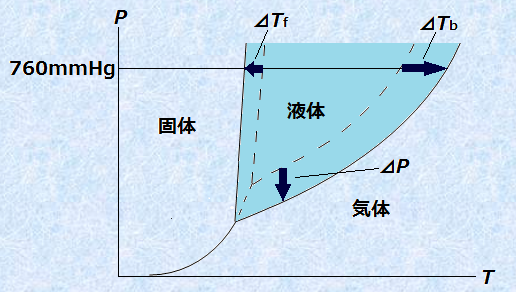
図.8 溶液の状態図における変化
このような溶液の状態図における変化を、日常生活で有効に活用しているものが「寒剤(cryogen)」です。寒剤は、低温状態を得るために用いる冷却剤のことです。アイスキャンディーを氷と食塩の混合物で冷却して作る実験は、小学生向けの化学実験として非常に有名です。試験管にジュースと割りばしを入れ、試験管の周りに氷を敷き詰め、食塩を氷に振りかけます。すると、寒剤による冷却作用でジュースが凍って、アイスキャンディーが作れるのです。他にも、寒剤は漁師が獲った魚を痛まないように、冷却するときなどにも使われます。
ところで、氷に食塩をかけると、なぜ温度が下がるのでしょうか?まず、固相と液相が平衡状態にある氷に食塩NaClをかけると、液相が塩化ナトリウムNaCl水溶液となり、凝固点降下によって、0℃でも水が凝固しなくなります。つまり、氷に食塩NaClをかけると、氷の融解がどんどんと進むことになるのです。ここで、状態変化における融解熱が、吸熱反応であったことを思い出してください。物質は固体から液体に変化するとき、結晶状態にある分子をバラバラにするのにエネルギーが必要となるため、周囲から熱を奪うのです。
H2O(固) = H2O(液) − 6.01 kJ
つまり、氷に食塩NaClをかけると、凝固点降下によって固体の融解が進み、その融解熱によって周囲が冷却されるのです。さらに、実際の冷却では、融解熱の他に食塩NaClの溶解熱による寄与も考えられます。しかし、この寄与は非常に小さいため、通常は無視しても問題ないでしょう。
NaCl(固) + aq = Na+ aq + Cl−aq − 4.2 kJ
また、氷と食塩の組み合わせによる寒剤の実験をすると、「食塩でなくて砂糖ではダメなのか?」という質問がよくされます。結論から言えば、砂糖C12H22O11でも、食塩NaClと同じように冷却することができます。ただし、冷却効率の面から見れば、断然食塩NaClの方が優れています。この理由は、それぞれの溶液の凝固点降下度を計算すれば、すぐに分かります。例えば、10 gの食塩NaCl(M=58.5)と10 gの砂糖C12H22O11(M=342)のそれぞれを500 gの水に溶かしたとして、溶液の凝固点降下度を計算してみましょう。水のモル凝固点降下Kfを1.85 K・kg/molとすると、次のようになります。
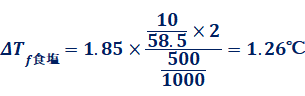
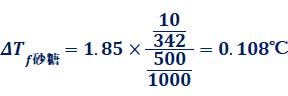
よって、食塩NaClの方が、砂糖C12H22O11よりも凝固点降下度が10倍以上も大きいということが分かります。このように同じ10 gの溶質でも、凝固点降下度で10倍以上の差が現れるのは、砂糖C12H22O11の分子量(M=342)が、食塩NaClの式量(M=58.5)よりもはるかに大きく、また砂糖C12H22O11は非電解質で、食塩NaClは電解質であることが考えられます。食塩NaClは、水に溶かすとナトリウムイオンNa+ と塩化物イオンCl- に電離するため、粒子数が2倍となり、凝固点降下度が大きくなるのです。したがって、凝固点降下度が大きいほど、融解が速やかに進んで、冷却効率が優れることになるので、砂糖C12H22O11よりも食塩NaClを溶かした方がいいのです。
(6) 浸透圧
濃度の異なる2つの溶液を混合して放置すると、溶質粒子は全体に拡散して、均一な濃度の溶液となります。ここで、溶液中の小さな溶媒粒子は自由に通すけれども、大きな溶質粒子は通さないという性質を持つ「半透膜(semipermeable)」で、溶液と純溶媒を仕切っておくと、溶媒粒子が半透膜を通って、溶液の方へ移動していきます。これは、純溶媒中の溶媒分子の方が、溶液中の溶媒分子よりも溶媒自身の濃度が大きく、拡散の原理に従って、溶媒分子が濃度の大きい方から小さい方へと移動するからです。このような現象を「浸透(permeation)」といいます。何だかややこしいようですが、浸透とは、「溶質粒子が溶媒分子を引き込む現象」のことだと思えばいいのです。例えば、次の図.9のように半透膜のチューブの中に着色した砂糖水を入れておくと、浸透現象により水分子が砂糖水の方に移動し、半透膜のチューブが膨らみます。

図.9 半透膜のチューブを用いた浸透実験
なお、実際には半透膜の種類によって、半透膜を通過できる粒子の種類が異なります。例えば、半透膜として汎用されるセロハン膜には、直径3〜4 nmの細孔があって、約0.14 nmの水分子はよく通しますが、デンプンのような巨大分子は通さないので、デンプン水溶液に対しては半透膜の振る舞いをします。しかし、セロハン膜はナトリウムイオンNa+ や塩化物イオンCl− は通過させるので、塩化ナトリウムNaCl水溶液に対しては半透膜といえなくなります。ここでは、「溶液中の溶媒粒子は自由に通すけれども、溶質粒子は通さない」という理想的な半透膜を考えましょう。
半透膜を通って浸透してくる溶媒粒子を阻止するために、溶液側から加える圧力の最小値を「浸透圧(osmotic pressure)」といいます。なお、希薄溶液における浸透圧πは、次の「ファントホッフの式(van's Hoff formula)」で表されます。この式は、オランダの化学者であるヤコブス・ファントホッフが1886年に発表したものであり、この業績によって、ファントホッフは1901年に第1回のノーベル化学賞を受賞しています。
![]()
ここで、Cは全溶質粒子のモル濃度〔mol/L〕、Rは気体定数〔Pa・L/(K・mol)〕、Tは絶対温度〔K〕です。モル濃度Cは、体積Vと物質量nを使うと、C=n/Vと表せます。これより、ファントホッフの式をπV=nRTと変形すると、理想気体の状態方程式PV=nRTと同じ形になることが分かります。ファントホッフは、「溶媒が溶質粒子に何の影響も与えずに体積を保持するためだけにあるとすれば、溶質粒子は水溶液中で気体の分子と同じ挙動を示すはずだ」と考えたのです。しかし、ファントホッフの式πV=nRTは、希薄溶液についてのみ近似的に当てはまり、少し濃い溶液での実験値との不一致は著しいです。浸透圧πは、実験的には次の図.10のようにして求められます。
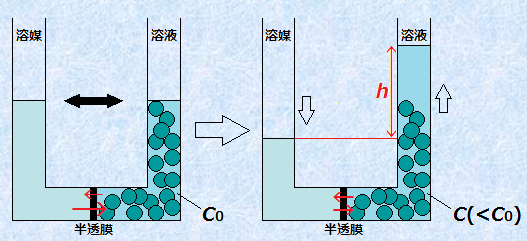
図.10 U字管の場合の浸透圧π
平衡状態になって溶媒の移動が見かけ上なくなり、液面差hになったときにこの状態を保つための圧力が、濃度Cの溶液の浸透圧πに相当します。なお、このときの濃度Cは、浸透してきた溶媒により薄まっているので、初濃度C0とは異なることに注意しなければなりません。つまり、浸透が起こっている間は、浸透圧は刻々と変化しており、浸透後の浸透圧CRTは、浸透前の浸透圧C0RTよりも小さくなります(CRT<C0RT)。
このように、浸透圧には浸透前と浸透後の2種類の値があるので、どの時点の浸透圧を求めたいのか、よく注意する必要があります。例えば、浸透による液面の移動を起こさないように、溶媒と溶液の液面を同じ高さに保つためには、浸透が起こる前に溶液側に圧力を加えなければなりません。このときの圧力(浸透前の浸透圧)は、液面差が0のときなので浸透圧C0RTと等しく、液面差がhのときのCRTではありません。浸透圧がCRTとなるのは、液面差がhとなったときです。なお、浸透後に生じた液面差hを使って、浸透後の浸透圧πを求める方法には、次の2通りがあります。
(i) 液面差hを水銀柱の高さに換算して求める
浸透圧の問題では、水銀Hgの密度13.6 g/cm3が与えられている場合がほとんどです。水銀柱の高さが76 cmのとき、圧力が1.013×105 Paとなるので、液面の高さhを水銀柱の高さに変換することで、浸透圧πを求めることができるのです。ここで、U字管の管径をS cm2、水銀に換算したときの液面差をH cm、溶液の密度をd g/cm3とすると、次のようになります。
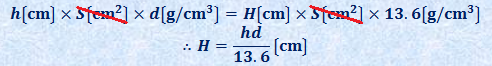
よって、溶液を水銀柱に換算したときの液面差は、H=hd/13.6になります。また、1気圧は1.013×105 Pa=76 cmHgなので、浸透圧πは、1気圧のH /76倍に相当することが分かります。これより浸透圧πを求めると、次のようになります。
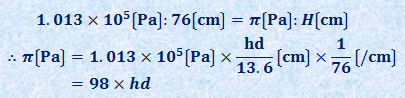
(ii) 液面差hの液柱の重力の及ぼす圧力を求める
液面差hの液柱の重力のおよぼす圧力は、その溶液の浸透圧πに等しいです。U字管の管径をS cm2、溶液の密度をd g/cm3、重力加速度を9.8 m/s2とすると、浸透圧πは次のようになります。
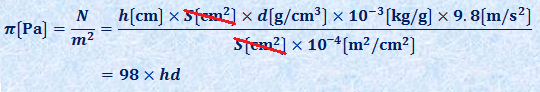
これより、浸透圧πはいずれの方法で求めても、π=98hdという簡潔な関係になります。(ii)の方法では、計算が(i)より簡単になる場合が多いので、浸透圧πを求めるときは、(ii)の方法がお勧めです。ただし、重力加速度g=9.8 m/s2は、化学の問題では与えられていないことが多いので、自分で定義して使うようにしましょう。また、ファントホッフの式π=CRTより、CRT=98hdという関係が成立します。溶質の分子量をM、溶質の質量をw〔g〕、平衡状態における溶液の体積をV〔L〕とすると、次のようになります。
![]()
![]()
![]()
つまり、浸透圧の現象を利用して、未知の物質の分子量Mを調べることができるのです。ただし、この式は溶質の電離や会合を考えていないので、溶質の電離や会合がある場合は、それを考慮した式に変形する必要があります。また、この式において、分子量Mが大きいと液面差hが小さくなり、実験データの測定がしやすくなります。つまり、浸透圧の現象を利用して分子量Mを求める方法は、分子量Mの大きい高分子化合物などの分子量測定に適しているのです。
逆に分子量Mの小さい物質の場合は、凝固点降下ΔTf=KfΣmや沸点上昇ΔTb=KbΣmを利用するといいでしょう。凝固点降下や沸点上昇を利用して分子量Mを調べる方法は、分子量Mが小さいとΔTが大きくなり、実験データの測定がしやすくなります。特にショウノウC10H16Oのモル凝固点降下の値は40.0 K・Kg/molと水H2Oの値1.85 K・Kg/molと比べるとかなり大きく、比較的誤差の少ない分子量測定法として、長らく用いられてきた歴史があります。次に「凝固点降下法(freezing point method)」の式を示します。溶媒の質量をw1、溶質の質量をw2、溶質の添加による凝固点降下度をΔTf、モル凝固点降下をKfとすると、溶質の分子量Mは次のように表せます。
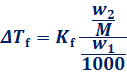
![]()
・参考文献
1) 石川正明「新理系の化学(上)」駿台文庫(2005年発行)
2) 卜部吉庸「化学の新研究」三省堂(2013年発行)
3) 齊藤烈/藤嶋昭/山本隆一/他19名「化学」啓林館(2012年発行)
4) 吉村忠与志「知るほどハマル!化学の不思議」技術評論社(2007年発行)