پE”M‰»ٹw
پy–عژںپz
(2) ƒGƒ“ƒ^ƒ‹ƒsپ[‚ئƒGƒ“ƒgƒچƒsپ[
(4) —^‚¦‚ç‚ꂽ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p•û–@
(1) ‰·“x‚ئ”M—ت
•¨ژ؟‚ج‰·‚©‚³‚â—₽‚³‚حپAپu‰·“x(temperature)پv‚ئ‚¢‚¤ژع“x‚إ•\‚³‚ê‚ـ‚·پB‰·“x‚ھˆظ‚ب‚é2‚آ‚ج•¨ژ؟‚ھگعگG‚·‚é‚ئ‚«پAچ‚‰·‚ج•¨ژ؟‚©‚ç’ل‰·‚ج•¨ژ؟‚ضˆع“®‚·‚éƒGƒlƒ‹ƒMپ[‚ًپu”M(heat)پv‚ئ‚¢‚¢پA‚»‚ج—ت‚ًپu”M—ت(heat capacity)پv‚ئ‚¢‚¢‚ـ‚·پB‚»‚µ‚ؤپAچ‚‰·‚ج•¨ژ؟‚ھژ¸‚ء‚½”M—ت‚ئ’ل‰·‚ج•¨ژ؟‚ھ“¾‚½”M—ت‚حپAڈي‚ة“™‚µ‚‚ب‚è‚ـ‚·پB
•¨ژ؟1 g‚ج‰·“x‚ً1 Kڈم‚°‚é‚ج‚ة•K—v‚ب”M—ت‚ًپu”ن”M(specific heat)پv‚ئ‚¢‚¢پA’Pˆت‚حپuJ/(g¥K)پv‚إ•\‚µ‚ـ‚·پB”ن”M‚ج’l‚حپA•¨ژ؟‚ة‚و‚ء‚ؤˆظ‚ب‚èپAگ…‚ج”ن”M‚ح4.18 J/(g¥K)‚إ‚·پB—ل‚¦‚خپA”ن”McپkJ/(g¥K)پl‚إپAژ؟—تmپkgپl‚ج•¨ژ؟‚ج‰·“x‚ھƒ¢TپkKپlڈمڈ¸‚µ‚½‚ئ‚«پA‚»‚ج•¨ژ؟‚ھ‹zژû‚µ‚½”M—تQپkJپl‚حپAژںژ®‚إ•\‚³‚ê‚ـ‚·پB
![]()
“¯‚¶ژ؟—تmپkgپl‚ج2‚آ‚ج•¨ژ؟‚ھپA‚»‚ꂼ‚ꓯ‚¶”M—تQپkJپl‚ً‹zژû‚ـ‚½‚ح•ْڈo‚µ‚½‚ئ‚«پA”ن”McپkJ/(g¥K)پl‚ھ‘ه‚«‚¢•¨ژ؟‚ظ‚اپA‰·“x•د‰»ƒ¢TپkKپl‚حڈ¬‚³‚‚ب‚è‚ـ‚·پB‚·‚ب‚ي‚؟پA”ن”M‚ھ‘ه‚«‚¢•¨ژ؟‚ظ‚اپA‰·‚ـ‚è‚ة‚‚پA—â‚ك‚ة‚‚‚ب‚è‚ـ‚·پBژں‚ج•\.1‚ةپA—lپX‚ب•¨ژ؟‚ج”ن”M‚ًژ¦‚µ‚ـ‚·پB•\.1‚©‚ç‚حپAگ…H2O‚ج”ن”M‚ھپA”ٌڈي‚ة‘ه‚«‚¢‚±‚ئ‚ھ•ھ‚©‚è‚ـ‚·پBƒqƒg‚جگg‘ج‚ح60%ˆبڈم‚ھگ…H2O‚إ‚إ‚«‚ؤ‚¢‚ـ‚·‚ھپAگ…H2O‚ج”ن”M‚ھ‘ه‚«‚¢‚½‚ك‚ةپAٹO•”‚ج‹C‰·‚ھ•د‰»‚µ‚ؤ‚àپA‘ج‰·‚ً‚ ‚é’ِ“xˆê’è‚ة•غ‚آ‚±‚ئ‚ھ‚إ‚«‚é‚ج‚إ‚·پB
•\.1 —lپX‚ب•¨ژ؟‚ج”ن”M(25پژ)
|
•¨ژ؟ |
”ن”MپkJ/(g¥K)پl |
ƒ‚ƒ‹”ن”MپkJ/(mol¥K)پl |
|
گ… |
4.18 |
75 |
|
•X |
1.94 |
35 |
|
ƒAƒ‹ƒ~ƒjƒEƒ€ |
0.90 |
24 |
|
“S |
0.45 |
25 |
|
“؛ |
0.38 |
24 |
|
‹â |
0.24 |
25 |
(i) Œn‚ئٹOٹE
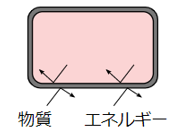
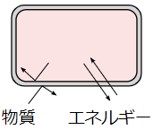
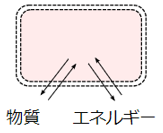
پ@‰»ٹw”½‰‚ھ‹N‚±‚èپAٹدژ@‚ج‘خڈغ‚ئ‚ب‚é•”•ھ‚ًپuŒn(system)پv‚ئ‚¢‚¢پA‚»‚êˆبٹO‚ج•”•ھ‚ًپuٹOٹE(surroundings)پv‚ئ‚¢‚¢‚ـ‚·پBŒn‚ئٹOٹE‚ئ‚جٹش‚إ‚ج‚â‚èژو‚è‚ھ‰آ”\‚ب‚à‚ج‚ح•¨ژ؟(—±ژq)‚ـ‚½‚حƒGƒlƒ‹ƒMپ[‚ج‚ف‚إپA‰»ٹw”½‰‚إ‚حŒn‚ئٹOٹE‚ئ‚جٹش‚إ”M‚جڈo“ü‚è‚ً”؛‚¤‚±‚ئ‚ھ‘½‚¢‚إ‚·پBŒn‚ة‚ح—lپX‚ب–¼ڈج‚ھ‚ ‚èپAپuŒا—§Œnپvپu•آچ½ŒnپvپuٹJ•ْŒnپv‚ب‚ا‚ھ‚ ‚è‚ـ‚·پBˆê”ت“I‚ب‰»ٹw”½‰‚حپuٹJ•ْŒnپv‚إ‹N‚±‚邱‚ئ‚ھ‘½‚پAپuٹJ•ْŒnپv‚إ‚ح•¨ژ؟‚ئƒGƒlƒ‹ƒMپ[‚ج—¼•û‚ج‚â‚èژو‚è‚ھ‰آ”\‚إ‚·پBژں‚ج•\.2‚ة—lپX‚بŒn‚جژي—ق‚ًژ¦‚µ‚ـ‚·پB
•\.2 —lپX‚بŒn‚جژي—ق
|
–¼ڈج |
Œا—§Œn |
•آچ½Œn |
ٹJ•ْŒn |
|
•¨ژ؟‚ج‚â‚èژو‚è |
پ~ |
پ~ |
پ› |
|
ƒGƒlƒ‹ƒMپ[‚ج‚â‚èژو‚è |
پ~ |
پ› |
پ› |
|
گ} |
|
|
|
‰»ٹw”½‰‚ً—ک—p‚µ‚ؤپA”M‚ً“¾‚é‚à‚ج‚جˆê‚آ‚ةƒJƒCƒچ‚ھ‚ ‚è‚ـ‚·پBƒJƒCƒچ‚ج’†‚ة‚ح“S•²Fe‚ھ“ü‚ء‚ؤ‚¨‚èپA‚±‚ê‚ھ‹َ‹C’†‚جژ_‘fO2‚ئ”½‰‚µ‚ؤپAƒIƒLƒVگ…ژ_‰»“S(III) FeO(OH)‚ب‚ا‚ھگ¶گ¬‚µ‚ـ‚·پB‚±‚ج‚ئ‚«پA“SFe 1mol“–‚½‚è419 kJ‚ج”M—ت‚ھŒn‚©‚ç•ْڈo‚³‚êپAٹOٹE‚ة‚¢‚éژ„‚½‚؟‚ح”M‚ًژَ‚¯ژو‚ء‚ؤ‰·‚ـ‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB‚±‚ج‚و‚¤‚ةپAŒn‚ج”M‚ًٹOٹE‚ة•ْڈo‚µ‚ب‚ھ‚çگi‚ق”½‰‚ًپu””M”½‰(exothermic reaction)پv‚ئ‚¢‚¢‚ـ‚·پB
4Feپ@پ{پ@2H2Oپ@پ{پ@3O2پ@پ¨پ@4FeO(OH)
پ@‚ـ‚½پA—â‹pچق‚ج’†‚ة‚حپAڈةژ_ƒJƒٹƒEƒ€KNO3‚ئگ…‚ھ“ü‚ء‚ؤ‚¢‚é‚à‚ج‚ھ‚ ‚è‚ـ‚·پBڈةژ_ƒJƒٹƒEƒ€KNO3‚ھگ…‚ة—n‚¯‚éچغ‚ةڈةژ_ƒJƒٹƒEƒ€KNO3 1 mol“–‚½‚è35 kJ‚ج”M—ت‚ًŒn‚ة‹zژû‚·‚邽‚كپAٹOٹE‚ة‚¢‚éژ„‚½‚؟‚ح—â‹pŒّ‰ت‚ً“¾‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB‚±‚ج‚و‚¤‚ةپAٹOٹE‚ج”M‚ًŒn‚ة‹zژû‚µ‚ب‚ھ‚çگi‚ق”½‰‚ًپu‹z”M”½‰(endothermic reaction)پv‚ئ‚¢‚¢‚ـ‚·پB
(ii) ”M‰»ٹw•û’ِژ®
•¨ژ؟‚حپAŒ‹چ‡‚âڈَ‘ش‚ةٹî‚أ‚¢‚½پA‚»‚ꂼ‚êŒإ—L‚جƒGƒlƒ‹ƒMپ[‚ًژ‚ء‚ؤ‚¢‚ـ‚·پB‚»‚ج‚½‚كپA‰»ٹw•د‰»‚ة‚و‚ء‚ؤ•¨ژ؟‚ھ•د‰»‚·‚é‚ئپA•¨ژ؟‚ج•غ—L‚·‚éƒGƒlƒ‹ƒMپ[‚à•د‰»‚µپAٹOٹE‚ئ‚جٹش‚إپAƒGƒlƒ‹ƒMپ[‚جڈo“ü‚è‚ھ‹N‚±‚è‚ـ‚·پB‚±‚ج‚و‚¤‚ة”½‰‚ة”؛‚ء‚ؤڈo“ü‚è‚·‚éƒGƒlƒ‹ƒMپ[‚ًپAپu”½‰”M(heat of reaction)پv‚ئ‚¢‚¢‚ـ‚·پB‚ـ‚½پAژں‚ج‚و‚¤‚ةپA‰»ٹw”½‰ژ®‚ج‰E•س‚ئچ¶•س‚ً“™چ†‚إŒ‹‚رپA‰E•س‚ة”½‰”M‚ًڈ‘‚«‰ء‚¦‚½‚à‚ج‚ًپAپu”M‰»ٹw•û’ِژ®(thermochemical equation)پv‚ئ‚¢‚¢‚ـ‚·پB
C2H4(‹C)پ@پ{پ@3O2(‹C)پ@پپپ@2CO2(‹C)پ@پ{پ@2H2O(‰t)پ@پ{پ@1,412 kJ
”M‰»ٹw•û’ِژ®‚ة‚¨‚¯‚鉻ٹwژ®‚حپA•¨ژ؟‚جژي—ق‚ً•\‚·‚ئ‚ئ‚à‚ةپAٹe•¨ژ؟1 mol‚ج•غ—L‚·‚éƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[’l‚ًˆس–،‚µ‚ـ‚·پB‚ـ‚½پA‰»ٹwژ®‚جŒWگ”‚حپA•¨ژ؟‚جƒ‚ƒ‹گ”‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB‚³‚ç‚ةپAŒإ‘جپE‰t‘جپE‹C‘ج‚ب‚ا‚ج•¨ژ؟‚جڈَ‘ش‚ة‚و‚ء‚ؤپA•غ—L‚·‚éƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ج’l‚ھˆظ‚ب‚邽‚ك‚ةپAŒ´‘¥‚ئ‚µ‚ؤ‰»ٹwژ®‚ج‚ ‚ئ‚ة•¨ژ؟‚جڈَ‘ش‚ًڈ‘‚«“Y‚¦‚ـ‚·پB•¨ژ؟‚جڈَ‘ش‚حپAپu‹C‘ج(gas)پv‚ح(‹C)‚ـ‚½‚ح(g)پAپu‰t‘ج(liquid)پv‚ح(‰t)‚ـ‚½‚ح(l)پAپuŒإ‘ج(solid)پv‚ح(Œإ)‚ـ‚½‚ح(s)‚ج‚و‚¤‚ةڈ‘‚«‚ـ‚·پB‚½‚¾‚µپA‚»‚جڈَ‘ش‚ھ–¾‚ç‚©‚بڈêچ‡‚ة‚حپAڈَ‘ش‚ج•\ژ¦‚ًڈب—ھ‚·‚邱‚ئ‚à‚إ‚«‚ـ‚·پB‚ـ‚½پA“¯‘f‘ج‚ھ‘¶چف‚·‚é’Y‘fC‚ب‚ا‚جڈêچ‡‚ة‚حپA(چ•‰”)‚â(ƒ_ƒCƒ„ƒ‚ƒ“ƒh)‚ب‚ا‚جڈَ‘ش‚ًڈ‘‚«“Y‚¦‚é‚و‚¤‚ة‚µ‚ـ‚·پB
”M‰»ٹw•û’ِژ®‚حپA”½‰•¨‚ئگ¶گ¬•¨‚جƒGƒlƒ‹ƒMپ[ٹضŒW‚ًژ¦‚µ‚½•û’ِژ®‚إ‚·پB”½‰”M‚ج•„چ†‚حپA””M”½‰‚إ‚حƒvƒ‰ƒXپA‹z”M”½‰‚إ‚حƒ}ƒCƒiƒX‚ة‚ب‚è‚ـ‚·پBˆê”ت“I‚ةپA•¨ژ؟‚جƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ھ‘ه‚«‚¢‚ظ‚اپA”½‰گ«‚ھچ‚‚•sˆہ’è‚بڈَ‘ش‚ة‚ب‚é‚ج‚إپAژ©گg‚جƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ً”MƒGƒlƒ‹ƒMپ[‚ئ‚µ‚ؤ•ْڈo‚µ‚ؤپAگ¶گ¬•¨‚جƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ھ’ل‚‚ب‚é””M”½‰‚ج•û‚ھپAگ¶گ¬•¨‚جƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ھچ‚‚‚ب‚é‹z”M”½‰‚و‚è‚àژ©‘R‚ة‹N‚±‚è‚â‚·‚¢‚إ‚·پB
(2) ƒGƒ“ƒ^ƒ‹ƒsپ[‚ئƒGƒ“ƒgƒچƒsپ[
(i) “à•”ƒGƒlƒ‹ƒMپ[
پ@•¨ژ؟‚جچ\گ¬—±ژq‚حپA”M‰^“®‚ة‚و‚é‰^“®ƒGƒlƒ‹ƒMپ[‚ًژ‚ء‚ؤ‚¢‚ـ‚·پB‚ـ‚½پA‚±‚ê‚ç‚ج—±ژq‚حپAŒف‚¢‚ة—ح‚ً‹y‚ع‚µچ‡‚¢پA—±ژqٹش‚ج—ح‚ة‚و‚éˆت’uƒGƒlƒ‹ƒMپ[‚ًژ‚ء‚ؤ‚¢‚ـ‚·پB‚±‚ê‚ç‚جƒGƒlƒ‹ƒMپ[‚ج‘چکa‚ًپA•¨ژ؟‚جپu“à•”ƒGƒlƒ‹ƒMپ[(internal energy)پv‚ئ‚¢‚¢‚ـ‚·پB“à•”ƒGƒlƒ‹ƒMپ[‚حƒGƒlƒ‹ƒMپ[‚جژںŒ³‚ًژ‚؟پA‹Lچ†U‚إ•\‚³‚ê‚ـ‚·پB“à•”ƒGƒlƒ‹ƒMپ[U‚حپA‚»‚جˆ³—ح‚â‘جگد‚ةٹضŒW‚ب‚پA•¨ژ؟—ت‚ئ‰·“x‚¾‚¯‚إŒˆ‚ـ‚è‚ـ‚·پB•¨ژ؟‚ج‰·“xT‚ھچ‚‚¢‚ظ‚اپA—±ژq‚ج”M‰^“®‚حŒƒ‚µ‚‚ب‚èپA“à•”ƒGƒlƒ‹ƒMپ[U‚ح‘ه‚«‚‚ب‚è‚ـ‚·پB
پ@•¨ژ؟‚ج“à•”ƒGƒlƒ‹ƒMپ[U‚حپAٹOٹE‚©‚ç‰ء‚¦‚ç‚ê‚é”MQ‚âٹOٹE‚©‚炳‚ê‚éژdژ–W‚ة‚و‚ء‚ؤ•د‰»‚µ‚ـ‚·پB‚±‚ج‚ئ‚«پAŒn‚ة‰ء‚¦‚ç‚ꂽ”M—تQ‚ئٹOٹE‚©‚炳‚ꂽژdژ–W‚جکa‚حپAŒn‚ج“à•”ƒGƒlƒ‹ƒMپ[•د‰»ƒ¢U‚ئ“™‚µ‚‚ب‚è‚ـ‚·پB‚±‚ê‚ًپu”M—حٹw‘وˆê–@‘¥(first law of thermodynamics)پv‚ئ‚¢‚¢پA‚±‚ج–@‘¥‚حپuƒGƒlƒ‹ƒMپ[‚ج•غ‘¶پv‚ً•\‚·–@‘¥‚ج1‚آ‚إ‚·پB‚ب‚¨پA”M‚ئژdژ–‚جŒü‚«‚ة‚آ‚¢‚ؤپAگ³‚جŒü‚«‚ً‚ا‚؟‚ç‚ئ‚·‚é‚©‚ح•¶Œ£‚ة‚و‚ء‚ؤ—lپX‚إ‚·پB‚±‚±‚إ‚حپA”M‚ئژdژ–‚جŒü‚«‚ًپAپuٹOٹE‚©‚çŒn‚ةŒü‚©‚¤•ûŒüپv‚ًگ³‚ئ‚µ‚ؤ‚¢‚ـ‚·پB
![]()
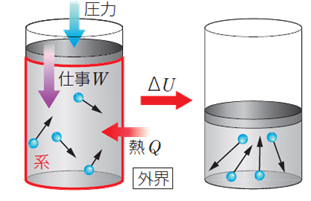
گ}.1 “à•”ƒGƒlƒ‹ƒMپ[‚ئ”M—حٹw‘وˆê–@‘¥
‚ب‚¨پAŒn‚ج‘جگد‚ًˆê’è‚ة‚·‚éڈًŒڈ(“™گد‰ك’ِ)‚إ‚حپAٹOٹE‚©‚炳‚ê‚éژdژ–W‚ح0‚ة‚ب‚è‚ـ‚·پB‚±‚ج‚و‚¤‚ب“™گد‰ك’ِ‚إ‚حپAٹOٹE‚©‚ç”M‚ً‰ء‚¦‚é‚ئپA‚»‚ج‚·‚ׂؤ‚ھ“à•”ƒGƒlƒ‹ƒMپ[‚جڈمڈ¸‚ةژg‚ي‚ê‚邱‚ئ‚ة‚ب‚è‚ـ‚·پB‚آ‚ـ‚èپA‘جگدˆê’è‚جڈًŒڈ‚ب‚ç‚خپA“à•”ƒGƒlƒ‹ƒMپ[•د‰»ƒ¢U‚حپAŒn‚ة‰ء‚¦‚ç‚ꂽ”MQ‚»‚ج‚à‚ج‚ة‚ب‚è‚ـ‚·پB
![]()
‚½‚¾‚µپA‰»ٹw”½‰‚ًچl‚¦‚éچغ‚حپA‚ا‚؟‚ç‚©‚ئ‚¢‚¤‚ئپA“™گد‰ك’ِ‚و‚è‚à“™ˆ³‰ك’ِ(ˆ³—ح‚ًˆê’è‚ة‚·‚éڈًŒڈ)‚ج•û‚ھ‘½‚¢‚إ‚·پBƒrپ[ƒJپ[‚ج’†‚إ”½‰‚ھ‹N‚±‚é‚ئ‚«پA‹َ‹C’†‚إ”½‰‚ھ‹N‚±‚é‚ئ‚«‚ب‚ا‚حپA‚¢‚¸‚ê‚àٹJ•ْŒn‚إ‚ج”½‰‚ب‚ج‚إپAˆ³—ح‚حڈي‚ة‘ه‹Cˆ³‚ئ“™‚µ‚¢‚إ‚·پBˆ³—حˆê’è‚جڈًŒڈ‚إ”M‚ً•\‚µ‚½‚¢‚ئ‚«‚ة—p‚¢‚é‚ج‚ھپAژںچ€‚جپuƒGƒ“ƒ^ƒ‹ƒsپ[پv‚ب‚ج‚إ‚·پB
(ii) ƒGƒ“ƒ^ƒ‹ƒsپ[
پ@پuƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy)پv‚ئ‚حپA•¨ژ؟‚ج””M‚â‹z”M‚ج‹““®‚ةٹض‚ي‚éڈَ‘ش—ت‚إ‚·پBƒMƒٹƒVƒAŒê‚جپu‰·‚ـ‚é(enthalpein)پv‚ة—R—ˆ‚µ‚ؤ‚¨‚èپAپu”Mٹـ—ت(heat content)پv‚ئ‚à‚¢‚¢‚ـ‚·پBŒn‚ةٹOٹE‚©‚ç”M‚ً‰ء‚¦‚é‚ئپAŒn‚ج“à•”ƒGƒlƒ‹ƒMپ[‚ح‘‘ه‚µ‚ـ‚·‚ھپA‰ء‚¦‚ç‚ꂽ”M‚جˆê•”‚حپA‹C‘ج‚ج–c’£‚جژdژ–‚ةژg‚ي‚ê‚ؤ‚µ‚ـ‚¢‚ـ‚·پB‚±‚ج–c’£‚ةژg‚ي‚ꂽژdژ–‚جƒGƒlƒ‹ƒMپ[‚ً“à•”ƒGƒlƒ‹ƒMپ[‚ة‰ء‚¦‚½‚à‚ج‚ھپAƒGƒ“ƒ^ƒ‹ƒsپ[‚إ‚·پBƒGƒ“ƒ^ƒ‹ƒsپ[H‚حƒGƒlƒ‹ƒMپ[‚جژںŒ³‚ًژ‚؟پA“à•”ƒGƒlƒ‹ƒMپ[‚ًUپAˆ³—ح‚ًPپA‘جگد‚ًV‚ئ‚·‚é‚ئپAƒGƒ“ƒ^ƒ‹ƒsپ[H‚حژں‚ج‚و‚¤‚ة’è‹`‚³‚ê‚ـ‚·پB
![]()
پ@‰»ٹw”½‰‚حپA‘ه‹Cˆ³‰؛‚ب‚ا‚ج‚و‚¤‚ةˆ³—ح‚ًˆê’è‚ة‚·‚éڈًŒڈ(“™ˆ³‰ك’ِ)‚إچl‚¦‚邱‚ئ‚ھ‘½‚¢‚إ‚·پB‚»‚±‚إپAˆ³—حP‚ً’èگ”‚ئŒ©‚ب‚µ‚ؤپA”½‰‘OŒم‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»(”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[)ƒ¢H‚ًچl‚¦‚é‚ئپAƒ¢Hپپƒ¢Uپ{Pƒ¢V ‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB—ل‚¦‚خپAŒn‚ةQپپ500 J‚ج”M‚ً‰ء‚¦‚½‚ئ‚«پAٹO•”‚ضWoutپپ100 J‚جژdژ–‚ً‚µ‚½ڈêچ‡‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»‚حپAƒ¢H پپ400پ{100پپ500 J‚ئ‚ب‚è‚ـ‚·پB
![]()
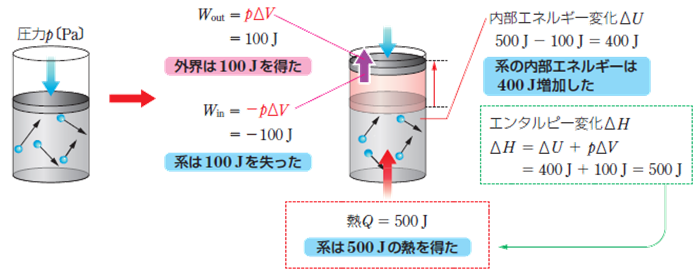
گ}.2 ƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ج‹پ‚ك•û
‚ب‚¨پAŒn‚ة‰ء‚¦‚ç‚ꂽ”M‚ًQپAŒn‚ة‰ء‚¦‚ç‚ꂽژdژ–‚ًWin‚ئ‚·‚é‚ئپA“à•”ƒGƒlƒ‹ƒMپ[•د‰»ƒ¢U‚حƒ¢UپپQپ{Win‚ج‚و‚¤‚ة•\‚³‚ê‚ـ‚·پB‚ـ‚½پA“™ˆ³‰ك’ِ‚إ‚حPƒ¢V‚حپuٹOٹE‚ة‚µ‚½ژdژ–پv‚ج‚±‚ئ‚ب‚ج‚إپAPƒ¢Vپپ-Win‚جٹضŒW‚ھگ¬—§‚µ‚ـ‚·(‰ء‚¦‚ç‚ꂽژdژ–Win‚جŒü‚«‚ئ‹t)پB‚±‚ê‚و‚èپAڈم‹L‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚جژ®(ƒ¢Hپپƒ¢Uپ{Pƒ¢V)‚ةƒ¢UپپQپ{Win‚ئPƒ¢Vپپ-Win‚ً‘م“ü‚·‚é‚ئپA“™ˆ³ڈًŒڈ‰؛‚إ‚حپAŒn‚ةڈo“ü‚è‚·‚é”MQ‚حپAƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ة“™‚µ‚‚ب‚邱‚ئ‚ھ•ھ‚©‚è‚ـ‚·پB
![]()
![]()
پ@‚آ‚ـ‚èپAˆ³—حˆê’è‚جڈًŒڈ‚ب‚ç‚خپAƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»(”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[)ƒ¢H‚حپAŒn‚ة‰ء‚¦‚ç‚ꂽ”MQ‚»‚ج‚à‚ج‚ب‚ج‚إ‚·پB“™ˆ³ڈًŒڈ‰؛‚ة‚ ‚éŒn‚ھ””M‚µ‚ؤٹOٹE‚ة”M‚ًڈo‚·‚ئƒGƒ“ƒ^ƒ‹ƒsپ[‚ح‰؛‚ھ‚èپA‹z”M‚µ‚ؤٹOٹE‚و‚è”M‚ًژَ‚¯ژو‚é‚ئƒGƒ“ƒ^ƒ‹ƒsپ[‚حڈم‚ھ‚è‚ـ‚·پBˆê’舳—ح‰؛‚إ‚حپA‰»ٹwƒGƒlƒ‹ƒMپ[‚ج•د‰»‚حƒGƒ“ƒ^ƒ‹ƒsپ[‚ج•د‰»ƒ¢H‚ة“™‚µ‚‚ب‚é‚ج‚إ‚·پB—ل‚ئ‚µ‚ؤپA‰–‰»گ…‘fHCl‚ئگ…ژ_‰»ƒiƒgƒٹƒEƒ€NaOH‚ج’†کa”½‰‚ًچl‚¦‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
HClپ@پ{پ@NaOHپ@پ¨پ@NaClپ@پ{پ@H2O
‚±‚ج’†کa”½‰‚حٹOٹE‚ة”M‚ً•ْڈo‚·‚é””M”½‰‚إ‚ ‚èپA”½‰‚ج‰ك’ِ‚إٹOٹE‚ةƒGƒlƒ‹ƒMپ[‚ً57
kJ/mol‚¾‚¯•ْڈo‚µ‚ـ‚·پB‚آ‚ـ‚èپAˆ³—حˆê’è‚جڈًŒڈ‚ب‚ç‚خپA””M‚µ‚ؤٹOٹE‚ة”M‚ً•ْڈo‚µ‚½•ھ(57 kJ/mol)‚¾‚¯پAگ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() ‚حپA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[
‚حپA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() ‚و‚èڈ¬‚³‚‚ب‚é‚ح‚¸‚إ‚·پB‚µ‚½‚ھ‚ء‚ؤپAگ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[
‚و‚èڈ¬‚³‚‚ب‚é‚ح‚¸‚إ‚·پB‚µ‚½‚ھ‚ء‚ؤپAگ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() ‚حپA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[
‚حپA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() ‚و‚è‚àڈ¬‚³‚‚ب‚è‚ـ‚·پBƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»(”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[)ƒ¢H‚ئ‚حپA”½‰Œn‚ئگ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[چ·‚ب‚ج‚إپA‚±‚ج’†کa”½‰‚جƒ¢H‚ًژ®‚إ•\‚·‚ئپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
‚و‚è‚àڈ¬‚³‚‚ب‚è‚ـ‚·پBƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»(”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[)ƒ¢H‚ئ‚حپA”½‰Œn‚ئگ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[چ·‚ب‚ج‚إپA‚±‚ج’†کa”½‰‚جƒ¢H‚ًژ®‚إ•\‚·‚ئپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
ƒ¢H پپ (گ¶گ¬Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() ) - (”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[
) - (”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[![]() )
)
پˆ ƒ¢H پپ (NaCl‚ئH2O‚جƒGƒ“ƒ^ƒ‹ƒsپ[H ) - (HCl‚ئNaOH‚جƒGƒ“ƒ^ƒ‹ƒsپ[H )
‚±‚ê‚و‚èپA‚±‚ج’†کa”½‰‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ً‹پ‚ك‚é‚ئپAƒ¢Hپپ-57 kJ‚ة‚ب‚è‚ـ‚·پB‚آ‚ـ‚èپAƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚حپAƒ¢Hپƒ0‚ب‚ç””M”½‰‚إ‚ ‚èپAƒ¢Hپ„0‚ب‚ç‹z”M”½‰‚ب‚ج‚إ‚·پBƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚حپA”½‰‚ھ‹N‚±‚ء‚½چغ‚ةŒn‚ئٹOٹE‚ًڈo“ü‚è‚·‚锽‰”M(””M‚ب‚çگ³پA‹z”M‚ب‚畉‚ج•„چ†)‚ئ“¯‚¶گ”’l‚ة‚ب‚è‚ـ‚·‚ھپA”½‰”M‚ئ‚ح•„چ†‚ھ‹t‚ة‚ب‚é‚ج‚إ’چˆس‚ھ•K—v‚إ‚·پBˆ³—حˆê’è‚جڈًŒڈ(ٹJ•ْ‚³‚ꂽ‰»ٹw”½‰Œn)‚ب‚ç‚خپA”½‰”M‚جگ³•‰‚ً‹t‚ة‚µ‚½گ”’l‚ھپA‚»‚ج”½‰‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ة‚ب‚è‚ـ‚·پB
•\.3 ”½‰”M‚ئƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚جٹضŒW
|
|
””M”½‰ |
‹z”M”½‰ |
|
ٹOٹE‚ج‰·“x |
”M‚ً•ْڈo‚µ‚ؤڈمڈ¸‚·‚é |
”M‚ً‹zژû‚µ‚ؤ‰؛چ~‚·‚é |
|
”½‰”M |
•„چ†‚حگ³‚إ•\‚· |
•„چ†‚ح•‰‚إ•\‚· |
|
Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[ |
”M‚ً•ْڈo‚µ‚ؤ‰؛چ~‚·‚é
|
”M‚ً‹zژû‚µ‚ؤڈمڈ¸‚·‚é
|
(iii) ƒGƒ“ƒgƒچƒsپ[
پuƒGƒ“ƒgƒچƒsپ[(entropy)پv‚ئ‚حپAŒn‚ج—گژG‚³‚جژw•W‚ئ‚ب‚éڈَ‘شٹضگ”‚ج‚±‚ئ‚إ‚·پBƒGƒ“ƒgƒچƒsپ[S‚حپAƒGƒlƒ‹ƒMپ[‚ً‰·“x‚إٹ„‚ء‚½ژںŒ³‚ًژ‚؟پASI’PˆتŒn‚إ‚حJ/K‚جژںŒ³‚إ‚·پB‰·“xT‚جŒn‚ة”÷ڈ¬‚ج”Mƒ¢Q‚ً‰آ‹t“I‚ة‰ء‚¦‚½‚ئ‚«‚جƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‚حپAژں‚ج‚و‚¤‚ة•\‚³‚ê‚ـ‚·پB‚±‚جژ®‚ھˆس–،‚·‚邱‚ئ‚حپAƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‚حپA‰ء‚¦‚ç‚ꂽ”M—تQ‚ھ‘ه‚«‚پA‚©‚آ‚»‚جŒn‚ج‰·“xT‚ھ’ل‚¢‚ظ‚اپAƒGƒ“ƒgƒچƒsپ[‚ج‘Œ¸‚ة—^‚¦‚é‰e‹؟‚ھ‘ه‚«‚‚ب‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB
![]()
Œا—§Œn‚ة‚¨‚¢‚ؤپAژ©”“I‚ة‹N‚±‚éژ©‘R•د‰»‚حپA•K‚¸ƒGƒ“ƒgƒچƒsپ[S‚ج‘‘ه‚·‚é•ûŒü‚ةگiچs‚µ‚ؤ‚¢‚«‚ـ‚·پB‚±‚ج‚±‚ئ‚حپA”M—حٹw‘و“ٌ–@‘¥‚إ‚àپAپu‰آ‹t”½‰‚إ‚حƒGƒ“ƒgƒچƒsپ[S‚حˆê’è‚إ‚ ‚èپA•s‰ء‹t”½‰(ژ©”“I•د‰»)‚إ‚حƒGƒ“ƒgƒچƒsپ[S‚ح‘‰ء‚·‚éپv‚ئ•\Œ»‚³‚ê‚ؤ‚¢‚ـ‚·پBŒا—§Œn‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢S‘SپAŒn‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢SŒnپAٹOٹE‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢SٹO‚ئ‚·‚é‚ئپAژ©”“I‚ة‹N‚±‚锽‰‚إ‚حپAژں‚جٹضŒW‚ھگ¬‚è—§‚؟‚ـ‚·پB‚ب‚¨پAŒا—§Œn‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ھƒ¢S‘Sپپ0‚ج‚ئ‚«‚حپA•د‰»‚ح‰آ‹t“I‚إپA‚ا‚؟‚ç‚ج•ûŒü‚ة‚àگi‚ق‚±‚ئ‚ھ‚إ‚«‚ـ‚·پB
![]()
‚ـ‚½پAŒn‚ج—گژG‚³‚حپAˆê”ت“I‚ةپu”z’u‚ج‘½—lگ«پv‚ئپuچs“®‚جƒGƒlƒ‹ƒMپ[پv‚جگد‚إ•\‚·‚±‚ئ‚ھ‚إ‚«‚ـ‚·پB—گژG‚³‚ئ‚حپAŒ¾—t‚جƒCƒپپ[ƒW’ت‚èپA•¨ژ؟‚ًچ\گ¬‚µ‚ؤ‚¢‚é”÷—±ژq‚ھپAƒoƒ‰ƒoƒ‰‚ةژU‚ç‚خ‚ء‚ؤ‚¢‚éڈَ‘ش‚ج‚±‚ئ‚إ‚·پB”÷—±ژq‚ً‚«‚؟‚ٌ‚ئگ®—گ®“ع‚µ‚ؤ‚¨‚‚و‚èپAƒoƒ‰ƒoƒ‰‚ةژU‚ç‚خ‚ء‚½ڈَ‘ش‚ة‚µ‚ؤ‚¨‚•û‚ھپAƒGƒlƒ‹ƒMپ[“I‚ةˆہ’è‚ب‚ج‚إ‚·پB‚±‚ج—گژG‚³‚ً•\‚·ژ®‚ة‚¨‚¢‚ؤپAƒGƒ“ƒgƒچƒsپ[S‚حپA”z’u‚ج‘½—lگ«‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB
—گژG‚³پپ(”z’u‚ج‘½—lگ«)پ~(چs“®‚جƒGƒlƒ‹ƒMپ[)
—گژG‚³‚حپAƒGƒ“ƒgƒچƒsپ[S‚ج‘ه‚«‚³‚ة”ن—ل‚·‚é‚ج‚إپAƒGƒ“ƒgƒچƒsپ[S‚ھ‘ه‚«‚¢(”÷—±ژq‚ج”z’u‚جژd•û‚ھ‘½—l‚ة‚ب‚é)‚ظ‚اپA—گژG‚³‚ح‘ه‚«‚‚ب‚è‚ـ‚·پB‚ـ‚½پA”÷—±ژq‚جچs“®‚جƒGƒlƒ‹ƒMپ[‚ھ‘ه‚«‚¢‚ظ‚اپA”÷—±ژq‚ج”z’u‚ًژںپX‚ئ•د‚¦‚ؤ‚¢‚‚±‚ئ‚ھ‚إ‚«‚é‚ج‚إپA—گژG‚³‚ح‘ه‚«‚‚ب‚è‚ـ‚·پB‚آ‚ـ‚èپA—±ژq‚ج”M‰^“®‚ھŒƒ‚µ‚‚ب‚éچ‚‰·‚ج•û‚ھپA—گژG‚³‚ح‘ه‚«‚‚ب‚è‚ـ‚·پBژں‚ة—گژG‚³‚ھ‘‰ء‚·‚锽‰(ƒ¢Sپ„0)‚ج—ل‚ًژ¦‚µ‚ـ‚·پB
|
‡@ —±ژqگ”‚ھ‘‰ء‚·‚锽‰پ@پ@2N2O5پ@پ¨پ@4NO2پ@پ{پ@O2 ‡A ‚و‚è‹َٹش‚ج‘½‚¢ڈَ‘ش‚ض‚ج•د‰»پ@پ@H2O(‰t‘ج)پ@پ¨پ@H2O(‹C‘ج) ‡B ‰^“®‚جژ©—R“x‚ج‘½‚¢ڈَ‘ش‚ض‚ج•د‰»پ@پ@H2O(Œإ‘ج)پ@پ¨پ@H2O(‰t‘ج) ‡C ‘g‚فچ‡‚ي‚¹‚ج‘½—l‚ب•ھژq‚ض‚ج•د‰»پ@پ@(H-H, I-I)پ@پ¨پ@(H-I, H-I) ‡D ‚و‚èچ¬چ‡‚µ‚½ڈَ‘ش‚ض‚ج•د‰»پ@پ@گ…پ@پ{پ@ƒGƒ^ƒmپ[ƒ‹پ@پ¨پ@چ¬چ‡•¨ |
پ@‚ ‚鉻ٹw”½‰‚ھژ©‘R‚ةگiچs‚·‚é‚©‚ا‚¤‚©‚حپAŒn‚جƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ئƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‚ج‘ه‚«‚³‚إŒˆ‚ـ‚è‚ـ‚·پBٹî–{“I‚ة‚حپAŒn‚ج‰»ٹwƒGƒlƒ‹ƒMپ[‚ھ’ل‰؛‚·‚é””M”½‰(ƒ¢Hپƒ0)‚ج•û‚ھپA‹z”M”½‰(ƒ¢Hپ„0)‚و‚è‚à‹N‚±‚è‚â‚·‚¢‚ئچl‚¦‚ؤ—ا‚¢‚إ‚µ‚ه‚¤پB‚µ‚©‚µپAŒn‚ج‰»ٹwƒGƒlƒ‹ƒMپ[‚ھڈمڈ¸‚·‚é‹z”M”½‰(ƒ¢Hپ„0)‚إ‚àپA—گژG‚³‚ھ‘‘ه‚·‚锽‰(ƒ¢Sپ„0)‚جڈêچ‡‚ة‚حپAژ©‘R‚ة”½‰‚ھگiچs‚·‚邱‚ئ‚ھ‚ ‚è‚ـ‚·پB“ء‚ةƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‚حپA‰·“x‚ھچ‚‚‚ب‚é‚ظ‚ا‰e‹؟‚ً‹‚ژَ‚¯‚é‚ج‚إپAچ‚‰·‚إ‚ح—گژG‚³‚ھ‘‘ه‚·‚锽‰(ƒ¢Sپ„0)‚ھ‹N‚±‚è‚â‚·‚‚ب‚è‚ـ‚·پB‚ ‚鉻ٹw”½‰‚ھ‹N‚±‚é‚©‚ا‚¤‚©‚حپAژںچ€‚جپuƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[پv‚ًچl‚¦‚邱‚ئ‚إ”»’f‚·‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
(iv) ƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[
پ@“™‰·“™ˆ³‰ك’ِ‚إپA‚ ‚éŒا—§Œn(Œn‚جژü‚è‚ةٹOٹE‚ھ‚ ‚é)‚ج‰»ٹw•د‰»‚ًچl‚¦‚ؤ‚ف‚ـ‚·پB”M—حٹw‘و“ٌ–@‘¥‚ة‚و‚é‚ئپAŒا—§Œn‚إ‹N‚±‚éژ©”“I•د‰»‚حپA•K‚¸ƒGƒ“ƒgƒچƒsپ[S‚ھ‘‘ه‚·‚é•ûŒü‚ةگi‚ف‚ـ‚·پB‚»‚ج‚½‚كپAŒا—§Œn‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢S‘SپAŒn‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢SپAٹOٹE‚جƒGƒ“ƒgƒچƒsپ[•د‰»‚ًƒ¢SٹO‚ئ‚·‚é‚ئپAژ©”“I‚ة‹N‚±‚锽‰‚إ‚حپAژں‚جٹضŒW‚ھگ¬‚è—§‚؟‚ـ‚·پB
![]()
پ@”M—حٹw‘و“ٌ–@‘¥‚إ—‰ً‚ھ“‚¢‚ج‚حپAٹOٹE‚جƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢SٹO‚إ‚·پBٹOٹE‚جƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢SٹO‚حپA‚»‚ج‚ئ‚«‚ج”½‰‰·“x‚âˆع“®‚µ‚½”M—ت‚ة‚و‚ء‚ؤ•د‰»‚·‚é‚©‚ç‚إ‚·پB‚»‚±‚إپAژ©”“I‚ب•د‰»‚جŒü‚«‚ج”»•ت‚ًچs‚¤چغ‚ةپAٹOٹE‚ج‚±‚ئ‚ًچl‚¦‚¸‚ةچد‚فپAŒn‚ة‚آ‚¢‚ؤ‚¾‚¯چl‚¦‚ê‚خ‚و‚¢‚و‚¤‚ة“±“ü‚³‚ꂽ‚ج‚ھپAپuƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[(Gibbs' free energy)پv‚إ‚·پBƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[‚حپAژں‚ج‚و‚¤‚ة”M—حٹw‘و“ٌ–@‘¥‚جژ®‚©‚瓱ڈo‚·‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
پ@‰·“x‚ئˆ³—ح‚ًˆê’è‚ة•غ‚ء‚½Œn‚إپAژ©”“I‚ة”½‰‚ھ‹N‚±‚èپAٹOٹE‚ة”M‚ھ•ْڈo‚³‚ꂽ‚ئ‚µ‚ـ‚·پB‚±‚ئ‚ج‚«پAٹOٹE‚جƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢SٹO‚حپAٹOٹE‚©‚çŒn‚ةˆع“®‚·‚é”M‚ًQپAŒn‚ج‰·“x‚ًT‚ئ‚·‚é‚ئپAƒ¢SٹOپپ-Q /T‚ج‚و‚¤‚ة•\‚³‚ê‚ـ‚·پB‚ب‚¨پA‚±‚جژ®‚إ•„چ†‚ھ•‰‚ة‚ب‚é——R‚حپAٹOٹE‚©‚çŒn‚ة”M‚ھˆع“®‚·‚éŒü‚«‚ًگ³‚ئ‚µ‚½‚½‚ك‚إ‚·پB‚ـ‚½پA”M—حٹw‘وˆê–@‘¥‚و‚èپAƒ¢UپپQپ{W‚جٹضŒW‚ھگ¬‚è—§‚آ‚ج‚إپAQپپƒ¢U-W‚ًƒ¢SٹOپپ-Q /T‚ة‘م“ü‚·‚é‚ئپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
![]()
پ@‚ـ‚½پA“™ˆ³ڈًŒڈ‰؛‚إ‚حپAPƒ¢V‚حپuٹOٹE‚ة‚µ‚½ژdژ–پv‚ج‚±‚ئ‚ب‚ج‚إپAŒn‚ة‰ء‚¦‚ç‚ꂽژdژ–W‚حپAWپپ-Pƒ¢V‚ئ•\‚³‚ê‚ـ‚·(ٹOٹE‚ة‚µ‚½ژdژ–‚جŒü‚«‚ئ‹t‚ة‚ب‚è‚ـ‚·)پB‚و‚ء‚ؤپAŒا—§Œn‚جƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‘S‚حپAژں‚ج‚و‚¤‚ة•دŒ`‚إ‚«‚ـ‚·پB
![]()
![]()
![]()
![]()
ڈمژ®‚جUپ{PV-TS‚ج•”•ھ‚ًپuƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[پv‚ئ‚¢‚¢پA‹Lچ†G‚إ•\‚µ‚ـ‚·پB‚±‚ê‚و‚èپA“™‰·“™ˆ³‰ك’ِ‚إ‚حپAژ©”“I•د‰»‚حƒ¢Gپƒ0‚ئ‚ب‚邱‚ئ‚ھ•ھ‚©‚è‚ـ‚·پB‚ـ‚½پAƒGƒ“ƒ^ƒ‹ƒsپ[H‚حپAHپپUپ{PV‚إ•\‚³‚ê‚é‚ج‚إپAƒMƒuƒX‚جژ©—RƒGƒlƒ‹ƒMپ[•د‰»‚حپAƒ¢Gپپƒ¢H-Tƒ¢S‚ج‚و‚¤‚ة•\‚¹‚ـ‚·پB‚±‚جژ®‚ة‚¨‚¢‚ؤپAƒGƒ“ƒgƒچƒsپ[•د‰»ƒ¢S‚ئ‰·“xT‚ھگد‚ة‚ب‚ء‚ؤ‚¢‚é‚ج‚حپA—گژG‚³‚ھ‰·“xT‚ة”ن—ل‚·‚é‚©‚ç‚إ‚·پB‰·“x‚ھڈم‚ھ‚é‚ئپA”÷—±ژq‚جچs“®‚جƒGƒlƒ‹ƒMپ[‚ھ‘ه‚«‚‚ب‚é‚ج‚إپA—گژG‚³‚à‘ه‚«‚‚ب‚é‚ج‚إ‚·پB
![]()
![]()
‰»ٹw”½‰‚ھگiچs‚·‚é‚©‚ا‚¤‚©‚حپAژ©—RƒGƒlƒ‹ƒMپ[•د‰»ƒ¢G‚ج’l‚ة‚©‚©‚ء‚ؤ‚¢‚ـ‚·پBƒ¢Gپƒ0‚ب‚ç‚خ‰»ٹw”½‰‚حگiچs‚µپAƒ¢Gپ„0‚ب‚ç‚خ‰»ٹw”½‰‚حگiچs‚µ‚ـ‚¹‚ٌپB‚½‚ء‚½‚±‚ꂾ‚¯‚ب‚ج‚إ‚·‚ھپAƒ¢G‚ة‚¨‚¯‚é“ئ—§•دگ”‚حپAƒ¢HپEƒ¢SپET‚ج3‚آ‚ھ‚ ‚邽‚كپA‚±‚ê‚ç‚ج’l‚·‚ׂؤ‚ھ•ھ‚©‚ء‚ؤ‚¢‚ب‚¯‚ê‚خپAƒ¢G‚جگ³ٹm‚ب’l‚ًŒˆ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚¹‚ٌپB‚µ‚©‚µ‚ب‚ھ‚çپA‚ ‚鉻ٹw”½‰‚ھ””M“I‚ة‹N‚±‚è(ƒ¢Hپƒ0)پAƒGƒ“ƒgƒچƒsپ[•د‰»‚ھƒ¢Sپ„0‚إ‚ ‚邱‚ئ‚ھ•ھ‚©‚ء‚ؤ‚¢‚é‚ب‚çپAژ©—RƒGƒlƒ‹ƒMپ[•د‰»‚ح•K‘R“I‚ةƒ¢Gپƒ0‚ئ‚ب‚èپAڈ‚ب‚‚ئ‚à‚±‚ج”½‰‚ح‰·“xT‚ة‚و‚炸پAژ©‘R‚ةگiچs‚·‚邱‚ئ‚ھ•ھ‚©‚è‚ـ‚·(ƒ¢H‚ئƒ¢S‚ج•„چ†‚ح”½‰‚جژي—ق‚ة‚و‚è‚ـ‚·‚ھپAT‚ج•„چ†‚ح•K‚¸گ³‚ة‚ب‚é‚©‚ç‚إ‚·)پB‚±‚ج‚و‚¤‚ةƒ¢HپEƒ¢SپET‚ج’l‚ھگ³ٹm‚ة•ھ‚©‚ء‚ؤ‚¢‚ب‚‚ؤ‚àپA”½‰‚ھگiچs‚·‚é‚©‚ا‚¤‚©‚ً”»’f‚·‚éڈp‚ح‚ ‚é‚ج‚إ‚·پBژں‚ج•\.4‚ةپA‰»ٹw”½‰‚ھژ©‘R‚ةگiچs‚·‚é‚©‚ا‚¤‚©‚جپA’èگ«“I‚ب”»’f‚ً—^‚¦‚é•\‚ًژ¦‚µ‚ـ‚·پB
•\.4 ‰»ٹw”½‰‚ھژ©‘R‚ةگiچs‚·‚é‚©‚ا‚¤‚©
|
ƒGƒ“ƒ^ƒ‹ƒsپ[ |
ƒGƒ“ƒgƒچƒsپ[ |
ژ©—RƒGƒlƒ‹ƒMپ[ |
”½‰ |
|
””M”½‰ پiƒ¢Hپƒ0پj |
ƒ¢Sپ„0 |
ƒ¢Gپƒ0 |
ژ©‘R‚ةگiچs‚·‚é |
|
ƒ¢Sپƒ0 |
’ل‰·‚إƒ¢Gپƒ0 |
ژ©‘R‚ةگiچs‚·‚é |
|
|
چ‚‰·‚إƒ¢Gپ„0 |
ژ©‘R‚ةگiچs‚µ‚ب‚¢ |
||
|
‹z”M”½‰ پiƒ¢Hپ„0پj |
ƒ¢Sپ„0 |
’ل‰·‚إƒ¢Gپ„0 |
ژ©‘R‚ةگiچs‚µ‚ب‚¢ |
|
چ‚‰·‚إƒ¢Gپƒ0 |
ژ©‘R‚ةگiچs‚·‚é |
||
|
ƒ¢Sپƒ0 |
ƒ¢Gپ„0 |
ژ©‘R‚ةگiچs‚µ‚ب‚¢ |
‰»ٹw”½‰‚ھژ©‘R‚ةگiچs‚·‚é‚©‚ا‚¤‚©‚حپA‚»‚ج”½‰‚ھ””M”½‰‚©‚ا‚¤‚©پA‚ ‚é‚¢‚ح—گژG‚³‚ھ‘‰ء‚·‚锽‰‚©‚ا‚¤‚©‚جپA2‚آ‚ج—vˆِ‚ة‚و‚ء‚ؤŒˆ’肳‚ê‚ـ‚·پB‚ ‚锽‰‚ھژ©‘R‚ةگiچs‚·‚é‚ئ‚«‚حپAگiچs‚·‚邱‚ئ‚ة‚و‚ء‚ؤŒn‚جƒGƒlƒ‹ƒMپ[‚ھŒ¸ڈ‚·‚é‚©پA‚ ‚é‚¢‚ح—گژG‚³‚ھ‘‰ء‚·‚é‚©پAڈ‚ب‚‚ئ‚à‚ا‚؟‚ç‚©ˆê•û‚ھگ¬‚è—§‚ء‚ؤ‚¢‚ب‚¯‚ê‚خ‚ب‚è‚ـ‚¹‚ٌپB‚»‚ج‚ا‚؟‚ç‚©ˆê•û‚ھ•غڈط‚³‚ê‚ب‚¯‚ê‚خپA”½‰‚ھژ©‘R‚ةگiچs‚·‚邱‚ئ‚ح‚ ‚肦‚ب‚¢‚ج‚إ‚·پB
(v) ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[
‰»ٹw”½‰‚ة”؛‚¤”M‚جڈo“ü‚è‚حپA‰»ٹw”½‰ژ®‚ةƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»ƒ¢H‚ً•t‚µ‚½ژ®‚إژ¦‚·‚±‚ئ‚ھ‚إ‚«‚ـ‚·پB’…–ع‚·‚镨ژ؟‚جŒWگ”‚ھ1‚ة‚ب‚é‚و‚¤‚ة‚µ‚ؤ”½‰ژ®‚ًچى‚é‚ج‚إپA‘¼‚ج•¨ژ؟‚جŒWگ”‚ھ•ھگ”‚ة‚ب‚邱‚ئ‚à‚ ‚è‚ـ‚·پB—ل‚¦‚خپA1 mol‚جگ…‘fH2‚ھٹ®‘S”Rڈؤ‚µ‚ؤپA‰t‘ج‚جگ…H2O‚ھگ¶گ¬‚µپA286 kJ‚ج”M—ت‚ھ•ْڈo‚³‚ê‚锽‰‚حپAژں‚ج‚و‚¤‚ة•\‚³‚ê‚ـ‚·پB
![]()
•¨ژ؟‚جڈَ‘ش‚ة‚و‚èپA•¨ژ؟‚ھژ‚آƒGƒ“ƒ^ƒ‹ƒsپ[‚ھˆظ‚ب‚邽‚كپAŒ´‘¥‚ئ‚µ‚ؤڈمژ®‚ج‚و‚¤‚ة•¨ژ؟‚جڈَ‘ش‚ً–¾‹L‚µ‚ـ‚·پB•¨ژ؟‚جڈَ‘ش‚حپAپu‹C‘ج(gas)پv‚ح(‹C)‚ـ‚½‚ح(g)پAپu‰t‘ج(liquid)پv‚ح(‰t)‚ـ‚½‚ح(l)پAپuŒإ‘ج(solid)پv‚ح(Œإ)‚ـ‚½‚ح(s)‚ج‚و‚¤‚ةڈ‘‚«‚ـ‚·پB‚½‚¾‚µپA‚»‚جڈَ‘ش‚ھ–¾‚ç‚©‚بڈêچ‡‚ة‚حپAڈَ‘ش‚ج•\ژ¦‚ًڈب—ھ‚·‚邱‚ئ‚à‚إ‚«‚ـ‚·پB‚ـ‚½پA“¯‘f‘ج‚ھ‘¶چف‚·‚é’Y‘fC‚ب‚ا‚جڈêچ‡‚ة‚حپA(چ•‰”)‚â(ƒ_ƒCƒ„ƒ‚ƒ“ƒh)‚ب‚ا‚جڈَ‘ش‚ًڈ‘‚«“Y‚¦‚é‚و‚¤‚ة‚µ‚ـ‚·پBگ…‚ة—n‰ً‚µ‚½ڈَ‘ش‚àپA—ل‚¦‚خNaClaq‚ج‚و‚¤‚ةڈ‘‚«‚ـ‚·پB
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA”½‰‚جژي—ق‚ة‚و‚ء‚ؤŒإ—L‚ج–¼ڈج‚إŒؤ‚خ‚ê‚é‚à‚ج‚ھ‚ ‚èپA’…–ع‚·‚镨ژ؟1 mol“–‚½‚è‚ج”M—ت(’PˆتپFkJ/mol)‚إ•\‚³‚ê‚ـ‚·پB’…–ع‚·‚镨ژ؟‚ج‰»ٹw•د‰»‚ج–¼ڈج‚ة‚و‚ء‚ؤپAپuگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy of formation)پv‚âپu”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy of combustion)پvپAپu—n‰ًƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy of dissolution)پvپAپu’†کaƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy of neutralization)پvپAپuگ…کaƒGƒ“ƒ^ƒ‹ƒsپ[(enthalpy of hydration)پv‚ب‚ا‚ھ‚ ‚è‚ـ‚·پB‚ـ‚½پAڈَ‘ش•د‰»‚جچغ‚ةڈo“ü‚è‚·‚é”M‚⌋چ‡ƒGƒlƒ‹ƒMپ[پAƒCƒIƒ“‰»ƒGƒlƒ‹ƒMپ[پA“dژqگeکa—ح‚ب‚ا‚جƒGƒlƒ‹ƒMپ[‚àپA“¯—l‚ة”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚إ•\‚·‚±‚ئ‚ھ‚إ‚«‚ـ‚·پBژں‚ج•\.5‚ة‰»ٹw”½‰‚ة”؛‚¤ƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»‚ً‚ـ‚ئ‚ك‚ـ‚·پB
•\.5 ‰»ٹw”½‰‚ة”؛‚¤ƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»
|
گ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[ |
‰»چ‡•¨1 mol‚ھ‚»‚جگ¬•ھŒ³‘f‚ج’P‘ج‚©‚çگ¶گ¬‚·‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ گ¶گ¬‚·‚鉻چ‡•¨‚جŒWگ”‚ً1‚ة‚·‚é ƒ¢Hپƒ0 (””M)‚جڈêچ‡‚ئƒ¢Hپ„0 (‹z”M)‚جڈêچ‡‚ھ‚ ‚é |
|
exپjNH3‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|46 kJ/mol
|
|
|
”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھٹ®‘S”Rڈؤ‚·‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ”Rڈؤ‚·‚é‰آ”R•¨‚جŒWگ”‚ً1‚ة‚·‚é ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپjCO‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|283 kJ/mol
|
|
|
—n‰ًƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھ‘½—ت‚جگ…‚ة—n‰ً‚·‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ —nژ؟‚جŒWگ”‚ً1‚ة‚·‚é ƒ¢Hپƒ0 (””M)‚جڈêچ‡‚ئƒ¢Hپ„0 (‹z”M)‚جڈêچ‡‚ھ‚ ‚éپiŒإ‘ج‚إ‚حƒ¢Hپ„0 (‹z”M)‚ھ‘½‚¢پj |
|
exپjNaCl(Œإ)‚ج—n‰ًƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H = 4.2 kJ/mol NaCl(Œإ)پ@پ{پ@aqپ@پ¨پ@NaClaqپ@پ@ƒ¢H = 4.2 kJ |
|
|
’†کaƒGƒ“ƒ^ƒ‹ƒsپ[ |
’†کa”½‰‚إ1 mol‚جگ…‚ھگ¶‚¶‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ H2O(‰t)‚جŒWگ”‚ً1‚ة‚·‚é ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپj”–‚¢‹ژ_‚ئ”–‚¢‹‰–ٹî‚ج’†کaƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|56.5 kJ/mol H+aqپ@پ{پ@OHپ|aqپ@پ¨پ@H2O(‰t) پ@پ@ƒ¢H =پ|56.5 kJ |
|
|
گ…کaƒGƒ“ƒ^ƒ‹ƒsپ[ |
‹C‘جڈَ‚جƒCƒIƒ“1 mol‚ھ‘½—ت‚جگ…‚إگ…کa‚³‚ê‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‹C‘جڈَ‚جƒCƒIƒ“‚جŒWگ”‚ً1‚ة‚·‚é ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپjNa+(‹C)‚جگ…کaƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|403 kJ/mol Na+(‹C)پ@پ{پ@aqپ@پ¨پ@Na+aqپ@پ@ƒ¢H =پ|403 kJ |
‚ب‚¨پA”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ًچl‚¦‚éڈêچ‡پAٹ®‘S”Rڈؤ‚ئ‚¢‚¤‚ج‚حپA’Y‘fC‚ح“ٌژ_‰»’Y‘fCO2پAگ…‘fH‚حگ…H2OپA’‚‘fN‚ح’‚‘fN2پA—°‰©S‚ح“ٌژ_‰»—°‰©SO2‚ة•د‰»‚·‚éڈêچ‡‚ًژw‚µ‚ـ‚·پBگ…‘fH‚ھٹ®‘S”Rڈؤ‚µ‚ؤگ…H2O‚ھگ¶گ¬‚·‚éڈêچ‡‚إ‚حپA•پ’ت‚ح‰t‘ج‚ئ‚ب‚é‚ئ‚«‚ج’l‚إژ¦‚µ‚ـ‚·پB
‚ـ‚½پAگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ًچl‚¦‚é‚ئ‚«پAگ¬•ھŒ³‘f‚ج’P‘ج‚ة“¯‘f‘ج‚ھ‚ ‚éڈêچ‡‚ة‚حپAˆہ’è‚ب•û(ƒ|ƒeƒ“ƒVƒƒƒ‹ƒGƒlƒ‹ƒMپ[‚ج’ل‚¢•û)‚ً‘I‚ر‚ـ‚·پB‹ï‘ج“I‚ة‚حپA’Y‘fC‚ب‚çچ•‰”پA—°‰©S‚ب‚çژخ•û—°‰©پAƒٹƒ“P‚ب‚çگشƒٹƒ“‚ج•û‚ھˆہ’è‚إ‚·پB
•\.6 ڈَ‘ش•د‰»‚ة”؛‚¤ƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»
|
ڈِ”ƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھڈِ”‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپ„0 (‹z”M)‚إ‚ ‚é |
|
exپjH2O(‰t)‚جڈِ”ƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H = 44 kJ/mol H2O(‰t)پ@پ¨پ@H2O(‹C) پ@پ@ƒ¢H = 44 kJ |
|
|
‹أڈkƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھ‹أڈk‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپjH2O(‹C)‚ج‹أڈkƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|44 kJ/mol H2O(‹C)پ@پ¨پ@H2O(‰t) پ@پ@ƒ¢H =پ|44 kJ |
|
|
—Z‰ًƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھ—Z‰ً‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپ„0 (‹z”M)‚إ‚ ‚é |
|
exپjH2O(Œإ)‚ج—Z‰ًƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H = 6.0 kJ/mol H2O(Œإ)پ@پ¨پ@H2O(‰t) پ@پ@ƒ¢H = 6.0 kJ |
|
|
‹أŒإƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھ‹أŒإ‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپjH2O(‰t)‚ج‹أŒإƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|6.0 kJ/mol H2O(‰t)پ@پ¨پ@H2O(Œإ) پ@پ@ƒ¢H =پ|6.0 kJ |
|
|
ڈ¸‰طƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھڈ¸‰ط‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپ„0 (‹z”M)‚إ‚ ‚é |
|
exپjH2O(Œإ)‚جڈ¸‰طƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H = 50 kJ/mol H2O(Œإ)پ@پ¨پ@H2O(‹C) پ@پ@ƒ¢H = 50 kJ |
|
|
‹أ‰طƒGƒ“ƒ^ƒ‹ƒsپ[ |
•¨ژ؟1 mol‚ھ‹أ‰ط‚·‚é‚ئ‚«‚ج“]ˆعƒGƒ“ƒ^ƒ‹ƒsپ[ پ¦ ‚·‚ׂؤƒ¢Hپƒ0 (””M)‚إ‚ ‚é |
|
exپjH2O(‹C)‚ج‹أ‰طƒGƒ“ƒ^ƒ‹ƒsپ[پ@ƒ¢H =پ|50 kJ/mol H2O(‹C)پ@پ¨پ@H2O(Œإ‘ج) پ@پ@ƒ¢H =پ|50 kJ |
•\.7 ‚»‚ج‘¼‚ج”½‰‚ة”؛‚¤ƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»
|
Œ‹چ‡ƒGƒlƒ‹ƒMپ[ |
‹C‘ج•ھژq“à2Œ´ژqٹش‚جŒ‹چ‡1 mol‚ًگط‚ء‚ؤپAƒoƒ‰ƒoƒ‰‚جŒ´ژq‚ة‚·‚é‚ج‚ة•K—v‚ب‹z”M—ت |
|
exپjO2‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[پ@ƒ¢H = 498 kJ/mol O2(‹C)پ@پ¨پ@2O(‹C) پ@پ@ƒ¢H = 498 kJ |
|
|
ƒCƒIƒ“‰»ƒGƒlƒ‹ƒMپ[ |
‹C‘جڈَŒ´ژq1 mol‚©‚ç“dژq1 molژو‚ء‚ؤپAˆê‰؟‚ج—zƒCƒIƒ“‚ة‚·‚é‚ج‚ة•K—v‚ب‹z”M—ت |
|
exپjNa‚جƒCƒIƒ“‰»ƒGƒlƒ‹ƒMپ[پ@ƒ¢H = 493 kJ/mol Na(‹C)پ@پ¨پ@Na+(‹C)پ@پ{پ@eپ|پ@پ@ƒ¢H = 493 kJ |
|
|
“dژqگeکa—ح |
‹C‘جڈَŒ´ژq1 mol‚ھ“dژq1 molژَ‚¯ژو‚ء‚ؤپAˆê‰؟‚ج‰AƒCƒIƒ“‚ة‚ب‚é‚ئ‚«‚ة•ْڈo‚³‚ê‚é”M—ت |
|
exپjCl‚ج“dژqگeکa—حپ@ƒ¢H =پ|349 kJ/mol Cl(‹C)پ@پ{پ@eپ|پ@پ¨پ@Clپ|(‹C) پ@پ@ƒ¢H =پ|349 kJ |
(3) ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‹پ‚ك•û
(i) ƒwƒX‚ج–@‘¥
ˆ³—حˆê’è‚جڈًŒڈ‚ة‚¨‚¢‚ؤپA‰»ٹw”½‰‚إڈo“ü‚è‚·‚éƒGƒlƒ‹ƒMپ[‚حپA”½‰•¨‚ئگ¶گ¬•¨‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚جچ·‚إ•\‚³‚ê‚ـ‚·پB—ل‚¦‚خپABپ¨C‚ج”½‰‚ًپA2‚آ‚جˆظ‚ب‚ء‚½ŒoکH(Bپ¨C‚ـ‚½‚حBپ¨Aپ¨C)‚إچs‚ء‚½ڈêچ‡‚ًچl‚¦‚ؤ‚ف‚ـ‚·پB‚µ‚©‚µ‚ب‚ھ‚çپA‚ا‚؟‚ç‚ج”½‰‚àچإڈ‰B‚ئچإŒمC‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ“¯‚¶‚إ‚ ‚èپA‚©‚آ‚ا‚ٌ‚ب‰»ٹw•د‰»‚ة‚¨‚¢‚ؤ‚à‘SƒGƒlƒ‹ƒMپ[‚ح•غ‘¶‚³‚ê‚é‚ج‚إپAچإڈI“I‚بƒGƒ“ƒ^ƒ‹ƒsپ[•د‰»‚ح“¯‚¶‚ة‚ب‚é‚ح‚¸‚إ‚·پB‚»‚µ‚ؤپA‰»ٹw”½‰‚إڈo“ü‚è‚·‚éƒGƒlƒ‹ƒMپ[‚ج‚ظ‚ئ‚ٌ‚ا‚حپA”M‚ئ‚¢‚¤Œ`‘ش‚ًژو‚邽‚ك‚ةپA‰»ٹw•د‰»‚ة”؛‚¤”M‚جژûژx‚حپA‚ا‚ج‚و‚¤‚ب”½‰ŒoکH‚ًژو‚ء‚ؤ‚à“¯‚¶‚ة‚ب‚é‚ج‚إ‚·پB‚±‚ê‚ً”Œ©ژز‚إ‚ ‚éƒچƒVƒA‚ج‰»ٹwژزƒWƒFƒ‹ƒ}ƒ“پEƒAƒ“ƒٹپEƒwƒX‚ج–¼‚ًژو‚ء‚ؤپAپuƒwƒX‚ج–@‘¥(Hessپf law)پv‚ئ‚¢‚¢‚ـ‚·پB
ƒwƒX‚ج–@‘¥‚حپA‚¢‚ي‚خ”M—حٹw‘وˆê–@‘¥(ƒGƒlƒ‹ƒMپ[•غ‘¶‚ج–@‘¥)‚ج‰»ٹw“I‚بŒ¾‚¢ٹ·‚¦‚إ‚·پB‚µ‚©‚µپA”M—حٹw‘وˆê–@‘¥‚ج’ٌڈ¥ˆب‘O‚ة”Œ©‚³‚ꂽ–@‘¥‚ب‚ج‚إپAچ،‚إ‚à‚»‚ج–¼‚ًژc‚µ‚ؤ‚¢‚ـ‚·پB‚ـ‚½پAژں‚جگ}.3‚ج‚و‚¤‚ةپAڈcژ²‚ة•¨ژ؟‚ج•غ—L‚·‚éƒGƒ“ƒ^ƒ‹ƒsپ[‚ًژو‚èپA”½‰•¨‚âگ¶گ¬•¨‚ب‚ا‚جƒGƒ“ƒ^ƒ‹ƒsپ[ٹضŒW‚ً•\‚µ‚½گ}‚ًپAپuƒGƒ“ƒ^ƒ‹ƒsپ[گ}(enthalpy diagram)پv‚ئ‚¢‚¢‚ـ‚·پBƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ة‚¨‚¢‚ؤپA–îˆَ‚ح”½‰‚جŒü‚«‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB‚ـ‚½پAچ‚ƒGƒ“ƒ^ƒ‹ƒsپ[ڈَ‘ش‚©‚ç’لƒGƒ“ƒ^ƒ‹ƒsپ[ڈَ‘ش‚ضŒü‚©‚¤”½‰‚ح””M”½‰(ƒ¢Hپƒ0)پA’لƒGƒ“ƒ^ƒ‹ƒsپ[ڈَ‘ش‚©‚çچ‚ƒGƒ“ƒ^ƒ‹ƒsپ[ڈَ‘ش‚ضŒü‚©‚¤”½‰‚ح‹z”M”½‰(ƒ¢Hپ„0)‚إ‚·پBˆê”ت‚ة•¨ژ؟‚ھƒoƒ‰ƒoƒ‰‚إ‚ ‚é‚ظ‚اچ‚ƒGƒ“ƒ^ƒ‹ƒsپ[‚ة‚ب‚è‚ـ‚·پB
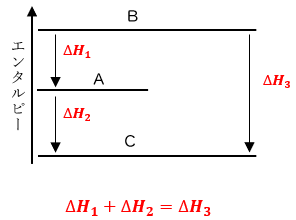
گ}.3 ƒwƒX‚ج–@‘¥‚ئƒGƒ“ƒ^ƒ‹ƒsپ[گ}
(ii) ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج“±ڈo
ƒwƒX‚ج–@‘¥‚ً—p‚¢‚邱‚ئ‚إپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚جŒvژZ‚حپAگ”ٹw‚إٹw‚ش•û’ِژ®‚ئ“¯—l‚جˆµ‚¢‚ھ‚إ‚«‚ـ‚·پB‚±‚ê‚ة‚و‚ء‚ؤپA’¼گع‘ھ’è‚·‚邱‚ئ‚ھچ¢“ï‚ب”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚إ‚àپAٹشگع“I‚ةŒvژZ‚إ‹پ‚ك‚ç‚ê‚é‚و‚¤‚ة‚ب‚é‚ج‚إ‚·پB”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج“±ڈo•û–@‚ًژ¦‚·‘O‚ةپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً•t‚µ‚½”½‰ژ®‚جٹî–{‚ة‚آ‚¢‚ؤپAچؤٹm”F‚µ‚ؤ‚¨‚«‚ـ‚µ‚ه‚¤پB—ل‚ئ‚µ‚ؤپAژں‚ج‰»ٹw”½‰‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ة‚آ‚¢‚ؤچl‚¦‚ؤ‚ف‚ـ‚·پB
aAپ@پ{پ@bBپ@پ¨پ@cCپ@پ{پ@dDپ@پ@پ@ƒ¢H = x kJ
|
‡@ ‰»ٹwژ®‚حپA•¨ژ؟1 mol‚ج•غ—L‚·‚éƒGƒ“ƒ^ƒ‹ƒsپ[’l‚إ‚ ‚éپBŒWگ”a, b, c, d‚ح•¨ژ؟‚جƒ‚ƒ‹گ”‚ً•\‚µپA’تڈي‚ج‰»ٹw”½‰ژ®‚ئˆظ‚ب‚èپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً•\‚·ڈêچ‡‚إ‚ح•ھگ”ŒWگ”‚إ‚ ‚ء‚ؤ‚à‹–‚³‚ê‚éپB ‡A aAپ{bB‚ح”½‰•¨‚جƒGƒ“ƒ^ƒ‹ƒsپ[’l‚ًپAcCپ{dD‚حگ¶گ¬•¨‚جƒGƒ“ƒ^ƒ‹ƒsپ[’l‚ً•\‚·پB‚آ‚ـ‚èپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H = x kJ‚حپA”½‰•¨‚ئگ¶گ¬•¨‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚جچ·‚إ‚ ‚éپB ‡B •¨ژ؟‚ج—ت‚ھ2”{‚ة‚ب‚ê‚خپAƒGƒ“ƒ^ƒ‹ƒsپ[‚à2”{‚ة‚ب‚é‚©‚çپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H = x kJ‚à2”{‚ة‚ب‚éپB‚»‚±‚إپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً•t‚µ‚½‰»ٹw”½‰ژ®‚ً2”{‚µ‚½‚èپA1/2”{‚µ‚½‚肵‚ؤ‚à‚و‚¢پB |
‚±‚ê‚و‚èپAژں‚ج—ل‘è‚ً‰ً‚¢‚ؤ‚ف‚ـ‚µ‚ه‚¤پB’Y‘fC‚ئژ_‘fO2‚©‚çپAˆêژ_‰»’Y‘fCO‚ھگ¶‚¶‚锽‰‚ًچl‚¦‚ؤ‚ف‚ـ‚·پB’Y‘fC‚ً”Rڈؤ‚³‚¹‚½ڈêچ‡پAˆêژ_‰»’Y‘fCO‚ئ“¯ژ‚ة“ٌژ_‰»’Y‘fCO2‚ًگ¶‚¶‚邱‚ئ‚ھ‘½‚پAˆêژ_‰»’Y‘fCO‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ًژہŒ±“I‚ة‹پ‚ك‚邱‚ئ‚حچ¢“ï‚إ‚·پB‚µ‚©‚µپAچ•‰”C‚ئˆêژ_‰»’Y‘fCO‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‚»‚ꂼ‚êژہŒ±‚إگ³ٹm‚ة‹پ‚ك‚ç‚ê‚é‚ج‚إپAˆêژ_‰»’Y‘fCO‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپAژں‚ج‚و‚¤‚ةŒvژZ‚·‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB‚ب‚¨پA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‹پ‚ك•û‚ة‚حپA—lپX‚ب•û–@‚ھ‚ ‚è‚ـ‚·‚ھپA‚±‚±‚إ‚حˆê”ت“I‚ب•û–@‚¾‚¯ژ¦‚µ‚ـ‚·پB
|
پy—ل‘èپz C(چ•‰”)‚ئCO(‹C)‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‚»‚ꂼ‚ꃢH 1=پ|394 kJ/molپAƒ¢H2 =پ|283 kJ/mol‚إ‚ ‚éپB‚±‚ê‚ç‚ج’l‚ً—p‚¢‚ؤپACO(‹C)‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[پkkJ/molپl‚ً‹پ‚ك‚وپB |
(ii-1) ڈء‹ژ–@
ڈء‹ژ–@‚حپAˆê”ت“I‚ب“±ڈo•û–@‚ج1‚آ‚إ‚·پBƒwƒX‚ج–@‘¥‚و‚èپA”½‰•¨پ¨گ¶گ¬•¨‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹پ‚ك‚é‚ج‚ةپA‚ا‚ج‚و‚¤‚ب”½‰ŒoکH‚ًژو‚ء‚ؤ‚à—ا‚©‚ء‚½‚±‚ئ‚ًژv‚¢ڈo‚µ‚ؤ‚‚¾‚³‚¢پB‚ـ‚¸‚حپA‹پ‚ك‚½‚¢”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ًx kJ/mol‚ئ’u‚¢‚ؤپA—^‚¦‚ç‚ꂽ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ًڈ‘‚«ڈo‚µ‚ـ‚·پB
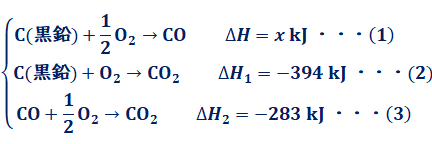
‚±‚ê‚و‚èپA‹پ‚ك‚½‚¢‰»ٹw”½‰ژ®‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA(1)پپ(2)-(3)‚ب‚ج‚إپAگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[x پپپ|111 kJ/mol‚ئ‚¢‚¤‚±‚ئ‚ھ•ھ‚©‚è‚ـ‚·پB
(ii-2) ƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@
ƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@‚حپA•،ژG‚ب”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹پ‚ك‚é‚ج‚ة“K‚µ‚½“±ڈo•û–@‚إ‚·پBˆê”ت“I‚ة‚حپAƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚جڈم•”‚ة‚‚镨ژ؟‚ظ‚اپAƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ‘ه‚«‚¢‚ج‚إپA”½‰گ«‚ھچ‚‚•sˆہ’è‚إ‚·پB‚ـ‚½پA•¨ژ؟‚ھƒoƒ‰ƒoƒ‰‚جڈَ‘ش‚إ‚ ‚é‚ظ‚اپA—±ژq‚ج”M‰^“®‚حŒƒ‚µ‚‚ب‚é‚ج‚إپAƒGƒ“ƒ^ƒ‹ƒsپ[‚ح‘ه‚«‚‚ب‚è‚ـ‚·پB‚»‚êŒج‚ةپAˆê”ت“I‚ة’P‘ج‚⌴ژq‚حƒGƒ“ƒ^ƒ‹ƒsپ[‚ھچإ‚à‘ه‚«‚پA”Rڈؤگ¶گ¬•¨(“ٌژ_‰»’Y‘fCO2‚âگ…H2O‚ب‚ا)‚حƒGƒ“ƒ^ƒ‹ƒsپ[‚ھچإ‚àڈ¬‚³‚¢‚إ‚·پB
‚»‚±‚إپAƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ًچىگ¬‚·‚é‚ئ‚«‚ة‚حپA’P‘ج‚⌴ژq‚ًچإ‚àچ‚ƒGƒ“ƒ^ƒ‹ƒsپ[(ˆê”شڈم)‚ةڈ‘‚«پA”Rڈؤگ¶گ¬•¨‚حچإ‚à’لƒGƒ“ƒ^ƒ‹ƒsپ[(ˆê”ش‰؛)‚ةڈ‘‚‚±‚ئ‚ة‚µ‚ـ‚·پB‚µ‚©‚µپA–â‘è‚ة‚ب‚ء‚ؤ‚¢‚鉻ٹw”½‰‚ھپA””M”½‰(ƒ¢Hپƒ0)‚ب‚ج‚©‹z”M”½‰(ƒ¢Hپ„0)‚ب‚ج‚©‚ھ•ھ‚©‚ء‚ؤ‚¢‚ب‚¢‚ئپAƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ًٹ®گ¬‚³‚¹‚邱‚ئ‚ھ‚إ‚«‚ـ‚¹‚ٌپB‚»‚±‚إپA–â‘è‚ة‚ب‚ء‚ؤ‚¢‚鉻ٹw”½‰‚ًپu””M”½‰(ƒ¢Hپƒ0)پv‚ئ‰¼’肵پAƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ةڈ‘‚«‰ء‚¦‚é‚ج‚إ‚·پB‚»‚µ‚ؤپA‹پ‚ك‚½”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[x‚ھ•‰‚ج’l‚ب‚çپA‰¼’è’ت‚è‚ج””M”½‰(ƒ¢Hپƒ0)‚ئ‚µ‚ؤˆµ‚¢پA‹پ‚ك‚½”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[x‚ھگ³‚ج’l‚ب‚çپA‰¼’è‚ئ‚حˆظ‚ب‚é‹z”M”½‰(ƒ¢Hپ„0)‚ئ‚µ‚ؤˆµ‚¢‚ـ‚·پB
|
”½‰•¨A‚ھگ¶گ¬•¨B‚ة‚ب‚é‚ئ‚« پ@پ@Aپ@پ¨پ@B ‡@ ‹پ‚ك‚锽‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ً””M(ƒ¢Hپƒ0)‚ئ‰¼’è‚·‚é ‡A ’P‘ج‚⌴ژq‚ًˆê”شڈم‚ةڈ‘‚ ‡B ٹ®‘S”Rڈؤگ¶گ¬•¨‚حˆê”ش‰؛‚ةڈ‘‚ ‡C ƒGƒ“ƒ^ƒ‹ƒsپ[چ·‚و‚蔽‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ً‹پ‚ك‚é |
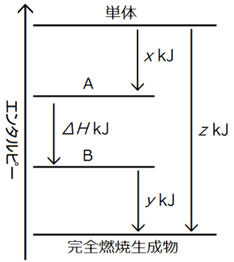
گ}.4پ@ƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@
پ@‚³‚ؤپAƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@‚ً—p‚¢‚ؤپAˆêژ_‰»’Y‘fCO‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB‚ـ‚¸پAˆêژ_‰»’Y‘fCO‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً””M”½‰(ƒ¢Hپƒ0)‚ئ‰¼’肵‚ـ‚·پB‚»‚µ‚ؤپAچ•‰”C(ƒ¢H1=پ|394 kJ/mol)‚ئˆêژ_‰»’Y‘fCO(ƒ¢H2=پ|283 kJ/mol)‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ–â‘蕶‚إ—^‚¦‚ç‚ê‚ؤ‚¢‚é‚ج‚إپAٹ®‘S”Rڈؤگ¶گ¬•¨‚إ‚ ‚é“ٌژ_‰»’Y‘fCO2(ٹ®‘S”Rڈؤگ¶گ¬•¨)‚ًˆê”ش‰؛‚ةڈ‘‚«‚ـ‚·پB

گ}.5 ƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@‚إˆêژ_‰»’Y‘fCO‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹پ‚ك‚é
گ}.3‚جƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚و‚èپAƒ¢Hپپپ|294+283‚ب‚ج‚إپAگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢Hپپپ|111 kJ/mol‚ئ‚¢‚¤‚±‚ئ‚ھ•ھ‚©‚è‚ـ‚·پB
(4) —^‚¦‚ç‚ꂽ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p•û–@
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA(3)‚إژ¦‚µ‚½•û–@‚إ‹پ‚ك‚é‚ج‚ھˆê”ت“I‚إ‚·پB‚µ‚©‚µ‚ب‚ھ‚çپAژہ‚ح‚à‚ء‚ئٹب’P‚ة”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹پ‚ك‚é•û–@‚ھ‚ ‚è‚ـ‚·پB‚½‚¾‚µپA‚±‚ج•û–@‚حپAگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ـ‚½‚ح”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[پAŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج‚¢‚¸‚ê‚©‚ھپA”½‰Œn‚ج‚·‚ׂؤ‚ج•¨ژ؟‚ة‚آ‚¢‚ؤ•ھ‚©‚ء‚ؤ‚¢‚ب‚¢‚ئژg‚¦‚ـ‚¹‚ٌپB‚ـ‚½پA‚±‚ج•û–@‚حپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ً‹@ٹB“I‚ة‹پ‚ك‚é‚à‚ج‚ب‚ج‚إپAڈ‰ٹwژز‚ھ‚±‚ج•û–@‚ة—ٹ‚è‰ك‚¬‚é‚ئپA”M‰»ٹw‚جگ³‚µ‚¢—‰ً‚ھگ¬‚³‚ê‚ب‚¢‚ئ‚¢‚¤‹°‚ê‚à‚ ‚è‚ـ‚·پB‚±‚ج•û–@‚حپAڈء‹ژ–@‚âƒGƒ“ƒ^ƒ‹ƒsپ[گ}–@‚ًڈK“¾‚µ‚½ڈم‚إپAژg‚¤‚±‚ئ‚ً‚¨ٹ©‚ك‚µ‚ـ‚·پB
(i) گ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‰»ٹw•د‰»‚ةٹض—^‚·‚镨ژ؟‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚©‚çپAƒwƒX‚ج–@‘¥‚ً—ک—p‚µ‚ؤ‹پ‚ك‚ç‚ê‚ـ‚·پB—ل‚¦‚خپA‰»ٹw”½‰ژ®aXپ{bYپ¨cZ‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤپAX, Y, Z‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ھٹeپXx, y, z kJ/mol‚إ—^‚¦‚ç‚ê‚é‚ئ‚«پA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚حپAژں‚جƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚إژ¦‚³‚ê‚éٹضŒW‚ھ‚ ‚è‚ـ‚·پBگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‚ ‚鉻چ‡•¨‚ً‚»‚جگ¬•ھŒ³‘f‚ج’P‘ج‚©‚çچى‚é‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ب‚ج‚إپA’P‘ج‚ًƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚جˆê”شڈم‚ةڈ‘‚«‚ـ‚·پB

گ}.6 گ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p
ƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚و‚èپAƒ¢Hپپcz-(axپ{by)‚ئ‚ب‚è‚ـ‚·پB‚±‚±‚إپAcz‚حگ¶گ¬•¨Z‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکaپAaxپ{by‚ح”½‰•¨X‚¨‚و‚رY‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB‚آ‚ـ‚èپA”½‰Œn‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ—^‚¦‚ç‚ê‚ؤ‚¢‚é‚ئ‚«‚حپAژںژ®‚ج‚و‚¤‚ةگ¶گ¬•¨‚ئ”½‰•¨‚ج‚»‚ꂼ‚ê‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚جچ·‚©‚çپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ھ‹پ‚ك‚ç‚ê‚ـ‚·پB
aXپ@پ{پ@bYپ@پ¨پ@cZپ@‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤ
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H پپ (گ¶گ¬•¨Z‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa) - (”½‰•¨X‚¨‚و‚رY‚جگ¶گ¬ƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa)
(ii) ”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‰»ٹw•د‰»‚ةٹض—^‚·‚镨ژ؟‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚©‚çپAƒwƒX‚ج–@‘¥‚ً—ک—p‚µ‚ؤ‹پ‚ك‚ç‚ê‚ـ‚·پB—ل‚¦‚خپA‰»ٹw”½‰ژ®aXپ{bYپ¨cZ‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤپAX, Y, Z‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ھٹeپXx, y, z kJ/mol‚إ—^‚¦‚ç‚ê‚é‚ئ‚«پA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚حپAژں‚جƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚إژ¦‚³‚ê‚éٹضŒW‚ھ‚ ‚è‚ـ‚·پB”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚حپA‚ ‚镨ژ؟‚ًٹ®‘S”Rڈؤ‚³‚¹‚½‚ئ‚«‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ب‚ج‚إپA”Rڈؤگ¶گ¬•¨‚ًƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚جˆê”ش‰؛‚ةڈ‘‚«‚ـ‚·پB

گ}.7 ”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج—ک—p
ƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚و‚èپAƒ¢Hپپ(axپ{by)-cz‚ئ‚ب‚è‚ـ‚·پB‚±‚±‚إپAcz‚حگ¶گ¬•¨Z‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکaپAaxپ{by‚ح”½‰•¨X‚¨‚و‚رY‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB‚آ‚ـ‚èپA”½‰Œn‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ—^‚¦‚ç‚ê‚ؤ‚¢‚é‚ئ‚«‚حپAژںژ®‚ج‚و‚¤‚ةگ¶گ¬•¨‚ئ”½‰•¨‚ج‚»‚ꂼ‚ê‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚جچ·‚©‚çپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ھ‹پ‚ك‚ç‚ê‚ـ‚·پB
aXپ@پ{پ@bYپ@پ¨پ@cZپ@‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤ
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H پپ (”½‰•¨X‚¨‚و‚رY‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa) - (گ¶گ¬•¨Z‚ج”RڈؤƒGƒ“ƒ^ƒ‹ƒsپ[‚ج‘چکa)
(iii) Œ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج—ک—p
‰»ٹw”½‰‚حپAˆê”ت“I‚ةƒGƒlƒ‹ƒMپ[‚جڈo“ü‚è‚ً”؛‚¢‚ـ‚·پB‚»‚ج——R‚حپA‰»ٹw”½‰‚ھ‹N‚±‚é‚ئ‚«پA”½‰•¨’†‚ج‰»ٹwŒ‹چ‡‚ھگط‚ê‚ؤپA—±ژq‚ج‘g‚فٹ·‚¦‚ھ‹N‚±‚èپAگV‚½‚ب‰»ٹwŒ‹چ‡‚ھگ¶‚¶‚ؤپAگ¶گ¬•¨‚ھ‚إ‚«‚é‚©‚ç‚إ‚·پB‚µ‚½‚ھ‚ء‚ؤپA”½‰•¨‚ئگ¶گ¬•¨‚ج‚»‚ꂼ‚ê‚ج‰»ٹwŒ‹چ‡‚جƒGƒlƒ‹ƒMپ[چ·‚ج•ھ‚¾‚¯پAƒGƒlƒ‹ƒMپ[‚ھڈo“ü‚è‚·‚é‚ح‚¸‚إ‚·پB•ھژq“à‚ج‹¤—LŒ‹چ‡‚ًگط’f‚·‚邽‚ك‚ة•K—v‚بƒGƒlƒ‹ƒMپ[‚ًپuŒ‹چ‡ƒGƒlƒ‹ƒMپ[(bond energy)پv‚ئ‚¢‚¢پA‹C‘ج•ھژq“à‚ج1 mol“–‚½‚è‚ج’l‚إژ¦‚µ‚ـ‚·پB—ل‚¦‚خپA1 mol‚جگ…‘f•ھژqH2‚ً2 mol‚جگ…‘fŒ´ژqH‚ة•ھ‰ً‚·‚邽‚ك‚ة‚حپAH-H‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[436 kJ/mol‚ة‘ٹ“–‚·‚éƒGƒlƒ‹ƒMپ[‚ً‰ء‚¦‚é•K—v‚ھ‚ ‚è‚ـ‚·(‹z”M”½‰)پB‚»‚µ‚ؤپA‹t‚ة2 mol‚جگ…‘fŒ´ژqH‚ھ1 mol‚جگ…‘f•ھژqH2‚ة‚ب‚é‚ئ‚«‚ة‚حپAH-H‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ة‘ٹ“–‚·‚éƒGƒlƒ‹ƒMپ[‚ھ”گ¶‚µ‚ـ‚·(””M”½‰)پB
H2(g)پ@پ¨پ@2H(g)پ@پ@پ@ƒ¢H پپپ{436 kJ
2H(g)پ@پ¨پ@H2(g)پ@پ@پ@ƒ¢H پپپ|436 kJ
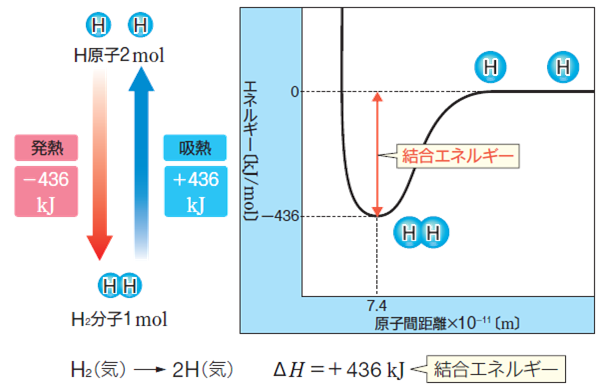
گ}.8 گ…‘f•ھژqH2‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[
‚µ‚½‚ھ‚ء‚ؤپA”½‰•¨‚ئگ¶گ¬•¨‚ج‚»‚ꂼ‚ê‚ج‰»ٹwŒ‹چ‡‚جƒGƒlƒ‹ƒMپ[چ·‚©‚çپAƒwƒX‚ج–@‘¥‚ً—ک—p‚µ‚ؤ”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ھ‹پ‚ـ‚è‚ـ‚·پB—ل‚¦‚خپA‰»ٹw”½‰ژ®A2(‹C)پ{B2(‹C)پ¨2AB(‹C)‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤپAA-A, B-B, A-B‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ھپAٹeپXx, y, z kJ/mol‚إ—^‚¦‚ç‚ê‚é‚ئ‚«پA”½‰Œn‚جƒGƒ“ƒ^ƒ‹ƒsپ[‚حپAژں‚جƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚إژ¦‚³‚ê‚éٹضŒW‚ھ‚ ‚è‚ـ‚·پBŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚حپA‚ ‚é‹C‘ج•ھژq‚ج‹¤—LŒ‹چ‡‚ًگط’f‚µ‚ؤپAƒoƒ‰ƒoƒ‰‚جŒ´ژq‚ة‚·‚é‚ئ‚«‚ة•K—v‚ب”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[‚ب‚ج‚إپAŒ´ژq‚ًƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚جˆê”شڈم‚ةڈ‘‚«‚ـ‚·پB

گ}.9 Œ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج—ک—p
ƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚و‚èپAƒ¢Hپپ(xپ{y)-2z‚ئ‚ب‚è‚ـ‚·پB‚±‚±‚إپA2z‚حگ¶گ¬•¨AB‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج‘چکaپAxپ{y‚ح”½‰•¨A2‚¨‚و‚رB2‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج‘چکa‚ً•\‚µ‚ؤ‚¢‚ـ‚·پB‚آ‚ـ‚èپA”½‰Œn‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ھ—^‚¦‚ç‚ê‚ؤ‚¢‚é‚ئ‚«‚حپAژںژ®‚ج‚و‚¤‚ةگ¶گ¬•¨‚ئ”½‰•¨‚ج‚»‚ꂼ‚ê‚ج‰»ٹwŒ‹چ‡‚جƒGƒlƒ‹ƒMپ[‚جچ·‚©‚çپA”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ھ‹پ‚ك‚ç‚ê‚ـ‚·پB
A2(‹C)پ@پ{پ@B2(‹C)پ@پ¨پ@2AB(‹C) پ@‚ج”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H‚ة‚آ‚¢‚ؤ
”½‰ƒGƒ“ƒ^ƒ‹ƒsپ[ƒ¢H پپ (”½‰•¨A2‚¨‚و‚رB2‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج‘چکa) - (گ¶گ¬•¨AB‚جŒ‹چ‡ƒGƒlƒ‹ƒMپ[‚ج‘چکa)
(5) ƒwƒX‚ج–@‘¥‚ج‰—p
Œإ‘جŒ‹ڈ»‚جڈَ‘ش‚ة‚ ‚é—zƒCƒIƒ“‚ئ‰AƒCƒIƒ“‚ًٹ®‘S‚ةگط‚è—£‚µ‚ؤپA‚خ‚ç‚خ‚ç‚ج‹C‘جڈَ‘ش‚ة‚·‚é‚ج‚ة•K—v‚بƒGƒlƒ‹ƒMپ[‚ج‚±‚ئ‚ًپAپuٹiژqƒGƒlƒ‹ƒMپ[(lattice energy)پv‚ئ‚¢‚¢‚ـ‚·پB—ل‚¦‚خپA‰–‰»ƒiƒgƒٹƒEƒ€NaCl‚جŒ‹ڈ»‚جٹiژqƒGƒlƒ‹ƒMپ[QپkkJ/molپl‚حپAژںژ®‚ج‚و‚¤‚ة•\‚³‚ê‚ـ‚·پB
NaCl(Œإ)پ@پ¨پ@Na+ (‹C)پ@پ{پ@Cl- (‹C) پ@پ@پ@ƒ¢H پپ Q kJ
ٹiژqƒGƒlƒ‹ƒMپ[Q‚حپA’¼گع‘ھ’è‚·‚邱‚ئ‚ھچ¢“ï‚إ‚·پB‚»‚±‚إپAƒwƒX‚ج–@‘¥‚ً—p‚¢‚ؤپAŒvژZ‚ة‚و‚èٹشگع“I‚ة‹پ‚ك‚ـ‚·پB‘هٹw“üژژ‚إ‚حپAژں‚جگ}.10‚ج‚و‚¤‚بƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ًڈ‘‚¢‚ؤپAٹiژqƒGƒlƒ‹ƒMپ[Q‚ً‹پ‚ك‚³‚¹‚é–â‘è‚ھ‚µ‚خ‚µ‚خڈo‘肳‚ê‚ـ‚·پB‚±‚جƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚ً—p‚¢‚ؤپANaCl(Œإ)‚جŒ‹ڈ»1 mol‚ً‹C‘جڈَ‘ش‚جƒiƒgƒٹƒEƒ€ƒCƒIƒ“Na+ (‹C)‚ئ‰–‰»•¨ƒCƒIƒ“Cl- (‹C)‚ةˆّ‚«—£‚·‚ج‚ة•K—v‚بٹiژqƒGƒlƒ‹ƒMپ[Q‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
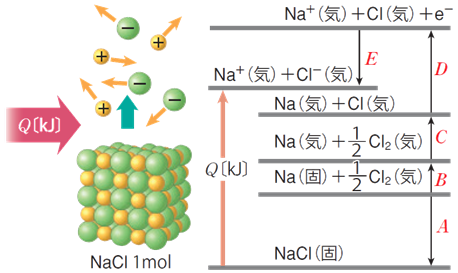
گ}.10 ƒGƒ“ƒ^ƒ‹ƒsپ[گ}‚و‚èپAٹiژqƒGƒlƒ‹ƒMپ[Q‚ً‹پ‚ك‚é

گ}.10‚ج‚و‚¤‚ةپAƒwƒX‚ج–@‘¥‚ً‰—p‚µ‚ؤپAژہŒ±’l‚ةٹî‚أ‚«ƒCƒIƒ“Œ‹ڈ»‚جٹiژqƒGƒlƒ‹ƒMپ[Q‚ً‹پ‚ك‚éڈzٹآ‰ك’ِ‚ج‚±‚ئ‚ًپAپuƒ{ƒ‹ƒ“¥ƒnپ[ƒoپ[ƒTƒCƒNƒ‹(Born-Haber cycle)پv‚ئ‚¢‚¢‚ـ‚·پB‚±‚ê‚و‚èپAٹiژqƒGƒlƒ‹ƒMپ[Q‚حپAژں‚ج‚و‚¤‚ةٹشگع“I‚ة‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
![]()
![]()
پEژQچl•¶Œ£
1) êژ“،—َ/“،“ˆڈ؛/ژR–{—²ˆê/‘¼19–¼پu‰»ٹwپvŒ[—رٹظ(2012”N”چs)
2) گخگىگ³–¾پuگV—Œn‚ج‰»ٹw(‰؛)پvڈx‘ن•¶Œة(2005”N”چs)
3) –m•”‹g—f¢‰»ٹw‚جگVŒ¤‹†£ژOڈب“°(2013”N”چs)
4) “n•سگ³/–kٹ”ژ•F ‹¤’کپuچ‚چZ‚إ‹³‚ي‚肽‚©‚ء‚½‰»ٹwپv“ْ–{•]ک_ژذ(2008”N”چs)