�E�������x�Ɖ��w���t
�y�ڎ��z
(2) �������x���x�z����v���Ɣ������x��
(ii) �����ɖ��W�ȕ����������Ă��A�Z�x�≷�x�����Ȃ�Ε��t�͈ړ����Ȃ�
(ii-3) �G�}�������Ă����t�͈ړ����Ȃ�
(8) ���w���t�ɂ����锽���G���^���s�[
(1) �������x�̒�`
���w�����Ƃ́A�������̌�������A���q�ԂɐV�����������ł��āA����������������̂ł��B���w�����ł́A�����������Ƃ��ɁA������1���Ȃ���Ȃ�Ȃ��̂ŁA�����G�l���M�[�̑傫�����q�Ȃǂ́A���w�������N����ɂ����̂ł��B�܂��A�V�����������ł���ۂɂ��A���q�̍\�������ݍ����Ă���ƁA���̓I�ȏ�Q�ɂ��A���������������ɂ����Ƃ����悤�Ȃ��Ƃ�����܂��B���������āA���w�����Ƃ������̂́A��u�ŏI���悤�Ȃ��̂ł͂Ȃ��A�������ɃG�l���M�[��^���āA����������������肵�Ȃ���Ȃ炸�A������x�̎��Ԃ�������̂ł��B
���w�������ɂ�����1�̕����ɒ��ڂ����Ƃ��A�P�ʎ��Ԃ�����̃����Z�x�̕ω��ʂ��A���̕����́u�������x(reaction velocity)�v�Ƃ����܂��A�������x�́A��ʓI�ɐ�Βl�ŕ\���܂��B�����ʂł͂Ȃ������Z�x���g�����R�́A�������x�͑̐ς̉e�����邩��ł��B�Ⴆ�A���镨��1 mol��������Ƃ��܂��傤�B�傫���e��Ə������e�킪����A���R�������e��̕����������������N����܂��B���������āA�������x�́A�̐ς̉e�����l���������Z�x���g���ĕ\���̂������I�ɂȂ�܂��B�����ŗ�Ƃ��āAA2��B2���������AAB����������Ƃ������w�������l���Ă݂܂��傤�BA2�̃����Z�x[A2]�̎��ԕω����O���t�ɂ���ƁA���̐}.1�̂悤�ɂȂ�܂��B
A2�@�{�@B2�@���@2AB
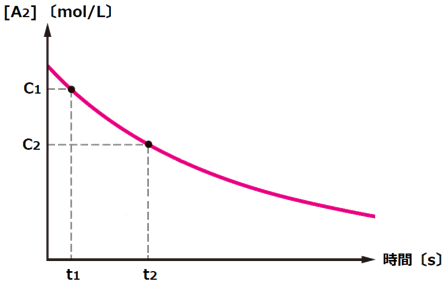
�}.1 [A2]�̎��ԕω�
�}.1�̂悤�ɁA�Z�x�̎��ԕω����A�O���t�ɂ���ĘA���I�ɗ^�����Ă���ꍇ�́A�e���Ԃ̏u�Ԃ̑��x���A�O���t�̌X�����狁�߂邱�Ƃ��ł��܂��B�܂�A�������x�́A�Z�x�̎��Ԕ����ŗ^������̂ł��B�Ⴆ�A����t1�k�b�l�ɂ�����u�Ԃ�A2�̔������x��vA�Ƃ���ƁA���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
![]()
�������A�}.1�̂悤�ɃO���t�����̂�����ȏꍇ�A�Z�x�̎��Ԕ����ɂ���āA�������x�����߂邱�Ƃ��ł��܂���B�Ⴆ�A�Z�x��C1, C2 �������A�̂悤�ɂƂтƂтɂ����^�����Ă��Ȃ��ꍇ�A2�̎���t1�`t2�k�b�l�ɂ����镽�ϑ��x���A�������x�Ƃ��ċ��߂邱�ƂɂȂ�܂��B�����ŁA����t1�`t2�k�b�l�ɂ����镽�ς�A2�̔������x��![]() �Ƃ���ƁA���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
�Ƃ���ƁA���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
![]()
�܂��A���̔����ł́AA2��B2��1���Ȃ��Ȃ�����AAB��2������̂ŁA�Z�x�̕ω��ʂ̊Ԃɂ́A���̂悤�ȊW�����藧���Ă��܂��B
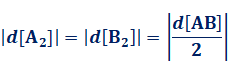
�����ŁA���̔����S�̂̋��ʂ̑��xv�Ƃ��āA���̂悤�ɒ�`���邱�Ƃ������ł��B
![]()
(2) �������x���x�z����v���Ɣ������x��
�@���w������i�s�����邽�߂ɂ́A���w������邾���̃G�l���M�[���K�v�ɂȂ�܂��B�Ⴆ�A���fH2�ƃ��E�fI2���������āA���E�����fHI���������锽���ɂ��čl���Ă݂܂��傤�B
H2�@�{�@I2�@���@2HI�@�{�@9.0 kJ
���̔�����i�s�����邽�߂ɂ́A�܂��͔������̗��q���m���Փ˂��Ȃ���Ȃ�܂���B�������A���������m���Փ˂�������Ƃ����āA�K����������Ƃ͌���܂���B�����̉��w�����ł́A�������N���邽�߂ɂ́A������ȏ�̃G�l���M�[�������āA���w��������₷���u���������(activated state)�v�ɂ��Ȃ���Ȃ�Ȃ��̂ł��B���̉�����ׂ��ŏ��̃G�l���M�[���A��ʓI�Ɂu�������G�l���M�[(activation energy)�v�Ƃ����܂��B�������G�l���M�[�ȏ�̉^���G�l���M�[�������Ȃ����q���m�̏Փ˂ł́A�����͐i�s���Ȃ��̂ł��B
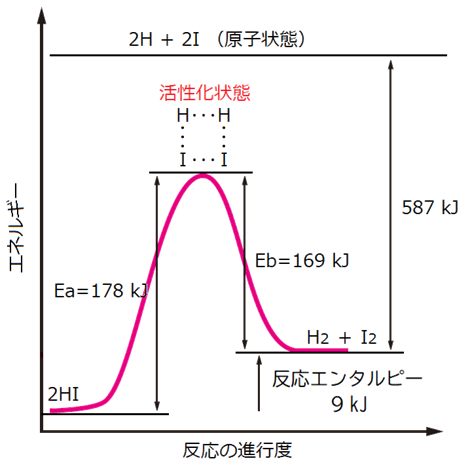
�}.2 �����o�H�ƃG�l���M�[���
���������āA�������Ɋ������G�l���M�[�ȏ�̃G�l���M�[��^���A�������x��傫�����邽�߂ɂ́A��ʓI�Ɏ��̂悤�ȍH�v���K�v�ƂȂ�܂��B
(i) �������̔Z�x��傫������
���w������i�s�����邽�߂ɂ́A���������m�̏Փ˂��K�v�s���ł��B��ʓI�ɒP�ʎ��ԓ�����ɏՓ˂��闱�q�̐��������قǁA�������x�͑傫���Ȃ�܂��B���q���ړ����₷���C�̂�n�t���̔����ł́A�������̔Z�x��傫������ƁA���������m���Փ˂���m�����傫���Ȃ�̂ŁA�������x�͑傫���Ȃ�܂��B
����ŁA�ő̂��W���锽���ł́A�ő̂��ׂ������Ă����ƁA�������x�͑傫���Ȃ�܂��B����́A�����ʂł́A����蕲����̕����A�\�ʐς��������傫���āA�݂��ɐڐG�ł��闱�q�̐����A�ɂ߂đ傫���Ȃ邽�߂ł��B�Ⴆ�A�SFe�͉��ł́A��C���ł̔��������Ⴂ�̂ł����A���ׂȕ�����ɂ���ƁA��C�ƐG�ꂽ�����Ŕ�����悤�ɂȂ�܂��B���̂��߁A���h�@�ɂ���āA���ʈȏ�̓S���͊댯�������ƂȂ��Ă��܂��B
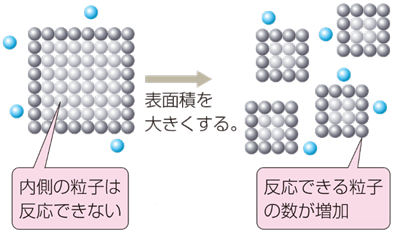
�}.3 �\�ʐςɂ�锽�����x�̈Ⴂ
(ii) ���x���グ��
���x���グ��ƁA�����^���G�l���M�[�����������q�̊������������܂��B���̂��߁A���������m���Փ˂����Ƃ��ɁA�������G�l���M�[�ȏ�̉^���G�l���M�[�����������q�̊������������܂��B���x�������Ȃ�ƁA�{���c�}�����z�ɂ����銈�����G�l���M�[�ȏ�̃G�l���M�[�������q�����A�}���ɑ�������̂ł��B�����̉��w�����ŁA�����t�߂ł́A���x��10 K�オ�邲�ƂɁA�������x�͂��悻2�`3�{�ɂȂ�܂��B
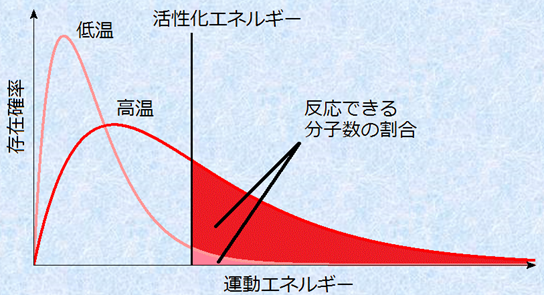
�}.4 ���x�������Ȃ�ƁA�������G�l���M�[�ȏ�̃G�l���M�[�������q�����}���ɑ�������
(iii) �G�}��������
�����̑O��ł��ꎩ�g�͕ω����Ȃ����̂́A�������x��傫������悤�ȕ������A��ʓI�Ɂu�G�}(catalyst)�v�Ƃ����܂��B�G�}�́A���w�H�Ƃɂ����Ĕ��ɏd�v�ł���A���݂̉��w�H�Ƃ̃v���Z�X��80%�ȏオ�A�G�}��p���đ��Ƃ���Ă��܂��B��R�X�g�ŗǎ��ȐG�}���J���E�������邱�Ƃ��A������d�v�ɂȂ��Ă��܂��B
�G�}�́A�������Ƃ̊ԂŁA�������ԑ̂����܂��B�����āA�������ԑ̂��琶�������ł���ƂƂ��ɁA�G�}���Đ�����܂��B�G�}��������ƁA�����̎d�g�݂��ς���āA�������G�l���M�[���������Ȃ邽�߁A�������G�l���M�[�ȏ�̉^���G�l���M�[�������q�̊������������܂��B�G�}�́A�V���Ȋ�������Ԃ�����āA�������G�l���M�[�����������A�������x��傫��������ʂ�����̂ł��B�������A�G�}�͊������G�l���M�[�����������܂����A�����G���^���s�[�͕ω������܂���B�܂��A�G�}�͋t�����̊������G�l���M�[������������̂ŁA�t�����̔������x���傫���Ȃ�܂��B
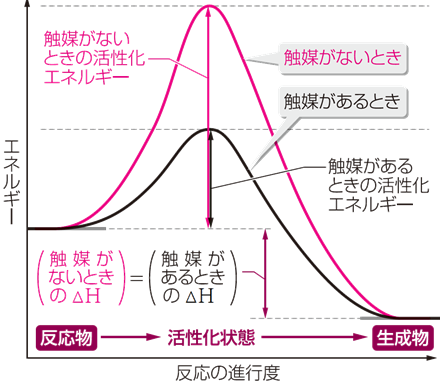
�}.5 �G�}�͊������G�l���M�[������������
�@�ȏ�̂��Ƃ��A�������xv�́A���̂悤�Ȏ��ɂȂ邱�Ƃ��z��ł��܂��BA2�{B2��2AB�̔����ɂ����āA
![]()
���̂悤�Ȏ����u�������x��(reaction rate equation)�v�Ƃ����Ak���u�������x�萔(reaction rate constant)�v�A���{�����u��������(order of reaction)�v�Ƃ����܂��B���̔����ł́AA2��B2��1�F1�̊����Ŕ������邽�߁A��������1�Ŕ���������2�ɂȂ邱�Ƃ��\�z����܂��B�������A����͕K�������W���ʂ�ɂȂ�Ƃ͌��炸�A�����̏ꍇ�͎����ɂ���Č��肳��܂��B���̗��R�́A���ۂ̔����ł́A�������̗��q���������̌W���̐����������ɏՓ˂��āA��i�K�Ŕ�������Ƃ͌���Ȃ�����ł��B���ۂ̔����@�\�́A�\�z�������G�ł���ꍇ�������A�������̔������g�ݍ��킳���Đi�ޏꍇ������̂ł��B���̂悤�ȏꍇ�́A�������x���P���ɔ������̔Z�x�ɔ�Ⴗ��Ƃ͌���܂���B�܂��A��i�K�ŋN���锽���ł��A�������x�͍ł��x�������i�K�Ɉˑ����āA��i�K�̂悤�Ɉ�����Ƃ�������܂��B
(3) �A���j�E�X�̎�
�������xv�́A���x�⊈�����G�l���M�[�ɂ��x�z�����̂ł����A�������x�����̔Z�x�̕���([A2]��[B2]��)�ɂ́A�����̈��q���S���܂܂�Ă��܂���B���������āA���x�⊈�����G�l���M�[�́A�������x�萔k�̒��Ɋ܂܂�邱�ƂɂȂ�܂��B�A�������x�萔k�̒l�́A�����◝�_���A���́u�A���j�E�X�̎�(Arrhenius equation)�v�ŗ^�����܂��B
![]()
�����ŁAR�͋C�̒萔�AEa�͊������G�l���M�[�AT �͌n�̉��x�AC�͕p�x���q�̒萔�ł��B�A���j�E�X�̎��ł́A���̕��G������A�����x�萔k�����܂ЂƂC���[�W�����ɂ����ł����A�A���j�E�X�̎��ɂ����āA���xT �̋Ɍ�������Ă݂�ƁA���̂悤�ȊȌ��ȊW�ɂȂ�܂��B
![]()
![]()
�����̎����番���邱�Ƃ́A���xT ���傫���قǁA�������x�萔k���傫���Ȃ�A�������xv����������Ƃ������Ƃł��B�A���j�E�X�̎��ɂ����āA�Ɨ��ϐ�������e-Ea/RT ���u�{���c�}�����q(Boltzmann factor)�v�Ƃ����A���xT �Ŋ������G�l���M�[Ea���傫�ȉ^���G�l���M�[�������q�̊���(�m��)��\���܂��B�܂�A�A���j�E�X�̎��́A���x���グ��Ɗ������G�l���M�[���傫�ȉ^���G�l���M�[�������q�̊�����������Ƃ������Ƃ��A�@���ɕ\�������Ȃ̂ł��B�Ⴆ�A�������G�l���M�[��Ea��0�Ȃ�A���xT�ɊW�Ȃ�e0��1�ƂȂ�̂ŁA���ׂĂ̕��q���������G�l���M�[������^���G�l���M�[�������ƂɂȂ�܂��B�������G�l���M�[��Ea��0�̔����́A���q���m���Փ˂���ΕK���������g�ݑւ�锽�����Ӗ����A���R�E�ōł����������ƂȂ�܂��B���}�ȗ�Ƃ��āA�_�Ɖ���̒��a�����́A�������G�l���M�[Ea���ق�0���ƕ������Ă��܂��B
�܂��A�A���j�E�X�̎����O���t�ɂ���ꍇ�A�����ɉ��xT�����ƁA�������x�萔k�͂����ɔ��U���Ă��܂��܂��B�����ŁA�A���j�E�X�̎��̗��ӂ̎��R�ΐ������ƁA���̂悤�Ɉꎟ��y��ax�{b�̌`�ɕό`�ł��܂��B���̂悤�ɗ��ӂ̑ΐ�����邱�ƂŁA���G�Ȋ����ꎟ���ɂ��邱�Ƃ��ł���̂ł��B
![]()
![]()
�����āA�c����lnk�A������1/T�����A�O���t�������ƁA���̐}.6�̂悤�ɂȂ�܂��B���̂悤�ɂ��ăO���t���쐬���邱�Ƃ��A�u�A���j�E�X�v���b�g(Arrhenius plot)�v�Ƃ����܂��B�������x�萔k�Ɖ��xT�́A�����ɂ�葪��\�Ȓl�Ȃ̂ŁA���̃O���t���A�X�������߂邱�Ƃ��ł��܂��B�����āA���̃O���t�̌X�����A�������G�l���M�[Ea�������I�ɋ��߂邱�Ƃ��ł��܂��B
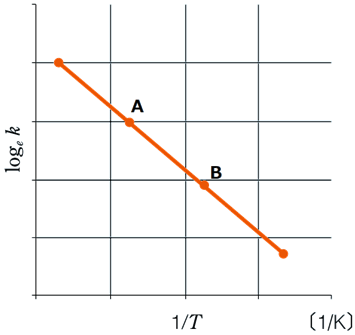
�}.6 �A���j�E�X�v���b�g
![]()
![]()
(4) �M�u�X�̎��R�G�l���M�[
���w���������R�ɐi�s���邩�ǂ������A��ʓI�ɔ��f������@�͂Ȃ��̂ł��傤���H���̕��@�����o�����̂́A�A�����J�̕������w�҃E�B���[�h�E�M�u�X�ł��B���w�������ʓI�ɕ��͂ł��鎮�Ƃ��āA�u�M�u�X�̎��R�G�l���M�[(Gibbs' free energy)�v�Ƃ�����������܂��B�M�u�X�̎��R�G�l���M�[�ω���G�́A��ʓI�Ɏ��̂悤�ɕ\�����Ƃ��ł��܂��B�Ȃ��A�L����(�f���^)�͉p��́udifference(��)�v�̓������̃M���V�A�����ŁA�ω��ʂ�\���܂��B
![]()
�����ŁAG���u���R�G�l���M�[(free energy)�v�AH���u�G���^���s�[(enthalpy)�v�AS���u�G���g���s�[(entropy)�v�Ƃ����܂��B�u�M�͊w���@��(second law of thermodynamics)�v���A�n�͎��R�G�l���M�[G�����������ɐi�s���܂��B�܂�A���̎��ɂ����āA���R�G�l���M�[�ω���G����G��0�ł���Ȃ�A���̔����͎��R�ɐi�ޔ����ł���A��G����G��0�ł���Ȃ�A���̔����͎��R�ɂ͐i�܂Ȃ������ɂȂ�܂��B�܂��A�G���^���s�[H�́A�n�̃G�l���M�[�ɊW������q�ł���A�G���g���s�[S�́A�n�̗��G��(�U���)�ɊW������q�ł��B�܂�A���w�������i�s���邩�ǂ����́A�n�́u�G�l���M�[�ω��v�Ɓu���G���̕ω��v�ɂ���Č��܂�̂ł��B
(i) �����G�l���M�[
�@�����̍\�����q�́A�M�^���ɂ��^���G�l���M�[�������Ă��܂��B�܂��A�����̗��q�́A�݂��ɗ͂��y�ڂ������A���q�Ԃ̗͂ɂ��ʒu�G�l���M�[�������Ă��܂��B�����̃G�l���M�[�̑��a���A�����́u�����G�l���M�[(internal energy)�v�Ƃ����܂��B�����G�l���M�[�̓G�l���M�[�̎����������A�L��U�ŕ\����܂��B�����G�l���M�[U�́A���̈��͂�̐ςɊW�Ȃ��A�����ʂƉ��x�����Ō��܂�܂��B�����̉��xT�������قǁA���q�̔M�^���͌������Ȃ�A�����G�l���M�[U�͑傫���Ȃ�܂��B
�@�����̓����G�l���M�[U�́A�O�������������MQ��O�����炳���d��W�ɂ���ĕω����܂��B���̂Ƃ��A�n�ɉ�����ꂽ�M��Q�ƊO�����炳�ꂽ�d��W�̘a�́A�n�̓����G�l���M�[�ω���U�Ɠ������Ȃ�܂��B������u�M�͊w���@��(first law of thermodynamics)�v�Ƃ����A���̖@���́u�G�l���M�[�̕ۑ��v��\���@����1�ł��B�Ȃ��A�M�Ǝd���̌����ɂ��āA���̌������ǂ���Ƃ��邩�͕����ɂ���ėl�X�ł��B�����ł́A�M�Ǝd���̌������A�u�O��(�O�E)����n�Ɍ����������v�𐳂Ƃ��Ă��܂��B
![]()
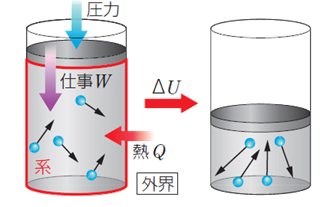
�}.7 �����G�l���M�[�ƔM�͊w���@��
�Ȃ��A�n�̑̐ς����ɂ������(���ωߒ�)�ł́A�O�����炳���d��W��0�ɂȂ�܂��B���̂悤�ȓ��ωߒ��ł́A�O�������M��������ƁA���̂��ׂĂ������G�l���M�[�̏㏸�Ɏg���邱�ƂɂȂ�܂��B�܂�A�̐ψ��̏����Ȃ�A�����G�l���M�[�ω���U�́A�n�ɉ�����ꂽ�MQ���̂��̂ɂȂ�܂��B
![]()
�������A���w�������l����ۂɂ́A���ωߒ�������������(���͂����ɂ������)�̕��������ł��B���͈��̏����ŔM��\�������Ƃ��ɗp����̂��A�����́u�G���^���s�[�v�Ȃ̂ł��B
(ii) �G���^���s�[
�@�u�G���^���s�[(enthalpy)�v�Ƃ́A�����̔��M��z�M�̋����Ɋւ���ԗʂ����B�M���V�A��́u���܂�(enthalpein)�v�ɗR�����Ă���A�u�M�ܗ�(heat content)�v�Ƃ������܂��B�n�ɊO��(�O�E)����M��������ƁA�n�̓����G�l���M�[�͑��債�܂����A������ꂽ�M�̈ꕔ�́A�C�̖̂c���̎d���Ɏg���Ă��܂��܂��B���̖c���Ɏg��ꂽ�d���̃G�l���M�[������G�l���M�[�ɉ��������̂��A�G���^���s�[�ł��B�G���^���s�[H�̓G�l���M�[�̎����������A�����G�l���M�[��U�A���͂�P�A�̐ς�V�Ƃ���ƁA�G���^���s�[H�͎��̂悤�ɒ�`����܂��B
![]()
�@���w�����́A��C�����Ȃǂ̂悤�Ɉ��͂����ɂ������(�����ߒ�)�ōl���邱�Ƃ������ł��B�����ŁA����P��萔�ƌ��Ȃ��āA�����O��̃G���^���s�[�ω���H���l����ƁA���̂悤�ɂȂ�܂��B
![]()
�@�����ŁA�n�ɉ�����ꂽ�M��Q�A�n�ɉ�����ꂽ�d����W�Ƃ���ƁA�����G�l���M�[������U����U��Q�{W�̂悤�ɕ\����܂��B�܂��A�����ߒ��ł�P��V�́u�O�E�ɂ����d���v�̂��ƂȂ̂ŁAP��V��-W�̊W���������܂�(������ꂽ�d��W�̌����Ƌt)�B������A��L���G���^���s�[�ω���H�̎�(��H����U�{P��V)����U��Q�{W��P��V��-W��������ƁA�����������ł́A�n�ɏo���肷��MQ�́A�G���^���s�[�ω���H�ɓ������Ȃ邱�Ƃ�������܂��B
![]()
![]()
�@�܂�A���͈��̏����Ȃ�A�G���^���s�[�ω���H�́A�n�ɉ�����ꂽ�MQ���̂��̂Ȃ̂ł��B�����������ɂ���n�����M���ĊO�E�ɔM���o���ƃG���^���s�[�͉�����A�z�M���ĊO�E���M�����ƃG���^���s�[�͏オ��܂��B��Ƃ��āA�������fHCl�Ɛ��_���i�g���E��NaOH�̒��a�������l���Ă݂܂��傤�B
HCl�@�{�@NaOH�@���@NaCl�@�{�@H2O
���̒��a�����͔��M�����ł���A�����̉ߒ��ŊO�E�ɃG�l���M�[��57 kJ/mol�������o���܂��B�܂�A���͈��̏����Ȃ�A���M���ĊO�E�ɔM����o������(57 kJ/mol)�����A�����n�̃G���^���s�[H�́A�����n�̃G���^���s�[H��菬�����Ȃ�͂��ł��B���������āA�����n�̃G���^���s�[H�́A�����n�̃G���^���s�[H�����������Ȃ�܂��B�G���^���s�[�ω���H�Ƃ́A�����n�Ɛ����n�̃G���^���s�[���Ȃ̂ŁA���̒��a��������H�����ŕ\���ƁA���̂悤�ɂȂ�܂��B
��H �� (�����n�̃G���^���s�[H ) - (�����n�̃G���^���s�[H )
�� ��H �� (NaCl��H2O�̃G���^���s�[H ) - (HCl��NaOH�̃G���^���s�[H )
������A���̒��a�����̃G���^���s�[�ω���H�����߂�ƁA��H��-57 kJ�ɂȂ�܂��B�܂�A�G���^���s�[�ω���H�́A��H��0�Ȃ甭�M�����ł���A��H��0�Ȃ�z�M�����Ȃ̂ł��B�G���^���s�[�ω���H�́A�����M�Ɠ������l�ɂȂ�܂����A�����������M�Ƃ͋t�ɂȂ�̂Œ��ӂ��K�v�ł��B���͈��̏���(�J�����ꂽ���w�����n)�Ȃ�A�����M�̐������t�ɂ������l���A���̔����̃G���^���s�[�ω���H�ɂȂ�܂��B
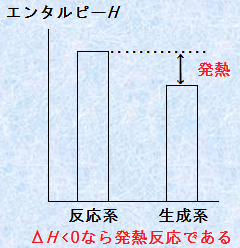
�}.8 �G���^���s�[�ω���H�́A�n�ɏo���肷��MQ�Ɠ�����
(iii) �G���g���s�[
�u�G���g���s�[(entropy)�v�Ƃ́A�n�̗��G���̎w�W�ƂȂ��Ԋ��̂��Ƃł��B�G���g���s�[S�́A�G�l���M�[�����x�Ŋ����������������ASI�P�ʌn�ł�J/K�̎����ł��B���xT�̌n�ɔ����̔M��Q���t�I�ɉ������Ƃ��̃G���g���s�[�ω���S�́A���̂悤�ɕ\����܂��B���̎����Ӗ����邱�Ƃ́A�G���g���s�[�ω���S�́A������ꂽ�M��Q���傫���A�����̌n�̉��xT���Ⴂ�قǁA�G���g���s�[�̑����ɗ^����e�����傫���Ȃ�Ƃ������Ƃł��B
![]()
�Ǘ��n�ɂ����āA�����I�ɋN���鎩�R�ω��́A�K���G���g���s�[S�̑��傷������ɐi�s���Ă����܂��B���̂��Ƃ́A�M�͊w���@���ł��A�u�t�����ł̓G���g���s�[S�͈��ł���A�s���t����(�����I�ω�)�ł̓G���g���s�[S�͑�������v�ƕ\������Ă��܂��B�Ǘ��n�̃G���g���s�[�ω�����S�S�A�n�̃G���g���s�[�ω�����S�n�A�O�E�̃G���g���s�[�ω�����S�O�Ƃ���ƁA�����I�ɋN���锽���ł́A���̊W�����藧���܂��B�Ȃ��A�Ǘ��n�̃G���g���s�[�ω�����S�S��0�̂Ƃ��́A�ω��͉t�I�ŁA�ǂ���̕����ɂ��i�ނ��Ƃ��ł��܂��B
![]()
�܂��A�n�̗��G���́A��ʓI�Ɂu�z�u�̑��l���v�Ɓu�s���̃G�l���M�[�v�̐ςŕ\�����Ƃ��ł��܂��B���G���Ƃ́A���t�̃C���[�W�ʂ�A�������\�����Ă�������q���A�o���o���ɎU����Ă����Ԃ̂��Ƃł��B�����q��������Ɛ������ڂ��Ă������A�o���o���ɎU�������Ԃɂ��Ă��������A�G�l���M�[�I�Ɉ���Ȃ̂ł��B���̗��G����\�����ɂ����āA�G���g���s�[S�́A�z�u�̑��l����\���Ă��܂��B
���G����(�z�u�̑��l��)�~(�s���̃G�l���M�[)
���G���́A�G���g���s�[S�̑傫���ɔ�Ⴗ��̂ŁA�G���g���s�[S���傫��(�����q�̔z�u�̎d�������l�ɂȂ�)�قǁA���G���͑傫���Ȃ�܂��B�܂��A�����q�̍s���̃G�l���M�[���傫���قǁA�����q�̔z�u�����X�ƕς��Ă������Ƃ��ł���̂ŁA���G���͑傫���Ȃ�܂��B�܂�A���q�̔M�^�����������Ȃ鍂���̕����A���G���͑傫���Ȃ�܂��B���ɗ��G�����������锽��(��S��0)�̗�������܂��B
|
�@ ���q�����������锽���@�@2N2O5�@���@4NO2�@�{�@O2 �A ����Ԃ̑�����Ԃւ̕ω��@�@H2O(�t��)�@���@H2O(�C��) �B �^���̎��R�x�̑�����Ԃւ̕ω��@�@H2O(�ő�)�@���@H2O(�t��) �C �g�ݍ��킹�̑��l�ȕ��q�ւ̕ω��@�@(H-H, I-I)�@���@(H-I, H-I) �D ��荬��������Ԃւ̕ω��@�@���@�{�@�G�^�m�[���@���@������ |
(iv) ���R�G�l���M�[
�@���������ߒ��ŁA����Ǘ��n(�n�̎���ɊO�E������)�̉��w�ω����l���Ă݂܂��B�M�͊w���@���ɂ��ƁA�Ǘ��n�ŋN���鎩���I�����́A�K���G���g���s�[S�����傷������ɐi�݂܂��B���̂��߁A�Ǘ��n�̃G���g���s�[�ω�����S�S�A�n�̃G���g���s�[�ω�����S�A�O�E�̃G���g���s�[�ω�����S�O�Ƃ���ƁA�����I�ɋN���锽���ł́A���̊W�����藧���܂��B
![]()
�@�M�͊w���@���ŗ���������̂́A�O�E�̃G���g���s�[�ω���S�O�ł��B�O�E�̃G���g���s�[�ω���S�O�́A���̂Ƃ��̔������x��ړ������M�ʂɂ���ĕω����邩��ł��B�����ŁA�����I�ȕω��̌����̔��ʂ��s���ۂɁA�O�E�̂��Ƃ��l�����ɍς݁A�n�ɂ��Ă����l����悢�悤�ɓ������ꂽ�̂��A�u�M�u�X�̎��R�G�l���M�[(Gibbs' free energy)�v�ł��B�M�u�X�̎��R�G�l���M�[�́A���̂悤���M�͊w���@���̎��������o���邱�Ƃ��ł��܂��B
�@���x�ƈ��͂����ɕۂ����n�ŁA�����I�ɔ������N����A�O�E�ɔM�����o���ꂽ�Ƃ��܂��B���Ƃ̂��A�O�E�̃G���g���s�[�ω���S�O�́A�O�E����n�Ɉړ�����M��Q�A�n�̉��x��T�Ƃ���ƁA��S�O��-Q /T���悤�ɕ\����܂��B�Ȃ��A���̎��ŕ��������ɂȂ闝�R�́A�O�E����n�ɔM���ړ���������𐳂Ƃ������߂ł��B�܂��A�M�͊w���@�����A��U��Q�{W�̊W�����藧�̂ŁAQ����U-W����S�O��-Q /T�ɑ������ƁA���̂悤�ɂȂ�܂��B
![]()
�@�܂��A�����������ł́AP��V�́u�O�E�ɂ����d���v�̂��ƂȂ̂ŁA�n�ɉ�����ꂽ�d��W�́AW��-P��V�ƕ\����܂�(�O�E�ɂ����d���̌����Ƌt�ɂȂ�܂�)�B����āA�Ǘ��n�̃G���g���s�[�ω���S�S�́A���̂悤�ɕό`�ł��܂��B
![]()
![]()
![]()
![]()
�㎮��U�{PV-TS�̕������u�M�u�X�̎��R�G�l���M�[�v�Ƃ����A�L��G�ŕ\���܂��B������A���������ߒ��ł́A�����I�ω�����G��0�ƂȂ邱�Ƃ�������܂��B�܂��A�G���^���s�[H�́AH��U�{PV�ŕ\�����̂ŁA�M�u�X�̎��R�G�l���M�[�ω��́A��G����H-T��S�̂悤�ɕ\���܂��B���̎��ɂ����āA�G���g���s�[�ω���S�Ɖ��xT���ςɂȂ��Ă���̂́A���G�������xT�ɔ�Ⴗ�邩��ł��B���x���オ��ƁA�����q�̍s���̃G�l���M�[���傫���Ȃ�̂ŁA���G�����傫���Ȃ�̂ł��B
![]()
![]()
���w�������i�s���邩�ǂ����́A���R�G�l���M�[�ω���G�̒l�ɂ������Ă��܂��B��G��0�Ȃ�Ή��w�����͐i�s���A��G��0�Ȃ�Ή��w�����͐i�s���܂���B���������ꂾ���Ȃ̂ł����A��G�ɂ�����Ɨ��ϐ��́A��H�E��S�ET��3�����邽�߁A�����̒l���ׂĂ��������Ă��Ȃ���A��G�̐��m�Ȓl�����߂邱�Ƃ��ł��܂���B�������Ȃ���A���鉻�w���������M�I�ɋN����(��H��0)�A�G���g���s�[�ω�����S��0�ł��邱�Ƃ��������Ă���Ȃ�A���R�G�l���M�[�ω��͕K�R�I����G��0�ƂȂ�A���Ȃ��Ƃ����̔����͉��xT�ɂ�炸�A���R�ɐi�s���邱�Ƃ�������܂�(��H����S�̕����͔����̎�ނɂ��܂����AT�̕����͕K�����ɂȂ邩��ł�)�B���̂悤����H�E��S�ET�̒l�����m�ɕ������Ă��Ȃ��Ă��A�������i�s���邩�ǂ����f����p�͂���̂ł��B���̕\.1�ɁA���w���������R�ɐi�s���邩�ǂ����́A�萫�I�Ȕ��f��^����\�������܂��B
�\.1 ���w���������R�ɐi�s���邩�ǂ���
|
�G���^���s�[ |
�G���g���s�[ |
���R�G�l���M�[ |
���� |
|
���M���� �i��H��0�j |
��S��0 |
��G��0 |
���R�ɐi�s���� |
|
��S��0 |
�ቷ����G��0 |
���R�ɐi�s���� |
|
|
��������G��0 |
���R�ɐi�s���Ȃ� |
||
|
�z�M���� �i��H��0�j |
��S��0 |
�ቷ����G��0 |
���R�ɐi�s���Ȃ� |
|
��������G��0 |
���R�ɐi�s���� |
||
|
��S��0 |
��G��0 |
���R�ɐi�s���Ȃ� |
���w���������R�ɐi�s���邩�ǂ����́A���̔��������M�������ǂ����A���邢�͗��G�����������锽�����ǂ����́A2�̗v���ɂ���Č��肳��܂��B���锽�������R�ɐi�s����Ƃ��́A�i�s���邱�Ƃɂ���Čn�̃G�l���M�[���������邩�A���邢�͗��G�����������邩�A���Ȃ��Ƃ��ǂ��炩��������藧���Ă��Ȃ���Ȃ�܂���B���̂ǂ��炩������ۏ���Ȃ���A���������R�ɐi�s���邱�Ƃ͂��肦�Ȃ��̂ł��B
(5) ���w���t
���fH2�ƃ��E�fI2�̍����C�̂��A�f�M���e��ɓ���č����ɕۂƁA���q�Ԃ̌������Փ˂��N����A�ꕔ���������āA���E�����fHI���������Ă��܂��B���̂Ƃ��̐��fH2�̏��ő��x��v1�Ƃ���ƁA���̂悤�ɕ\�����Ƃ��ł��܂��B
H2�@�{�@I2�@���@2HI
![]()
����āA���ő��xv1�́A[H2]��[I2]�ɔ�Ⴗ��̂ŁA�����ƂƂ��ɐ��fH2�����Ȃ��Ȃ�ƁA���ő��xv1�͏������Ȃ��Ă����܂��B����ŁA�������郈�E�����fHI���A�Փ˂�ʂ��Đ��fH2�ƃ��E�fI2�ɕω����Ă����A���fH2�̐������x��v2�Ƃ���ƁA���̂悤�ɕ\�����Ƃ��ł��܂��B
2HI�@���@H2�@�{�@I2
![]()
���̐������xv2�́A[HI]2�ɔ�Ⴗ��̂ŁA�����ƂƂ���[HI]�������Ȃ�ƁA�������xv2�͑傫���Ȃ��Ă����܂��B���������āA������i�߂Ă����ƁA������v1��v2�̏�ԂɂȂ��āA���fH2�̏��ő��x�Ɛ��fH2�̐������x���������Ȃ�u�Ԃ��K��܂��B���̂Ƃ��ɂ́A���fH2�̏��łƐ����������ɋN�����Ă��Ȃ���A���fH2�̗ʂ͈��ɂȂ邽�߁A�u��������ɂ͔������~�܂����悤�ȏ�ԁv�ɂȂ�̂ł��B���̂悤�ȏ�Ԃ��A�u���w���t(chemical equilibrium)�v�Ƃ����܂��B�Ȃ��A�u���t�v�̌ꌹ�́A���e����́uequi(������)�v�Ɓulibra(�o�����X)�v�ɂ��܂��B�Ñネ�[�}�ł́A�d�ʂ�\���upound�v�̂��Ƃ��ulibra�v�ƌĂ�ł��āA���ꂪ�]���āu�o�����X�v�̈Ӗ��ɂȂ�܂����B�܂��A���̂悤�ɂǂ���̕����ɂ��i�ޔ������u�t����(reversible reaction)�v�Ƃ����A�E�����̔������u������(forward reaction)�v�A�������̔������u�t����(reverse reaction)�v�Ƃ����܂��B
���̐}.9�ɁA���fH2�ƃ��E�fI2�̍����C�̂ɂ��āA�������Ƌt�����̔������x�̎��ԕω��������܂����B���̔����ŁAv1��v2�̂Ƃ��́A�����S�̂Ƃ��Đ������̌����ɐi�݁A���̔������x��v1-v2�ƂȂ��āA���E�����fHI���������܂��B�t��v1��v2�̂Ƃ��́A�����S�̂Ƃ��ċt�����̌����ɐi�݁A���̔������x��v2-v1�ƂȂ��āA���E�����fHI���������܂��B
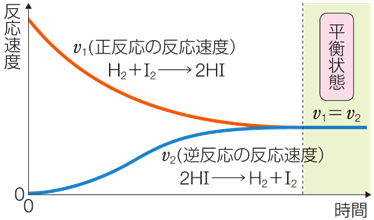
�}.9 �������x�Ɖ��w���t
�@��ʓI�ɁA���Ɏ����悤�Ȕ��������w���t�ɂ���Ƃ��A���t���̊e�����̔Z�x�̊Ԃɂ́A���̂悤�Ȓ萔K�Œ�`�ł��鎮�����藧���܂��B����K�̒l�́A�����̎�ނ≷�x�ɂ���ĈقȂ�܂����A1�̉��w�����ł́A���x�����Ȃ�AK�͈��̒l�ɂȂ�܂��B
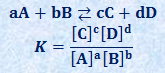
����K���u���t�萔(equilibrium constant)�v�Ƃ����A���̎��ŕ\�����W���A�u���w���t�̖@��(equilibrium law)�v�܂��́u���ʍ�p�̖@��(law of mass action)�v�Ƃ����܂��B��ʂɌő̂�n�}�́A�Z�x�Ȃǂ��l�����A���t�萔K�̎��ɂ͏����܂���B���̎��́A�����ɂ͔M�͊w�̗��_���瓱����܂����A���Ɂu�������x���̔Z�x�̍��̎��������ׂĉ��w�������̌W���Ɉ�v����Ƃ��v�ɂ́A���̂悤�ɏؖ����邱�Ƃ��ł��܂��B

����āA���t�萔K��K��k1/k2�ƂȂ�A���x�����Ȃ�AK�͈��l�ƂȂ�܂��B���fH2�ƃ��E�fI2���烈�E�����fHI���������锽���́A���̂悤�ɔ������x�����牻�w���t�̖@�����o�����Ƃ��ł���̂ŁA��w�����Ȃǂł͕p�ɂɏo�肳��܂��B�������A����͂��Ȃ����ȗ�ł���A���̔����ȊO�ɁA���w�������̌W�����������x���ɔ��f������͂قƂ�ǂ���܂���B��{�I�ɂ́A�������x���ƕ��t�萔�͕ʕ��ƍl���������ǂ��ł��傤�B
�Ȃ��A�M�͊w�̗��_���牻�w���t�̖@�����ɂ́A������Q�Ɗ������̊T�O������K�v������܂��B������Ƃ́A�t�����Ɋւ��锽���̐i��̎ړx�̂��Ƃł��B�܂��A���ʂƂ́A�����Z�x�ɋ߂���������������(�M�͊w�I�Z�x)�ŁA��ʂɂ͉��x�A���́A�����ʂɂ��Ă̕��G�Ȋ��ɂȂ�܂��B�n�t�̏ꍇ�ł́A���ʂ̓����Z�x(mol/L)�ŋߎ����邱�Ƃ��ł��܂��B�M�͊w�̗��_���番����悤�ɁA���t�萔K�̎��Ɍő̂�n�}�������Ȃ��̂́A�����̊��ʂ�����1�Ƃ��Ă��邽�߂ł��B
�\.2 �������ɂ���
|
�n�t�̏ꍇ |
�����Z�x(mol/L)�ŋߎ����� |
|
�����C�̂̏ꍇ |
����������(Pa)�ŋߎ����� |
|
�n�}�̏ꍇ |
����1�Ƃ��� |
|
�ő̂̏ꍇ |
�����Ȍő̂Ȃ�����1�Ƃ��� |
���w���t���������Ă���Ƃ��́A������Q�̒l�́A���t�萔K�̒l���������Ȃ�̂ŁA���̂悤�ɉ��w���t�̖@�����o�����Ƃ��ł��܂��B

�܂��A���t�萔K�́A�M�u�X�̎��R�G�l���M�[�ω���G�Ƃ̊ԂɎ��̂悤�ȊW������܂��B�����ŁAR�͋C�̒萔�Aln�͎��R�ΐ��������܂��B���̎��ɂ���āA���t�萔K�̒l��������A�M�u�X�̎��R�G�l���M�[�ω���G�����߂邱�Ƃ��ł��܂��B
![]()
���w���t�ɂ����āA�������̕����L���Ȕ����ł�K��1�Ȃ̂ŁA���̎��ł���G��0�ƂȂ�A���������R�ɐi�ނ��Ƃ�\���܂��B�܂��A���̎������̂悤�ɏ��������ƁA�A���j�E�X�̎��Ɏ����W�ƂȂ�܂��B���̎��́A�݂��ɕ��t�ɂ��锽�����Ɛ������̊Ԃɂ킸���ȃG�l���M�[�������邾���ŁA����̉����������ɑ��ʂɑ��݂���Ƃ������Ƃ������Ă��܂��B
![]()
(6) �����t�萔
�@���Ɏ����悤�ȉt�ω��ɂ����āAA�`D�����ׂċC�̂̏ꍇ�A�����Z�x�̑���ɁA���t��Ԃɂ����镪����p���āA���t�萔��\�����Ƃ�����܂��B������u�����t�萔(pressure equilibrium constant)�v�Ƃ����AKp�̋L���ŕ\���܂��B���̂悤�Ɉ����t�萔Kp��p���闝�R�́A�C�̔����̏ꍇ�́A�Z�x��舳�͂̕������肵�₷������ł��BA�̈��͂�PA�AB�̈���PB�AC�̈��͂�PC�AD�̈��͂�PD�Ƃ���ƁA
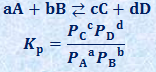
�e�C�̂̔Z�x�́A�P�ʑ̐ϓ�����̕����̃����ŕ\�����̂ŁA���z�C�̂̏�ԕ�����PV��nRT���A�����t�萔Kp�́A���̂悤�ɔZ�x���t�萔K�ŕ\�����Ƃ��ł��܂��B

����āA���xT�����ł���AK�͈��ŁA�܂�RT�����ł��邩��A�����t�萔Kp�̒l�����ɂȂ邱�Ƃ�������܂��B�C�̔����̏ꍇ�́A���̂悤�Ɉ����t�萔Kp���g�����Ƃ������Ȃ邱�Ƃɒ��ӂ��܂��傤�B
(7) ����V���g���G�̖@��
���w�����́A�������̃G���^���s�[H���������A�������̃G���g���s�[S���傫���قǁA���̏�Ԃ��������₷���Ƃ������ƂɂȂ�܂��B���Ȃ킿�A����2�̈��q�����킹�����R�G�l���M�[G���������قǁA�����������͈���ɂȂ�܂��B���������āA���R�G�l���M�[G���A���ӂƉE�ӂœ������Ƃ����A���t��Ԃł���Ƃ������Ƃ��ł��܂��B
�Ƃ���ŁA�G���g���s�[S�́A���G���̎w�W�ɂȂ�l�ł��B���̂��߁A1���q������̎��R�ȋ�Ԃ��傫���قǁAS�͑傫���Ȃ�܂��B�܂�A�G���g���s�[S�́A���q�̔Z�x�ƕ��̑��ւ�����܂��B����ŁA���͂�傫������ƁA�n���\�����闱�q�Ԃ̋������Z���Ȃ�A�Z�x���傫���Ȃ��āA�G���g���s�[S�ɉe����^���܂��B�܂��A���xT�́A�G���g���s�[S�Ƃ̐ςł���TS�̌`�ŁA���R�G�l���M�[G�Ɋւ���Ă��܂��B�ȏ�̂��Ƃ��A���t���x�z����v���ŁA�O�E����ω������邱�Ƃ��ł���̂́A�u�Z�x����ͥ���x�v��3���q�ł���Ƃ�����������܂��B�Ⴆ�A���fN2�Ɛ��fH2����A�����j�ANH3���������锽���́A�G���^���s�[H���������锭�M�����ł���A�܂��G���g���s�[S���������锽���ł��B
N2(�C)�@�{�@3H2(�C)�@���@2NH3(�C)�@�@ ��H ���|92 kJ
���̔����͉t�����Ȃ̂ŁA���t��Ԃ��牷�x���グ��ƁA�����͋t�����̌����ɐi�݂܂��B�܂��A�n�̈��͂��グ��ƁA�����͐������̌����ɐi�݁A���ꂼ��V���ȕ��t��ԂɂȂ�܂��B���̂悤�ɁA���t��Ԃɂ���n�ɉ��炩�̊O�I�ω����y�ڂ������ʁA���t��Ԃ�����āA�������������͋t���������炭�i�s���A���̌�ɐV���ȕ��t��ԂƂȂ錻�ۂ��A�u���t�ړ�(mobile equilibrium)�v�Ƃ����܂��B�����āA1884�N�Ƀt�����X�̉��w�҂ł��郋��V���g���G�́A���̕��t�ړ��̌����ɂ��āA���̕\.3�̂悤�ȋK���������܂����B
�\.3 ����V���g���G�̔��������@��
|
�^����O�I�ω� |
�����̐i�s���� |
|
���镨���̔Z�x���グ�� |
���̕����̔Z�x����������������� |
|
���镨���̔Z�x�������� |
���̕����̔Z�x������������� |
|
���x���グ�� |
�z�M����(��H��0)�� |
|
���x�������� |
���M����(��H��0)�� |
|
�C�̂����k����i���͂��グ��j |
�C�̗��q���̌��������� |
|
�C�̂�c��������i���͂�������j |
�C�̗��q���̑��������� |
��ʓI�ɁA�t���������t��Ԃɂ���Ƃ��A�������(�Z�x����ͥ���x)��ω�������ƁA�����ω��̉e����a�炰������ɔ������i�݁A�V���ȕ��t��ԂɂȂ�܂��B�������ʓI�ɁA�u����V���g���G�̖@��(Le Chatlier's law)�v�Ƃ����܂��B�����ω��̉e����a�炰������Ƃ́A�����ω��̌��ʂ�ł����������̂��Ƃł��B�Ⴆ�A���镨���̔Z�x��傫������A���̔Z�x����������������ɔ������i�݁A���x���グ��A�M���z����������ɔ������i�ނ��Ƃ��Ӗ����܂��B����V���g���G�̖@���́A���w���t����łȂ��A�n�t��C�t���t�Ȃǂ́A�����ω��ɂ����镽�t�ł����藧���܂��B�܂��A����V���g���G�̖@���ɂ����ẮA���̂��Ƃɒ��ӂ���K�v������܂��B
(i) �ő̂̐�Ηʂ͕��t�ړ��Ɩ��W�ł���
�@�Ⴆ�A�n�t�ɂ���O�a�H�����ɁA�����i�g���E��NaCl(��)�������Ă��A���t�ړ��͋N���炸�A[Na+]��[Cl-]�͈��ł��B���̗��R�́A�����i�g���E��NaCl(��)�̂悤�Ȍő̂ł́A�\�����q���т�����Ƌl�܂���������Ԃł���A�P�ʑ̐ϓ�����̗��q���A�܂�[NaCl(��)]��ς��邱�Ƃ́A������s�\������ł��B
NaCl(��)�@�{�@aq�@⇄�@Na+ (aq)�@�{�@Cl- (aq)
(ii) �����ɖ��W�ȕ����������Ă��A�Z�x�≷�x�����Ȃ�Ε��t�͈ړ����Ȃ�
�@��Ƃ��āA��_���Y�fCO2��Y�fC�ŊҌ����āA��_���Y�fCO���������镽�t�������l���܂��B���̌n�ɑ̐ψ��ŃA���S��Ar��������ꍇ�ƁA���͈��ŃA���S��Ar��������ꍇ�ŁA���t�ɂǂ̂悤�ȉe�����o�邩���l���܂��傤�B
CO2(�C)�@�{�@C(��)�@ ⇄�@2CO(�C)
(ii-1) �̐ψ���Ar��������
�@�̐ψ��ŃA���S��Ar��������ƁA�n�̑̐�V�����Ȃ̂ŁA���z�C�̂̏�ԕ�����P�SV��n�SRT���A�S��P�S�͑傫���Ȃ�܂��B�������A�̐�V�����ł���ȏ�A������(CO2, CO)�̕����͕ω����܂���B�e�C�̂̕����ɕω����Ȃ��̂ŁA�̐ψ��ŃA���S��Ar�������Ă��A���t�͈ړ����܂���B
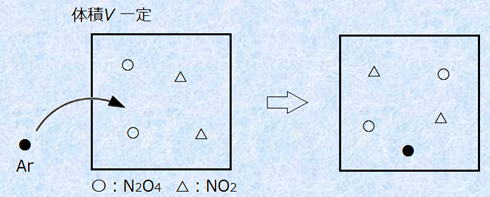
�}.10 �̐ψ��ŃA���S��Ar���������ꍇ
(ii-2) ���͈���Ar��������
�@���͈��ŃA���S��Ar��������ƁA�n�̈���P�����Ȃ̂ŁA���z�C�̂̏�ԕ�����PV�S��n�SRT���A�S�̐�V�S�͑傫���Ȃ�܂��B���������āA�̐�V���傫���Ȃ邱�Ƃɂ��A�e�C�̂̔Z�x����������̂ŁA������(CO2, CO)�̕����͏������Ȃ��Ă��܂��܂��B�܂�A���͈���Ar��������ƁA�e�C�̂̕����͏������Ȃ�̂ŁA�C�̗��q���������ł���E�֕��t���ړ����܂��B
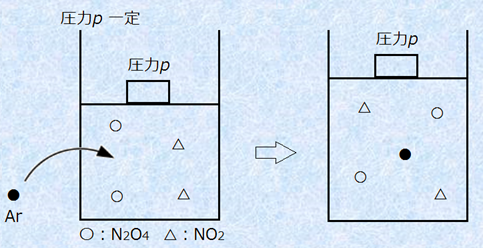
�}.11 ���͈��ŃA���S��Ar���������ꍇ
(ii-3) �G�}�������Ă����t�͈ړ����Ȃ�
�G�}�́A�����̎d�g�݂�ς��āA�������G�l���M�[����菬�����o�H�Ŕ������i�݂悤�ɂ��܂��B����t�����ŐG�}���������Ƃ��A�������G�l���M�[����E�����������Ȃ�Ƃ��āA�G�}���������Ƃ��̑��x�萔��k1cat, k2cat�Ƃ���ƁA�A���j�E�X�̎�![]() ���A���̂悤�ɂȂ�܂��B
���A���̂悤�ɂȂ�܂��B
![]()
![]()
���Ȃ킿�Ak1cat, k2cat�́Ae��E/RT�Ƃ����������������傫���Ȃ�Av1, v2���܂��A���������ő傫���Ȃ�̂ł��B�܂�A�G�}�͐��t�������Ƃ��ɔ������x��傫�����āA���t��ԂɒB����܂ł̎��Ԃ�Z��������̂́A���t���ړ������邱�Ƃ͂���܂���B
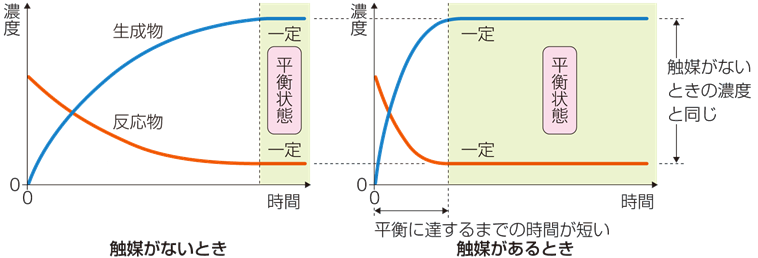
�}.12 �G�}�́A���t�ɒB����܂ł̎��Ԃ�Z������
(8) ���w���t�ɂ����锽���G���^���s�[
���w���t�𗘗p���邱�ƂŁA���̔��������M�����Ȃ̂��A�z�M�����Ȃ̂������f�ł���悤�ɂȂ�܂��B�Ⴆ�A�t�����ł���A(�C)�{B(�C)⇄C(�C)�̕��t���l�����Ƃ��A�������̃G���g���s�[�ω���S�́A���q������������̂���S��0�ł��B����āA�M�u�X�̎��R�G�l���M�[��G����H-T��S���A-T��S�̍��͐��ɂȂ�̂ŁA������H��0���ƕK�R�I����G��0�ƂȂ�A�����������R�ɐi�܂Ȃ��Ƃ������ƂɂȂ�܂��B�����������R�ɐi�܂Ȃ��Ƃ������Ƃ́A�t�������������Ȃ��Ȃ�Ƃ������ƂȂ̂ŁA���̔����ɂ����ẮA���Ȃ��Ƃ���H��0�ł��邱�Ƃ��ۏ���܂��B�܂�A���t��Ԃɂ��邱�̔����́A���M�����ł��邱�Ƃ�������̂ł��B
�\.4 ���t��Ԃɂ�������S����H�̊W
|
����������S |
����������H |
�� |
|
��S��0�i���G�������j |
��H��0�i�z�M�����j |
2SO3(�C)�@ ⇄�@2SO2(�C)�@�{�@O2(�C)�@�|�@Q kJ |
|
��S��0�i���G�������j |
��H��0�i���M�����j |
2NO(�C)�@�{�@O2(�C)�@ ⇄�@2NO2(�C)�@�{�@Q kJ�@ |
�\.4�Ŏ������W�́A�O���܂ł��t�����ł������藧���Ȃ��Ƃ������Ƃɒ��ӂ��Ȃ���Ȃ�܂���B���t��Ԃɂ�����t�����ɂ��ẮA���M����(��H��0)�̔����́A�K�����G�����������A�z�M����(��H��0)�̔����ł́A�K�����G�����������锽���ɂȂ��Ă��܂��B�܂�A���t�����ɂ����ẮA���t�����̂ǂ��炩���u���M�����v�ŁA�������u���G�������傷�锽���v�ƂȂ�̂ł��B
�E�Q�l����
1) �ΐ쐳���u�V���n�̉��w(��)�v�x�䕶��(2005�N���s)
2) ꎓ���/������/�R�{����/��19���u���w�v�[�ъ�(2012�N���s)
3) ���[�g�����h��W���[���Y�u�W���[���Y�L�@���w(��)�v�������w���l(2000�N���s)
4) �n�Ӑ�/�k�����F �����u���Z�ŋ���肽���������w�v���{�]�_��(2008�N���s)