�E�A���~�j�E�����p�����A�{�K�h���萔�̑���
�y�ڎ��z
�@ �A���~�j�E�����d�q�V���ɍڂ��āA���ʂ�ʂ�B
�A �A���~�j�E������^�R���Ŕ���A�݂邹��悤�ɂ���B
�B 50 mL�r�[�J�[�ɐ����50 mL����A�d�q�V���ɍڂ��āA�\����0�ɂ���B
�C �^�R���������āA�A�̃A���~�j�E����𐅒��ɐZ���ĐÎ~�����A�\�����ʂ��L�^����B���̂Ƃ��A�A���~�j�E���r�[�J�[�̒�ɕt���Ȃ��悤�ɒ��ӂ��邱�ƁB

�}.1 �A���~�j�E������^�R���Œ݂邵�A�����ŐÎ~������
(2) ���_
�@�Ñ�M���V�A�̕����w�҂ł���A���L���f�X�́A�u���̒��̕��̂́A���̕��̂������̂��Ă��闬�̂̏d���Ɠ����傫���ŁA������̕��͂���v�Ƃ����@�������܂����B������A�u�A���L���f�X�̌����v�Ƃ����܂��B
�A���~�j�E�������ɂ���Ƃ��A�A���~�j�E����́A���ꂪ�����̂��Ă��鐅�̏d���Ɠ����傫���ŁA������̕��� ��Vg ���܂��B����ŁA���ƃr�[�J�[�́A�����傫���ŁA�������̕��͂̔���p ��Vg ���܂��B�܂�A���ƃr�[�J�[�ɂ�����͂́A���ƃr�[�J�[�̏d�� Mg�A������̐����R�� N�A���͂̔���p ��Vg ��3�ł��B
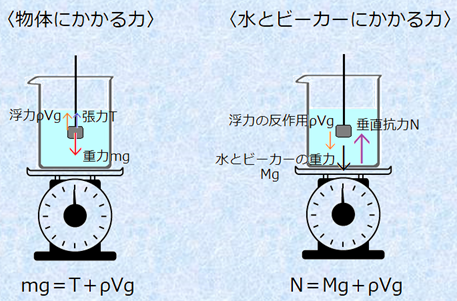
�}.2 �q���̂ɂ�����́r����сq���ƃr�[�J�[�ɂ�����́r�̂荇��
���̂����A�����v���ł���̂́A�����R�� N �ł��B�������A�����R�� N �̒P�ʂ́uN�v�ł��邵�A���̕\�����ʂ̒P�ʂ́ug�v�Ȃ̂ŁA���l�͊��S������v�͂��܂���B�܂��A���������B�́A���ƃr�[�J�[�̏d�� Mg ��0�ɂ�����̂ł��B������A���������C�ɂ����āA�͂̂荇���̎��𗧂Ă�ƁA���̂悤�ɂȂ�܂��B
![]()
![]()
�@���� ![]() ���A�u���̕\�����ʁv��\���Ă��܂��B������A���̖��x �� �ŁA���̕\������
���A�u���̕\�����ʁv��\���Ă��܂��B������A���̖��x �� �ŁA���̕\������ ![]() �����邱�ƂŁA�A���~�j�E����̑̐� V �����߂��܂��B�A���~�j�E����̎��ʂ́A��������@�̂悤�ɒ��ڑ��邱�Ƃ��ł���̂ŁA���̎�������́A�A���~�j�E����̖��x���Z�o���邱�Ƃ��ł��܂��B
�����邱�ƂŁA�A���~�j�E����̑̐� V �����߂��܂��B�A���~�j�E����̎��ʂ́A��������@�̂悤�ɒ��ڑ��邱�Ƃ��ł���̂ŁA���̎�������́A�A���~�j�E����̖��x���Z�o���邱�Ƃ��ł��܂��B
![]()
(3) ����
�@���̎����ł́A�A���~�j�E����Ƃ��āA������Д����˂��́u�A���~�j�E���T�C�R���v���g�p���܂����B���肪����ꍇ�́A��~�ʂł��������\�ł��B��������@����ю�������C�̌��ʂ́A���̂悤�ɂȂ�܂����B
�\.1 �A���~�j�E����̎��ʂƁA�A���~�j�E����̐����ł̎���
|
���������@ |
���������C |
|
�A���~�j�E����̎��� |
�A���~�j�E����̐����ł̎��� |
|
8.44 g |
3.11 g |
�@������A���̖��x��1.00 g/cm3�Ƃ���ƁA�A���~�j�E����̑̐ς́A���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
![]()
�@��������@���A�A���~�j�E����̎��ʂ�8.44 g�Ȃ̂ŁA���̃A���~�j�E����̖��x�́A���̂悤�ɂȂ�܂��B
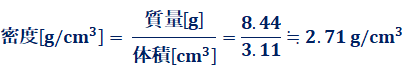
�A���~�j�E��Al�̒P�ʊi�q�́A���̐}.3�Ɏ����悤�ȁu�ʐS�����i�q�v�ł���A�i�q�萔(�P�ʊi�q��ӂ̒���)��4.05�~10—8 cm�ł��B�܂��A�ʐS�����i�q�̊i�q�����q���́A1/8�~8�{1/2�~6��4�ł��B
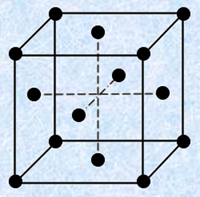
�}.3 �A���~�j�E��Al�̒P�ʊi�q�́A�u�ʐS�����i�q�\���v�����
������A�A���~�j�E���̌��q�ʂ�27.0�Ƃ���ƁA�A�{�K�h���萔 ![]() �́A���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
�́A���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
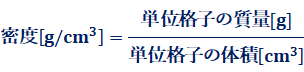
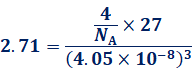
![]()