・結晶化学
【目次】
(1) 金属結晶
金属の陽イオンが規則正しく配列し、その間を自由電子が動き回りながら、これらがクーロン力で結びついている結晶を、「金属結晶(metal crystal)」といいます。金属の自由電子は、結晶内を自由に動き回ることができるので、このことが結合の安定性をもたらしています。一般的に金属は「金属光沢(metallic luster)」を持ちますが、これは可視光が自由電子により、反射散乱されるためです。また、金属は優れた電気伝導性と熱伝導性を持ちますが、これも自由電子に起因する性質です。自由電子は、電荷や熱の優れた運び手となることができるのです。さらに、金属は外部から力を加えても、変形するだけで割れないため、二次的に薄く箔状に広げられる「展性(malleability)」や、一次的に細長く線状に引き延ばされる「延性(ductility)」があります。これは、金属を叩くことによって結晶の層がずれて原子が移動しても、自由電子が接着剤のような役割をして、金属結合を保つためです。
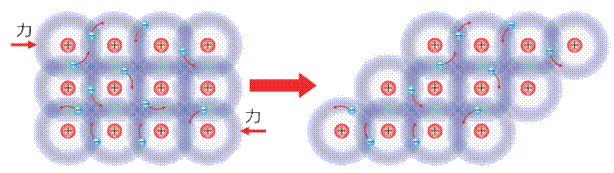
図.1 金属結合による展性と延性
金属の融点は様々ですが、一般的に典型元素の金属単体の融点は低く、遷移元素の金属単体の融点は高い傾向にあります。遷移金属の結晶における原子の大きさは、同周期のアルカリ金属やアルカリ土類金属に比べると小さく、遷移元素はd軌道やf軌道のように外部に広く分布する電子が金属結合に参加するため、金属結合が強固になって、融点が高くなるのです。なお、水銀Hg(m.p.-39℃)は常温で液体の金属ですが、ガリウムGa(m.p.30℃)やセシウムCs(m.p.28℃)も夏場の室温では融解して液体になる金属です。

図.2 ガリウムGaの融点は30℃と室温に近く、人の手の上で融解する
純物質の固体で、構成粒子が三次元的に規則正しく配列しているものを「結晶(crystal)」といいます。また、結晶内の粒子の配列を示したものを「結晶格子(crystal lattice)」といい、粒子配置の繰り返しの最小の単位構成を「単位格子(unit lattice)」といいます。結晶は、単位格子をいくらか繋げてマクロな状態にしたものです。したがって、単位格子の性質を知ることは大変重要であり、そこからマクロなレベルの結晶の性質を知ることができます。すなわち、単位格子での量の比と結晶のレベルでの量の比は常に等しいので、単位格子と結晶のレベルを量的に関係付けることができるのです。密度(g/cm3)・充填率(cm3/cm3)・組成比(個/個)などの値は、単位格子と結晶のレベルで同じ値になります。
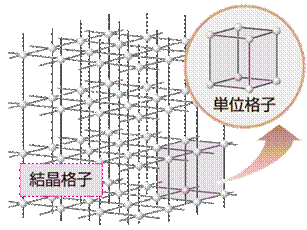
図.3 アルミニウムの単位格子と結晶
金属結晶は、金属結合によって安定化しています。そのため、それぞれの金属原子は、できるだけ多くの金属原子と金属結合した方が全体的に安定になりやすいです。したがって、金属結晶は配位数の大きい密な構造になることが多く、ほとんどの金属単体は「体心立方格子(body-centered cubic lattice)」・「面心立方格子(face-centered cubic lattice)」・「六方最密構造(close-packed hexagonal lattice)」のいずれかの結晶格子をとっています。それぞれの結晶格子の特徴は、次の表.1の通りです。
表.1 主な結晶格子の特徴
|
分類 |
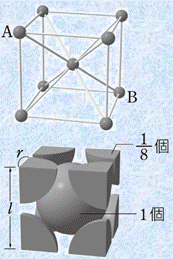
体心立方格子 |
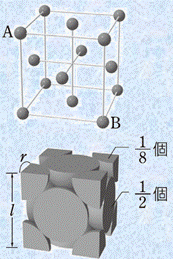
面心立方格子 |
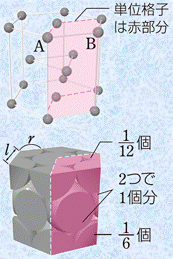
六方最密構造 |
|
単位格子 |
|
|
|
|
格子内 原子数 |
|
|
|
|
配位数 |
8 |
12 |
12 |
|
lとrの関係 |
|
|
|
|
充填率 |
68% |
74% |
74% |
|
金属の例 |
Na、Kなど |
Al、Cu、Agなど |
Mg、Znなど |
(i) 単位格子一辺の長さlと原子半径rの関係
結晶の単位格子の形と大きさを表すパラメーターを「格子定数(lattice constant)」といいます。一般的には、単位格子の各綾の長さ(3つの結晶軸の各方向にそった繰り返しの周期)のa, b, cと、それらが互いになす角α, β, γで表すことが多いです。しかし、高校化学で扱う金属の単位格子は、ほとんどが体心立方格子もしくは面心立方格子のような立方体形になるので、格子定数としてaの値だけを与えることも多いです。高校化学では、一般的に格子定数といったら、単位格子の一辺の長さのことだと思っても構いません。
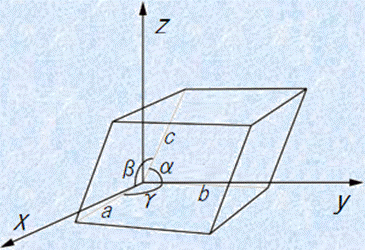
図.4 格子定数
単位格子一辺の長さをlとすると、原子半径rとの間には、どのような関係があるでしょうか?体心立方格子では、すべての原子が密に充填されていて、中心の原子と各頂点の原子とが接しているとすると、「![]() 」という関係が成り立ちます。これより、単位格子一辺の長さlから原子半径rの値を求めることができるのです。
」という関係が成り立ちます。これより、単位格子一辺の長さlから原子半径rの値を求めることができるのです。
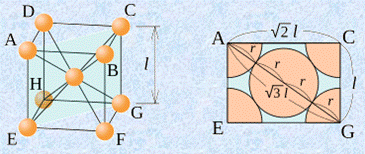
図.5 体心立方格子の一辺の長さlと原子半径rの関係
一方で、面心立方格子では、すべての原子が密に充填されていて、各面の中心の原子と各頂点の原子とが接しているとすると、「![]() 」という関係が成り立ちます。
」という関係が成り立ちます。
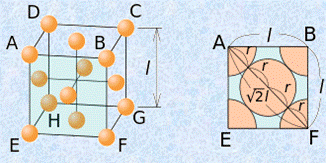
図.6 面心立方格子の一辺の長さlと原子半径rの関係
(ii) 配位数
「配位数(coordination number)」とは、結晶中の1つの原子から見た最近接粒子数のことです。例えば、体心立方格子では、中心の原子に対して8個の原子が接しているので、体心立方格子の配位数は8になります。一方で、面心立方格子では、中心の原子が存在しないので、最近接粒子数は何個なのか一見すると分かりにくいです。しかし、次の図.7のように面心立方格子を2つ繋げて考えると、分かりやすくなります。図.7のように考えると、中心の原子から見て12個の原子が接していることが分かります。つまり、面心立方格子の配位数は12になります。また、六方最密構造についても、中心の原子が存在しないので、単位格子を2つ繋げて考えます。このように考えると、六方最密構造の配位数も12であることが分かります。

図.7 面心立方格子と六方最密構造の配位数
ここで、面心立方格子と六方最密構造の違いについても確認しておきましょう。両者の配位数は共に12ですが、この数字が意味することは、両者の構造は数学的には似た構造であるということです。「そんな馬鹿なことはあるか。どう見ても違う構造ではないか」と思うかもしれませんが、面心立方格子を斜め45°の角度から見ると、次の図.8のように六方最密構造と同じような形になるのです。両者の構造の違いは、構造の繰り返しのパターンにあります。すなわち、面心立方格子では構造の繰返しパターンが「ABCABC・・・」の3層周期であるのに対して、六方最密構造では構造の繰返しのパターンが「ABABAB・・・」の2層周期となっているのです。
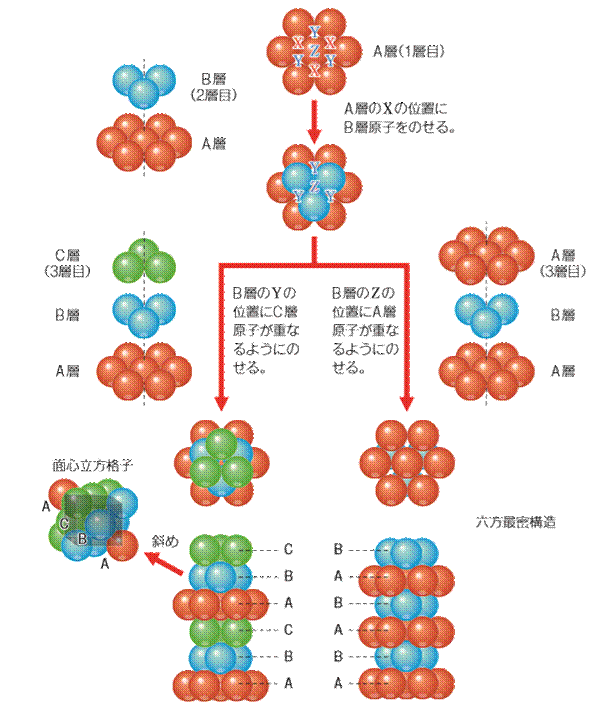
図.8 面心立方格子と六方最密構造の違い
(iii) 充填率
結晶構造の体積のうち、原子がどれだけの割合を占めているのかを表す値を「充填率(packing ratio)」といいます。一般的に配位数が多い構造ほど、原子が密に充填されていることになるので、充填率は大きくなります。充填率は、次のようにして計算で求めることができます。

これより、体心立方格子と面心立方格子の充填率を求めてみましょう。原子を変形しない完全な球体と仮定して、単位格子一辺の長さをl、原子半径をrとします。体心立方格子の場合では、原子半径は![]() 、格子内原子数は2個なので、次のようになります。
、格子内原子数は2個なので、次のようになります。
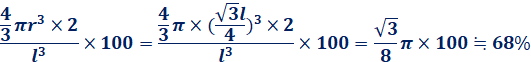
面心立方格子の場合では、原子半径は![]() 、格子内原子数は4個なので、次のようになります。
、格子内原子数は4個なので、次のようになります。
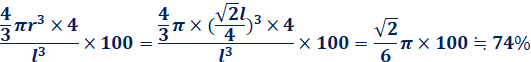
これより、体心立方格子の充填率は約68%、面心立方格子の充填率は約74%であることが分かります。面心立方格子は最も密な構造なので、この74%が充填率の極大であることも分かります。
なお、六方最密構造の充填率は、次のようにして求めます。まず、六方最密構造の六角柱の体積を求めましょう。六角柱の体積は、底面である正六角形の面積と高さとの積で求めることができます。六角柱の底面積は、一辺が2rの正六角形6個分に相当するので、次のようになります。
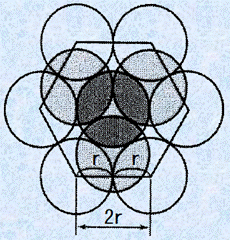
図.9 六方最密構造を上から見た図
![]()
次に、六角柱の高さを求めてみます。次の図.10の色の濃い球の中心を結ぶと、一辺が2rの正四面体になります。この正四面体の高さhの2倍が六角柱の高さに相当することから、次のように求めることができます。
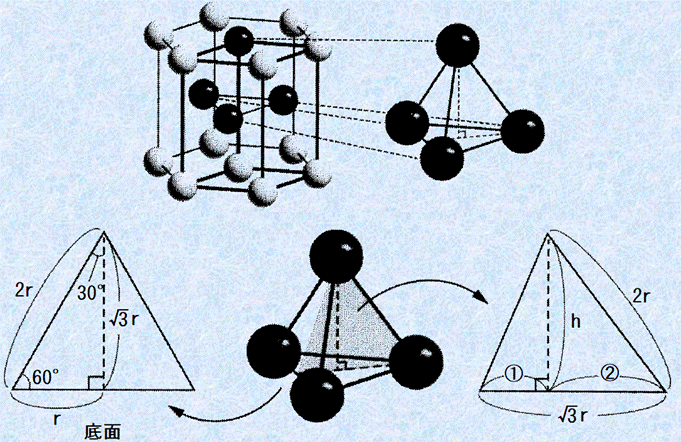
図.10 六方最密構造の正四面体に注目する
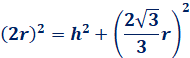
![]()
この六角柱には、六方最密構造の単位格子3個分の金属原子が含まれるので、計6個の金属原子が含まれています。これより、六方最密構造の充填率は、次のようになります。
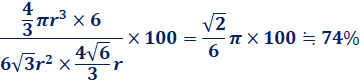
(iv) ケプラー予想
一定サイズの小球で大きな容器を一杯にしたいとします。このとき、球を無造作に投げ込んでいくと、充填率は約65%になることが実験的に確かめられています。これよりも充填率を向上させるためには、球の隙間ができるだけ少なくなるようにして、球を敷き詰めていく必要があります。17世紀を代表する天文学者であり、数学者でもあったヨハネス・ケプラーは、1611年に「等しい大きさの球で空間を充填するとき、充填率は面心立方格子ならびに六方最密構造を超えることはない」という仮説を立てました。この問題は、彼の名前にちなんで、「ケプラー予想(Kepler conjecture)」と呼ばれています。ケプラーは、数学者のトーマス・ハリオットと共に、「船倉に砲弾を効率的に詰め込む方法」を考えており、このケプラー予想に至ったのでした。わざわざ「ケプラー予想」などと大仰な名前が付いているのは、これがとんでもない超難問であったからです。こんな問題、簡単に証明できるだろうと手を出した数学者たちはことごとく失敗し、一見するとはるかに難しいように見える他の問題が解けたあとも、超難問として数学の世界に君臨し続けました。

図.11 ケプラーは球を敷き詰めたとき、充填率は74%が最大となると予想したが、400年もの間未解決だった
数学者のトーマス・ヘイルズは、1992年からコンピュータを駆使してこの問題に取り組み、1998年に300ページ以上にも及ぶ証明を発表しました。しかし、12人の数学者が4年をかけてチェックしても、まだ完全な決着には至らず、形式的な証明が終了したのは、ケプラー予想から400年以上もあとの2014年のことでした。ケプラー予想は、長年数学者たちを悩ませてきましたが、現在ではほぼ正しいことが証明されています。このケプラー予想を用いれば、このような面白い思考実験ができます。
「教室の中にサッカーボールは最大で何個入るだろうか」
教室の体積は、縦25 m×横10 m×高さ4 m=1000 m3とします。サッカーボールは完全な球体と仮定し、半径を0.1 mとします。ケプラー予想によれば、充填率は0.74が最大となるので、教室の中に入るサッカーボールの数を計算すると、次のようになります。
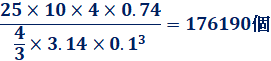
これより、「教室の中にサッカーボールは最大で18万個入る」ということが概算できます。このように実際に調査するのが困難なことを、いくつかの手がかりをもとに概算することを「フェルミ推定(Fermi estimate)」といいます。フェルミ推定は、コンサルティング会社や外資系企業などの面接試験で用いられることがある他、欧米では学校教育で科学的な思考力を養成するために用いられることもあります。
(iv) 結晶の密度
密度は、単位体積当たりの質量で表されるので、結晶の絶対量に無関係な値です。すなわち、結晶は単位格子の繰り返しであるから、結晶の密度は単位格子の密度に等しいです。よって、次のような関係が成り立ちます。

一般的に結晶の密度d g/cm3は、次のようにして求めることが多いです。アボガドロ定数をNA、体積をa3 cm3、原子量をMとすると、次のようになります。
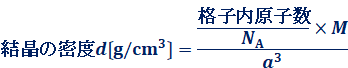
(2) イオン結晶
多数の陽イオンと陰イオンが、クーロン力によるイオン結合により、立体的に規則正しく配列した結晶を「イオン結晶(ionic crystal)」といいます。イオン結合は、金属結合に匹敵するぐらい強い結合です。そのため、イオン結晶は一般的に融点が高く、硬い性質を持つ場合が多いです。しかし、一方でイオン結晶は、一定の面で綺麗に割れやすい性質も持ちます。この性質を「へき開性(cleavage)」といいます。これは、イオン結晶に外力が加わって、原子の層がずれると、同符号のイオンが並んで、互いに反発し合うためです。
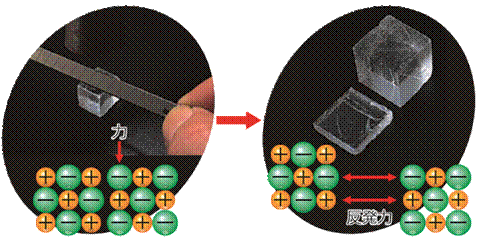
図.12 イオン結晶のへき開性
また、通常イオン結晶は、固体では電気を導かず絶縁体ですが、融解した液体やその水溶液はイオンが移動できるので、電気伝導性があります。イオン結晶は、基本的には常温で固体と考えていいですが、常温で液体のものもあり、これを「イオン液体(ionic liquid)」といいます。イオン液体は、水でも油でもない「第3の液体」として、現在注目されています。イオン液体は、大きくて複雑な有機イオン同士がイオン結合したものです。木材の成分であるリグニンを溶かすイオン液体が開発されており、これによって木材からヘミセルロースとリグニンを分離することが可能になります。木材から得たリグニンは、カーボンナノチューブの原料になるといいます。

図.13 イオン液体は、常温で液体の塩である
イオン結晶の結合エネルギーの指標の1つに、「格子エネルギー(lattice energy)」というものがあります。格子エネルギーとは、固体結晶の状態にある陽イオンと陰イオンを、完全に切り離してばらばらの気体状態にするのに必要なエネルギーのことです。Am+ とBn− のイオン結晶をAaBbとすると、格子エネルギーQ kJ/molは、次のように表せます。
AaBb(固体) = aAm+(気体) + bBn−(気体) − Q kJ
この格子エネルギーが大きいほど、結晶はエネルギー的に安定になり、融解や沸騰を起こしにくくなります。格子エネルギーは、構成イオンの半径が小さく、イオンの価数が大きいほど、大きくなります。これは、イオン半径が小さく、イオンの価数が大きいほど、イオン間に働くクーロン力が大きくなるためです。粒子間の相互作用が強いほど、物質の融点や沸点は大きくなるのです。
表.2 主なイオン結晶の融点と沸点
|
化学式 |
融点〔℃〕 |
沸点〔℃〕 |
|
NaF |
993 |
1,704 |
|
NaCl |
800 |
1,413 |
|
NaBr |
755 |
1,390 |
|
NaI |
651 |
1,300 |
|
CaF2 |
1,360 |
2,500 |
|
BaCl2 |
1,280 |
2,260 |
|
CaO |
2,572 |
2,850 |
|
BaO |
1,923 |
2,000 |
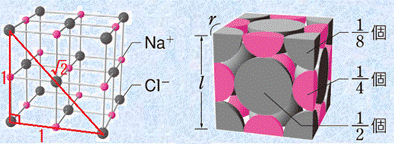
イオン結晶の結合力は、主にイオン間のクーロン力によります。そのため、各イオンは、できるだけ多くの異符号のイオンで囲まれた方が安定になります。陽イオンの周りの陰イオンの数を「配位数(coordination number)」といい、配位数はイオン半径比r+/r− によって支配されます。構成イオンは、ナトリウムイオンNa+ やカルシウムイオンCa2+、塩化物イオンCl− のような単原子イオンのみである場合も、その一部または全部が炭酸イオンCO32− やアンモニウムイオンNH4+ のような多原子イオンである場合もあります。代表的なイオン結晶として、岩塩型と塩化セシウム型の結晶格子の特徴を示します。
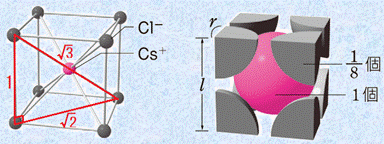
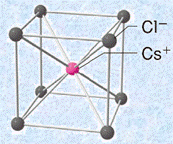
表.3 岩塩型と塩化セシウム型の結晶格子の特徴
|
|
岩塩型構造 |
塩化セシウム型構造 |
|
単位格子 |
|
|
|
組成式 |
NaCl |
CsCl |
|
格子内 粒子数 |
|
Cs+:1個
|
|
配位数 |
Na+:6 Cl−:6 |
Cs+:8 Cl−:8 |
|
lとrの関係 |
|
|
(i) 限界半径比
岩塩型構造と塩化セシウム型構造を比較したとき、塩化セシウム型構造の方が安定になります。これは、一般的にイオン結晶では、互いに接する反対符号のイオンの数(配位数)が多いほど安定になるからです。しかし、一般的に陽イオンよりも陰イオンの方が大きいため、陽イオンの半径が陰イオンに比べてかなり小さい場合では、陰イオン同士が接触するようになります。同種のイオンは、互いに接したり重なったりすると、クーロン力による反発で不安定になります。そこで、すべてのイオン結晶は、陰イオン同士が接触しないような結晶構造を取るようになります。あるイオン結晶がどちらの結晶構造になるのかは、次のイオン半径比r+/r− を考えることで分かります。
![]()
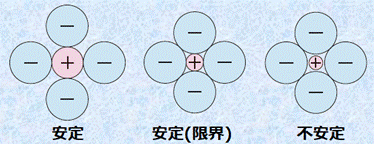
図.14 陽イオンと陰イオンの大きさの関係
まずは、塩化セシウム型構造について考えてみましょう。陽イオンが小さくなっていくと、いずれ陰イオン同士が接触するようになります。この状態は、ちょうど陰イオンの間に陽イオンが入り込んだような構造です。この状態からさらに陽イオンが小さくなっても、陽イオンと陰イオンの互いの中心間距離は変わらないため、構造が不安定になるだけです。そこで、この陽イオンと陰イオン同士が密着した状態のイオン半径比r+/r− を、特に「限界半径比(critical radius ratio)」といいます。塩化セシウム型構造の限界半径比は、次のようになります。
![]()
![]()
![]()
また、岩塩型構造の限界半径比も、次のようにして求めることができます。
![]()
![]()
![]()
イオン結晶は、基本的には配位数の大きい塩化セシウム型構造になろうとします。しかし、塩化セシウム型構造の限界半径比は0.73と比較的大きいため、陽イオンの大きさが陰イオンの0.73倍未満(0.41r−≦r+<0.73r−)の場合には、限界半径比が0.41の岩塩型構造になろうとします。つまり、r+/r−≧0.73の陽イオンが比較的大きいイオン結晶の場合には塩化セシウム型構造が安定であり、0.73>r+/r−≧0.41の陽イオンが比較的小さいイオン結晶の場合には岩塩型構造が安定になるのです。ただし、塩化カリウムKClのような例外(r+/r−=0.901だが岩塩型構造)も一部あるので、注意が必要です。
![]()
![]()
(3) 分子結晶
多数の分子が分子間力によって集合し、規則正しく配列してできた結晶を「分子結晶(molecular crystal)」といいます。分子結晶は、分子間の相互作用が弱いため、一般的に融点が低くて軟らかいです。分子間力には、ファンデルワールス力や水素結合などがあり、分子結晶を結合力の違いから「ファンデルワールス結晶(Van der Waals' crystal)」や「水素結合結晶(hydrogen bonding crystal)」とさらに分類する場合もあります。
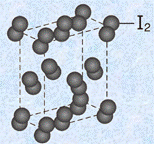
代表的なファンデルワールス結晶には、ドライアイスCO2・ナフタレンC10H8・ヨウ素I2などがあります。これらの結晶は、一般的に融点が低くて軟らかく、昇華性を持つ場合が多いでです。昇華性を持つ結晶が多い理由は、わずかに温度が上がっただけでも、分子の熱運動がファンデルワールス力を上回り、分子が容易に結晶から飛び出すようになるからです。また、ファンデルワールス結晶は、電気的に中性な分子からできており、固体でも液体でも電気を通しません。
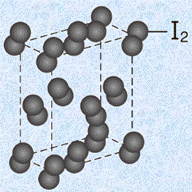
図.15 ヨウ素I2の結晶
代表的な水素結合結晶には、水H2Oがあります。水H2Oの結晶である氷は、水分子が分子間に働く水素結合で、1つの水分子の周りに4つの水分子が配置されるような正四面体構造の結晶を作ります。そのため、氷はかなり隙間の多い構造となり、充填率はたったの32%しかありません。氷が融けて液体になると、分子間の水素結合が切れて体積が小さくなるので、氷の密度は液体よりも小さくなります。固体である氷が液体の水に浮かぶのはこのためです。固体の密度が液体よりも小さいことは、水の特徴的な性質の1つです。
具体的な数値を用いて説明すると、0℃における1 molの氷の水素結合をすべて切断するエネルギーは46.8 kJ/molですが、0℃の氷から0℃の水に状態変化するときの融解熱はわずか6.0 kJ/molです。このことは、0℃の水には87%近くの水素結合が切れずに存在しており、氷の正四面体構造がある程度維持されていることになります。なお、固体の密度よりも液体の密度の方が大きい物質を、一般的に「異常液体(abnormal liquid)」といいます。異常液体には、水H2Oの他にケイ素SiやゲルマニウムGeなどがあります。いずれも、固体状態のときは隙間の多い結晶構造を取る物質です。
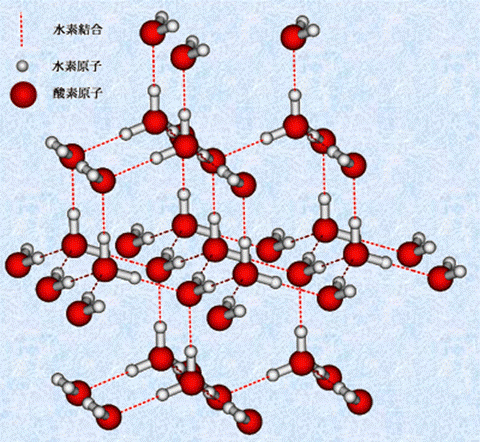
図.16 氷の結晶構造
水H2Oの密度は、温度によって若干変化します。固体の氷から液体の水へ変化する際、0℃より温度を上げていくと、分子間の水素結合が切れて、氷の結晶構造が崩れ、体積が減少する現象が起こります。また、温度を上げていくと、分子の熱運動が激しくなり、水分子の占める空間が増加する現象も起こります。温度が0〜4℃では、前者の効果が大きくて体積が減少し、温度が4℃以上では、後者の効果が大きくて体積は次第に増加するのです。この2つの相反する効果の兼ね合いで、水は4℃付近で最も体積が小さくなります。つまり、水の密度は4℃で最大となるのです。このときの水の密度は0.99997 g/cm3で、4℃以外の温度では、いずれもこの値よりも小さくなります。
表.4 水の密度(単位はg/cm3)
|
温度〔℃〕 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0.99984 |
0.99990 |
0.99994 |
0.99996 |
0.99997 |
0.99996 |
0.99994 |
0.99990 |
0.99985 |
0.99978 |
|
10 |
0.99970 |
0.99960 |
0.99950 |
0.99938 |
0.99924 |
0.99910 |
0.99894 |
0.99877 |
0.99859 |
0.99840 |
|
20 |
0.99820 |
0.99799 |
0.99777 |
0.99754 |
0.99730 |
0.99704 |
0.99678 |
0.99651 |
0.99623 |
0.99594 |
|
30 |
0.99565 |
0.99534 |
0.99502 |
0.99470 |
0.99437 |
0.99403 |
0.99368 |
0.99333 |
0.99296 |
0.99259 |
|
40 |
0.99221 |
0.99183 |
0.99143 |
0.99103 |
0.99062 |
0.99021 |
0.98979 |
0.98936 |
0.98892 |
0.98848 |
|
50 |
0.98803 |
0.98757 |
0.98711 |
0.98664 |
0.98617 |
0.98569 |
0.98520 |
0.98471 |
0.98421 |
0.98370 |
|
60 |
0.98319 |
0.98267 |
0.98215 |
0.98162 |
0.98109 |
0.98055 |
0.98000 |
0.97945 |
0.97889 |
0.97833 |
|
70 |
0.97776 |
0.97719 |
0.97661 |
0.97602 |
0.97543 |
0.97484 |
0.97424 |
0.97363 |
0.97302 |
0.97241 |
|
80 |
0.97178 |
0.97116 |
0.97053 |
0.96989 |
0.96925 |
0.96861 |
0.96796 |
0.96730 |
0.96664 |
0.96597 |
|
90 |
0.96530 |
0.96463 |
0.96395 |
0.96327 |
0.96258 |
0.96188 |
0.96118 |
0.96048 |
0.95977 |
0.95906 |
※ 縦の欄は10の位、横の欄は1の位を示す
水H2Oが持つこの特異な性質は、身近でも実感することができます。例えば、冬に厚い氷で覆われた湖の底では、密度が最大となる4℃前後の水が存在し、そこで魚などの水生生物が生息しています。水面に氷の層ができれば、氷の層が断熱材の働きをして、外気が身を切るような寒い夜でも、水が底まで凍ってしまうのを防いでくれます。もし水H2Oが普通の物質のように、温度が下がるにつれて体積が小さくなるとしたら、それは水生生物にとって悲劇です。冷たい液体は底にたまり、底から凍っていくことでしょう。断熱材の働きをするものがないので、やがて湖は上から下まで、がちがちに凍ってしまいます。これでは、水中の生物は生きていくことができないでしょう。ちなみに、ジュエリーブランドの「4℃」もこれに由来し、4℃という水温のように、潤いをもたらす商品を提供したいという思いが込められているそうです。

図.17 氷上の穴釣りでワカサギを獲ることができる
なお、氷には、温度や圧力によって多くの結晶構造があります。普通に見られる氷は、「氷I」と呼ばれているものです。高圧下の氷が普通の氷と違うことを示したのは、ハーバード大学の物理学者であるパーシー・ブリッジマンです。ブリッジマンは、超高圧装置の発明と高圧物理学の研究で、1946年にノーベル物理学賞を受賞しています。ブリッジマンは超高圧発生装置を用いて、世界で初めて水H2Oを室温のまま1万気圧以上まで圧縮して、高圧氷を作ることに成功しました。1万気圧付近でできる氷は、「氷VI」と呼ばれるものです。そして、さらに圧縮して2万気圧付近でできる氷が、「氷VII」と呼ばれるものです。氷VIIは、100℃を超えても融けない「熱い氷」で、密度は普通の氷の2倍近くあります。これらの高圧氷は、海王星などの巨大惑星に存在することが予想されています。
(4) 共有結合の結晶
多数の原子が共有結合で連続的に繋がり、原子が規則正しく配列した結晶を「共有結合結晶(covalent bond crystal)」といいます。代表的な例としては、ダイヤモンドC・黒鉛C・イ素Si・二酸化ケイ素SiO2・炭化ケイ素SiCなどがあります。共有結合結晶は、硬度が大きくて融点も高いのが特徴です。また、価電子がすべて共有結合に使われているため、電気を通しません(黒鉛は例外的に電気を通します)。さらに共有結合は、イオン結合や金属結合とは異なり、結合に方向性があるため、できた結晶の配位数は小さく、構造はあまり密ではありません。
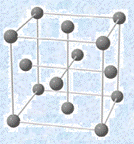
ここでは、代表的なダイヤモンドCの構造について説明しましょう。ダイヤモンドCは、炭素原子が共有結合で、1つの炭素原子の周りに4つの炭素原子が配置されるような正四面体構造の結晶を作ります。ダイヤモンドCの結晶では、単位格子が三次元的に繰り返し配列していて、ダイヤモンドCの単位格子は、次の図.18で示すような立方体になります。
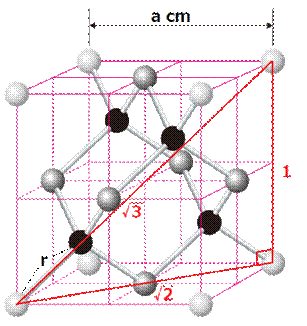
図.18 ダイヤモンドCの結晶格子
ダイヤモンドCの格子定数をa cm、炭素原子間の距離をr cmとして、ダイヤモンドCの充填率と密度を求めてみましょう。まずは、充填率を求めてみます。炭素原子の半径R cmを求めるためには、格子定数aと原子間距離rの関係を明らかにしなければなりません。図.18の立方体の対角線に注目してください。対角線の長さを原子間距離rで表すと、対角線の長さは4rとなります。ここで、対角線を斜辺とする直角三角形を考えて、原子間距離rと格子定数aとの関係を調べると、次のようになります。
![]()
![]()
次に、原子半径Rを求めます。炭素原子が互いに接していて、密に詰まっているとすると、原子半径RはR=r/2と表せます。図.18の結晶格子には、炭素原子が8個詰まっているので、ダイヤモンドCの充填率は、次のようになります。
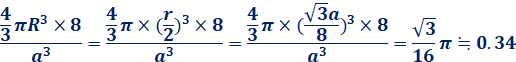
これより、ダイヤモンドCの充填率は、約34%と隙間の多い構造であることが分かります。また、ダイヤモンドCの密度は、アボガドロ定数をNA、体積をa3 cm3、原子量を12とすると、次のようになります。これに実際の格子定数a=3.57×10−8 cmを代入すると、ダイヤモンドCの密度が求まります。入試などでは、単位がcmではなくnmで与えられることが多いので、計算する際には、単位によく注意してください。
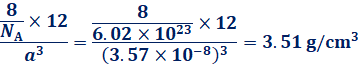
また、共有結合は非常に強い結合なので、ダイヤモンドは非常に硬いです。ただし、ここでいう「硬さ」というものは、「あるもので引っ掻いたときの傷の付きにくさ」であり、「叩いて壊れるかどうか」の堅牢さではありません。よく「ダイヤモンドは砕けない」という文句を見かけますが、それは厳密には誤りです。ダイヤモンドの割れや欠けに対する靭性は、水晶と同じ7.5であり、ルビーやサファイアの8よりも低いです。ダイヤモンドは、緩やかに加重されていく圧力に対しては高い強度を示すものの、瞬時に与えられる力に対してはそれほど強くなく、ハンマーなどで上から強く叩けば、粉々に割れてしまうこともあります。

図.19 ダイヤモンドはハンマーで叩けば砕けてしまう
このような物質の「硬さ」を評価する指標には、提唱者(ドイツの鉱物学者フリードリッヒ・モース)の名前を取った「モース硬度(Mohs hardness)」というものがよく使用されます。これは、ある物質Aで物質Bを擦ったときに、物質Bに傷が付いたかどうかによって、硬度を判定します。もし物質Bに傷が付いたら、物質Aは物質Bよりも硬いことになります。例えば、ダイヤモンドはモース硬度10で、天然にある地球上の鉱物の中では、最高クラスの硬度です。ちなみに、人間の爪のモース硬度は約2.5で、10円玉の硬度は約3.5、ガラスの硬度は約5、ヤスリの硬度は約7.5です。ダイヤモンドはその硬さから、宝石以外にも、工業的に研磨や切削など、様々な用途で使われています。
表.5 モース硬度
|
モース硬度 |
標準物質 |
用途 |
説明 |
|
1 |
滑石 |
チョーク |
黒板に字が書ける程度の脆さ |
|
2 |
石膏 |
ギプス包帯 |
人間の爪で傷が付けられる |
|
3 |
方解石 |
大理石 |
金属で擦ると容易に削れる |
|
4 |
蛍石 |
レンズ |
カッターで傷を付けられる |
|
5 |
燐灰石 |
人工骨 |
ナイフで傷を付けられる |
|
6 |
正長石 |
陶磁器 |
カッターやナイフでは傷を付けられない |
|
7 |
石英 |
水晶玉 |
ナイフで擦るとナイフの方に傷が付く |
|
8 |
トパーズ |
宝石 |
紙やすりで傷を付けられない |
|
9 |
コランダム |
宝石 |
トパーズに傷を付けられる |
|
10 |
ダイヤモンド |
宝石 |
コランダムに傷を付けられる |
現代の機械工具を作る超高度鋼は非常に硬く、これを設計図通りの精度に形作るためには、高精度の切削機が必要になります。この切削機に用いられるのが、地球上最高の硬度を誇るダイヤモンドです。ダイヤモンドなくして、現代の精密機械工作品は存在しません。また、ダイヤモンドはトンネル掘りのような、大規模土木工事にも欠かせません。巨大なトンネル掘削機のドリルに埋め込まれているのは、無数のダイヤモンドです。このダイヤモンドのお陰で、掘削機は硬い岩石や鉱石でも何でも削り、砕いて掘削することができるのです。青函トンネルができたのも、ドーバー海峡トンネルができたのも、すべてダイヤモンドのお陰です。

図.20 ダイヤモンドなくして青函トンネルは完成しなかった
ちなみに、ダイヤモンドは屈折率が高いことでも知られ、内部での全反射が起こりやすいです。ダイヤモンドのカットとしてよく用いられる「ブリリアント・カット(brilliant cut)」は、光を当ててその反射を見るとき、ダイヤモンドが最も美しく輝いて見えるように、光学的特性を数学的に考慮して、理論的に見出された形状です。白く強いきらめきや虹色の輝きは、すべてこの特別なカットがもたらすものです。ブリリアント・カットは、数学者でもあったベルギーの宝石職人であるマルセル・トルコウスキーによって1919年に開発され、標準的なものは58の面を持ちます。上部から進入した光が、すべて内部で全反射して上部から放たれ、ダイヤモンドの輝きを際立たせるような設計になっています。ブリリアント・カットは、屈折率の高いダイヤモンドに最も適した形状であり、他の宝石にはほとんど適用されることはありません。
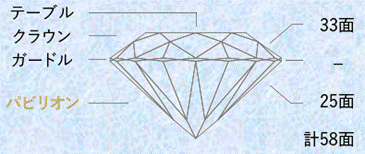
図.21 ダイヤモンドのカットは、ダイヤモンドが最も美しく見えるように計算されている
黒鉛Cも炭素の単体であり、1つの炭素原子は3つの炭素原子と共有結合で結びつき、炭素原子が正六角形の網目状に配列した平面上の巨大分子を形成しています。層中の炭素原子間の結合は共有結合ですが、重なり合った層間を結びつけているのはファンデルワールス力です。ファンデルワールス力が弱いため、黒鉛Cは軟らかくて薄片に剥がれやすいです。また、黒鉛Cは4個の価電子の内の1個の価電子が、平面上を自由電子のように動くことができるので、電気伝導性が大きいという特徴も示します。
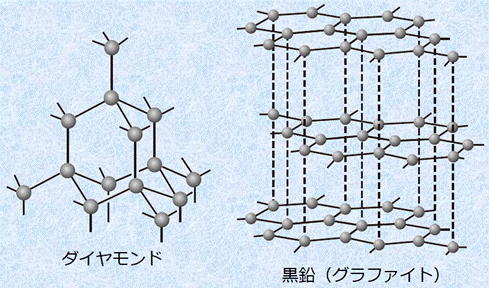
図.22 ダイヤモンドと黒鉛の結晶構造
通常のダイヤモンドとは、構造が少し異なる同素体があります。一般的には「ロンズデーライト」と呼ばれ、「六方晶ダイヤモンド」とも呼ばれます。ロンズデーライトは、ダイヤモンドと同じように、1つの炭素原子が4つの炭素原子と共有結合した構造を持ちます。自然界においては、隕石が地球に衝突した際の巨大な熱と圧力によって、隕石中の黒鉛の構造が変化して生成されます。天然のものは不純物や欠陥を含むためにモース硬度は3〜8程度ですが、純粋なものはダイヤモンドより58%硬いと予想されています。
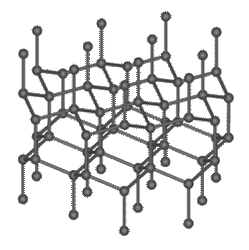
図.23 ロンズデーライトの結晶構造
(5) 結晶構造のまとめ
次の表.6に結晶構造のまとめをします。金属結晶・イオン結晶・分子結晶・共有結合結晶の特徴をよく抑えておいてください。共有結合・イオン結合・金属結合は、分子間力に比べてかなり結合力が強いです。したがって、粒子が共有結合やイオン結合で結合している結晶は、一般的に融点や沸点が高いものが多いです(常温で固体のものが多い)。金属結合で結合している金属では、遷移元素の単体は融点や沸点の高いものが多いですが、典型元素の単体は比較的低いものが多いです。
また、ファンデルワールス力のみで結合している結晶は、分子間の結合力が弱く、融点や沸点が低いものが多いです(常温で固体もしくは気体のものが多い)。また、このような分子結晶には、二酸化炭素CO2のように常圧では液体にならず、昇華するものがあります。これは、わずかに温度が上がっただけでも、分子の熱運動のエネルギーがファンデルワールス力を上回り、分子が容易に結晶から飛び出すようになるからです。
表.5 結晶構造のまとめ
|
|
金属結晶 |
イオン結晶 |
分子結晶 |
共有結合結晶 |
|
構成粒子 |
陽イオンと自由電子 |
陽イオンと陰イオン |
分子 |
原子 |
|
結合の種類 |
金属結合 |
イオン結合 |
分子間力 |
共有結合 |
|
化学式 |
組成式 |
組成式 |
分子式 |
組成式 |
|
融点 |
一般に高い |
高い |
一般に低い |
非常に高い |
|
電気伝導性 |
あり |
なし(液体や水溶液はあり) |
なし |
なし(黒鉛はあり) |
|
水への溶解性 |
不要 |
多くは可溶 |
可溶〜難溶 |
不溶 |
|
機械的性質 |
展性・延性あり |
硬くてもろい |
軟らかい |
硬い |
|
物質例 |
Fe、Cu、Na |
NaCl、MgF2、BaO |
I2、CO2、H2O |
C、Si、SiO2 |
|
構造例 |
|
|
|
|
・参考文献
1) 齊藤烈/藤嶋昭/山本隆一/他19名「化学」啓林館(2012年発行)
2) 卜部吉庸「化学の新研究」三省堂(2013年発行)
3) 石川正明「新理系の化学(上)」駿台文庫(2005年発行)
4) 斉藤勝裕「最強の「毒物」はどれだ?」技術評論社(2014年発行)
5) 左巻健男「面白くて眠れなくなる化学」PHP研究所(2012年発行)
6) 齋藤勝裕「へんな金属すごい金属」技術評論社(2009年発行)
7) 佐藤健太郎「化学で「透明人間」になれますか?」光文社新書(2014年発行)