【目次】
(i) あらゆる物体がブラックホールとなるシュバルツシルト半径
(1) 時計の歴史
(i) 時計の始まり
「時計」の始まりは、太陽の動きを利用した「日時計」のようです。日時計は、世界のどの文明にも共通に存在し、古代エジプトでは、紀元前3,500年頃から使われていたようです。日時計の仕組みですが、地面に棒のようなものを立てて、その影で時間を知るというのも、世界共通のようです。現在、アナログ式時計を始めとする回転式メーターや、つまみ式スイッチなどのほとんどが「右回り」なのも、常に日時計の影が右回りに動くことが影響しているといわれています。日時計は、1日の大まかな時間を知るには便利ですが、1分や2分など、短い時間を測定するには向いていません。これは、地球と太陽の距離や、地球の運動速度が一定でないからです。そこで、水時計や砂時計、ロウソクを利用した火時計などが作られるようになりました。

図.1 「日時計」は、影を利用して時間を知る装置である(写真は、兵庫県須磨浦山上遊園の日時計)
17世紀の半ばになると、「振り子時計」が発明されました。いよいよ機械式時計の始まりです。きっかけを作ったのは、イタリアの物理学者であるガリレオ・ガリレイでした。ガリレオは、ピサの大聖堂に行ったとき、吊るされたシャンデリアが揺れるのを見て、「同じ時間の間隔」で揺れていることに気が付きました。自分の脈拍を基準にして、振り子が揺れる時間を計ったと伝えられています。この経験を基に、ガリレオは「振り子の等時性」という理論を発表しました。そして、ガリレオの理論を基にして作られたのが、振り子時計なのです。
振り子時計は、1656年にオランダの数学者であるクリスティアーノ・ホイヘンスによって、初めて作られたとされています。クリスティアーノは、自作した望遠鏡で、土星の衛星であるタイタンを発見するなど、天文学者としても有名でした。振り子の動力として、ゼンマイやバネ、重りなどが使われていました。例えば、ゼンマイの場合は、ゼンマイを巻いて、そのあとにゆっくり戻る力を利用して、振り子を動かしていました。振り子時計は、改良を重ねながらも、発明から数世紀に渡って、「最も正確な時計」として用いられてきました。しかし、20世紀に入って、より正確な時計が発明されたことによって、徐々に衰退していきました。しかしながら、その外見上の特徴などから、今でも根強い人気があります。正確さで劣るとはいえ、きちんと調製されていれば、その誤差は、日常生活においてさほど問題にならないぐらいのものであり、現在でも愛用している人が多い時計です。

図.2 「振り子時計」は、ガリレオが発見した「振り子の等時性」を応用した時計である
ところで、時間の単位として、「分」と「秒」には、「60進数」が使われています。60進数は、メソポタミア南部の地域で繁栄した古代バビロニアが起源です。「60」という数字が、両手の指の数で表される「10」と、1年=12カ月に由来する「12」の最小公倍数であり、かつ、「2、3、4、5」の最小公倍数でもあるため、約数が多くて、割り算に便利という理由で、普及したといわれています。本当の60進数を使用するとなると、60種類の数字が必要になりますが、それでは多過ぎるため、時計の60進数は、各桁を「10進数」で表す方法で表現されています。
時計の文字盤には、「ローマ数字」が使われることもあります。ローマ数字は、ラテン文字の一部を用い、例えば、「1、2、3、4、5、6、7、8、9、10」をそれぞれ「I、II、III、IV、V、VI、VII、VIII、IX、X」のように並べて表現します。ところで、なぜローマ数字は、このような数字を用いているのでしょうか。もともと、古代ローマ人は農耕民族で、家畜のヤギやヒツジを数えるときに、木の棒に「刻み目」を入れていったそうです。柵から1匹ずつヤギが出て行く度に、刻み目を1つずつ増やしていきました。1匹目では「I」、2匹目では「II」、3匹目では「III」と表し、4匹目では3本の刻み目の右にもう1本刻み目を増やして「IIII」としました。5匹目では、4本目の刻み目の右に「V」と刻みました。このときの棒に付いた刻み目は「IIIIV」となります。6匹目では「IIIIVI」、7匹目では「IIIIVII」となります。10匹目では、「IIIIVIIII」の右に「X」という印を刻みました。このときの棒に付いた刻み目は「IIIIVIIIIX」となります。このような規則性で刻み目を増やしていくと、例えば、31匹目では「IIIIVIIIIXIIIIVIIIIXIIIIVIIIIXI」となります。このように刻んだのは、記号の1個1個が、ヤギ1匹ずつに対応していた方が便利だからです。夕方にヤギが戻ると、記号を指で端から1個1個たどっていきました。最後のヤギが戻るときに、指先が最後の記号に触れていれば、ヤギは全部無事に戻ったことになります。それ故に、ローマ数字は、刻み目のような直線を組み合わせた形をしているのです。

図.3 「ローマ数字」は、家畜のヤギやヒツジを数えるために発案された(写真はロンドンにあるビッグ・ベン)
(ii) 現代の時計
一方で、現代に使われている時計としては、「クオーツ時計」があります。20世紀後半から普及し、振り子時計に変わって、現在最も一般的な時計となっています。水晶に電気を流すと、一定の周期で規則的に振動します。クオーツ時計では、その振動数に従って、時計の歯車を動かしています。一般的なクオーツ時計の誤差は、1カ月で±20秒程度であり、特に精度の高いモデルでは、1年で数秒程度の誤差です。
そして、現代ではさらに正確な時計が発明されており、「原子時計」という時計があります。原子時計は、原子から放出される放射線の振動数を利用しています。原子そのものの振動を利用するのではなく、原子から放出される「放射線」を利用するのです。放射線の振動数は、1秒間に1,000万回で、1回の振動に要する時間は、1,000万分の1秒ということになります。これは言い換えると、1,000万分の1秒まで測定できるということです。原子時計は非常に正確であり、100万年に1秒しか狂いがないともいわれています。原子時計に基づく時刻系を「原子時」といいますが、現在の原子時の1秒は、「セシウム133原子の超微細準位遷移に対応する放射の9,192,631,770周期の継続時間」と定義されています。
また最近では、クオーツ時計と原子時計を組み合わせた「電波時計」という時計が登場しました。これは、送信局から送信される標準電波(原子時計による日付・時刻情報のデジタル信号)を受信し、自動的にクオーツ時計の誤差を修正する時計です。日本では、東京都小金井市にある独立行政法人情報通信研究機構(NICT:National Institute of Information and Communications Technology)が日本標準時を定め、この日本標準時に同期して、福島県田村市にある「おおたかどや山標準電波送信所」と佐賀県佐賀市にある「はがね山標準電波送信所」から、標準電波が送信されています。標準電波は、送信周波数40 kHzまたは60 kHzという、いわゆる長波帯に分類される電波を使用しているため、地表での伝搬は安定していますが、鉄筋ビルなどによる遮蔽や、人工的な雑音の影響を受けやすい性質を持っています。このため、標準電波が上手く受信できないと、電波時計でも時刻が狂う場合があります。最近では、太陽電池を組み込んだ電波時計も出てきており、日常生活の中で、自動的に時刻合わせと充電を行うことができる、非常に便利な電波時計も多く販売されています。

図.4 「はがね山標準電波送信所」は、日本標準時の信号を送信している(画像は国立研究開発法人情報通信研究機構提供)
(iii) 過去の時間を調べる方法
また、「放射性同位体」を利用すると、過去の時間を測ることもできます。すべての物質は、113種類以上の元素に分類できます。同じ元素であれば、原子核に存在する陽子の数は同じですが、中性子の数は異なることがあります。このように、陽子の数は同じであるものの、中性子の数が違う原子同士のことを、互いに「同位体」といいます。同位体の中には、安定なものと不安定なものがあり、不安定な同位体は、一定の確率で放射線を出して、別の元素へと変化しています。このような放射線を出す同位体が、「放射性同位体」と呼ばれるものなのです。
放射性同位体には、「半減期」というものがあります。これは、放射線を放出した結果、放射性崩壊が起こって、量が半分に減ってしまうまでの時間のことです。例えば、半減期が約7億年であるウラン235は、7億年かけて量が半分に減り、最終的には鉛207という別の元素に変わってしまいます。この年数は、物質によって決まっており、数十秒と短いものから、数十億年かかるものまで様々です。
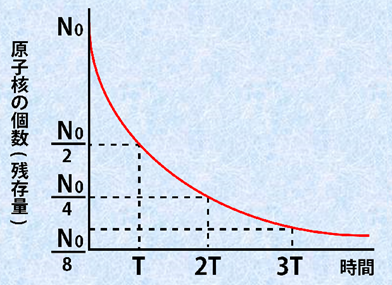
図.5 最初の原子数がN 個であるとき、その半分N /2個が放射性崩壊するまでの時間を、その放射性同位体の「半減期」という
このような放射性同位体の性質を利用して、太古の化石などが何年前のものなのかを測定する方法があります。人類が残した数万年前の遺跡などの測定には、「炭素14」という放射性同位体が活躍しています。炭素14は、大気上層で宇宙線の衝突により、窒素原子から常に作られ続けています。動植物は生きている限り、この炭素14を体内に取り込み、動植物の内部における炭素14の存在比率は、自然界の炭素14と等しくなります。しかし、生物が死滅すると、炭素14の取り込みがなくなる訳ですから、放射性崩壊を起こして、炭素14の存在比率は徐々に減っていきます。つまり、遺跡からの出土品などに取り込まれた炭素14の量を測定し、最初にあった量から、どれくらい減ったかを調べることによって、経過した時間を測定することができるのです。これは「放射性炭素年代測定法」と呼ばれ、最大で約6万年前まで測定することができます。炭素14の半減期は5,730年なので、炭素14の量がちょうど半分になっていれば、5,730年が経過したと判断できる訳です。放射性同位体による年代測定は、最初にあった量を正確に把握しなければ、正しい年代測定ができません。炭素14は、過去の太陽活動を調べることで、過去にどれぐらいの量が作られていたのか、推測することができます(放射線の科学を参照)。
![]()
過去の時間を調べる方法としては、生物のDNAの「突然変異」を調べる方法もあります。例えば、動物のミトコンドリアは、100万年に2%の割合で、DNA上の塩基配列にミスを起こすといわれています。これは、環境による影響を受けずに、一定の割合で発生すると考えられています。このような定期的な変異による分子的な違いの大きさを比較し、進化過程で種が分岐していった年代を推定するものを、「分子時計」といいます。変異の度合いが多いほど古い時代に、少ないほど新しい時代に分岐したことが示唆されます。例えば、ヒトは、約1,100〜1,300万年前にテナガザルから、約900〜1,100万年前にオランウータンから、約400〜500万年前にチンパンジーやゴリラからそれぞれ分岐したことが、分子時計から計算されています。
また、カリフォルニア大学バークレー校の研究グループは、できるだけ多くの民族を含む147人のミトコンドリアDNAを使って調査を行ったところ、全人類の起源は、すべて14万年前から29万年前のアフリカにいた女性にあることが明らかになりました。ヒトの細胞が持つミトコンドリアはすべて母親由来で、母親から受け継いだ遺伝情報を持ちます。母親は祖母から、祖母は曾祖母からミトコンドリアを受け継いでいるので、ミトコンドリアDNAを調べることで、母方の系譜について知ることができるという訳です。これにより、「ヒトはアフリカで発生して、そのあとに世界各地に進出していった」という仮説が提唱されました。この女性のことを、旧約聖書において神が創造した最初の女性「イヴ」にちなんで、「ミトコンドリア・イヴ」と呼んでいます。

図.6 「ミトコンドリア・イヴ」は、現生人類の最も近い共通女系祖先である(画像はヤン・ブリューゲルの「楽園のアダムとイヴ」)
(iv) 天文学的な時計
地球自体や宇宙にも、時計と呼べるような定期的なサイクルがあります。まず、地球についてですが、「ミランコビッチ・サイクル」と呼ばれるものがあります。この名称は、提唱者であるセルビアの地球物理学者ミルティン・ミランコビッチの名前にちなんでいます。ミランコビッチ・サイクルは、地球の軌道要素の天体力学的な変動――地球の公転運動のズレ、自転軸と公転面との角度の変化、自転軸の歳差運動――によって、「日射量」が変動する周期のことです。地球は、太陽の周囲を公転していますが、完全な円軌道ではなく、わずかに歪んだ楕円軌道を描いています。その軌道は、仮に地球が太陽系で唯一の惑星ならば、未来永劫変わることはありません。ところが、実際には木星などの重力の影響を受けるため、若干のズレが生じるのです。
地球の軌道は、だいたい10万年ぐらいのサイクルで、円軌道に近付いたり歪んだ楕円軌道になったりして、公転運動のズレを発生させています。また、軌道面の垂線に対する自転軸の傾きは、現在では23.45°です。これも周期的に変動することが知られており、だいたい4万年ぐらいのサイクルで、22.1〜24.5°の間を揺れ動いているのです。そして、地球の自転軸の方向は、円を描くように変化します。これは、コマを回したときにその回転が弱まってくると、コマの芯が左右に揺れ動くのと同じ現象で、「歳差運動」といいます。この現象が、地球にも2万年ぐらいのサイクルで起こっているのです。これらの変化は、地球が受け取る日射量に大きな影響をもたらすので、10万年周期で訪れている氷期との関連性も指摘されています(地球温暖化の科学を参照)。

図.7 「ミランコビッチ・サイクル」による日射量変動が、氷期と間氷期サイクルの原因であると考えられている
宇宙に関しては、「パルサー」という星の発する電波が、規則正しいということで有名です。パルサーは、太陽の数倍の質量がある恒星の超新星爆発によって、その中心部分が圧縮されてできた天体です。非常に強い重力のため、原子核に電子が吸収されて、星のほとんどが中性子からなっています。大変密度が高いことが特徴で、半径10 kmぐらいの大きさに、太陽ぐらいの質量を持つほどです。そして驚くべきことは、パルサーの発する電波の規則正しさです。「宇宙の灯台」という異名があるほどで、100万年に1秒も狂わない正確さといわれています。これは、原子時計に匹敵する精度なのです。パルサーからの電波を受信した当初は、電波の周期が自然由来のものとは思えないほど規則的だったため、「宇宙人からの信号に違いない」と騒がれるほどでした。
パルサーが正確な周期で電波を発する理由として、星自体が巨大な棒磁石になっていて、高速で正確に自転しているからではないかと考えられています。電波の周期は、自転の周期とほぼ一致しています。有名な「かに星雲」は、今から950年ほど前に現れた超新星爆発の残骸であり、その中心には、1秒間に30回転もするパルサーが存在しています。銀河系では、これまでに1,700個以上のパルサーが発見されています。電波を発するパルサーは、自転の速度が徐々に遅くなり、1,000万年ほど経つと、電波を発しなくなるといわれています。
(2) 生物が持つ時計
(i) 生物の体内時計
生物は、生まれつき自分の体内に体内時計を持っていて、それは「サーカディアン・リズム(概日周期)」と呼ばれています。1938年にアメリカの生理学者であるナサニエル・クライトマンは、マンモス・ケーブ国立公園にある地下40 mの洞窟の中で、32日間を過ごしました。クライトマンは、人間の睡眠と覚醒のリズムは単なる「習慣」に過ぎないのか、それとも人間には固有の変化しにくい「体内時計」が備わっているのかを、実験によって確かめようとしたのです。すると、クライトマンは時計がないのにも関わらず、だいたい25時間の周期で生活していたといいます。生活のリズムは、1日当たり1時間ずつ遅れていったようですが、人間の体内時計は、地球の自転の周期と同じで、おおよそ24時間ということができるでしょう。
なお、通常は日照の有無による昼と夜があるので、その光刺激を用いて、人間は体内時計のズレを補正していると考えられています。クライトマンが行った実験より、人間には体内時計が備わっており、人間の睡眠リズムを2倍に伸ばしたり、半分に縮めたりすることはできないということが分かりました。そして、この研究は、宇宙船の中の環境設計に大きな影響を与えました。宇宙船の中に明暗サイクルを模擬した環境を作ることで、宇宙飛行士の健康を維持できるようになったのです。

図.8 かさ上げしたベッドの長い脚は、クマネズミが登れないよう、バケツの中に入れられている
体内時計は、「ホメオスタシス」の一種であると考えられています。ホメオスタシスは、生体内部や外部環境の変化に関わらず、生体の状態を一定に保とうとする機能のことです。これによって、体温や血圧、脈拍、ホルモンの分泌量などは一定の状態に保たれ、生命を維持できるようになります。体内時計も、睡眠の周期や行動などに大きな影響を及ぼしており、生命の維持には欠かせないものです。
それでは、体のどこに体内時計があるのかというと、脳の視床下部の「視交叉上核」という場所です。動物実験でラットの視交叉上核を破壊すると、合計の睡眠時間はあまり変わらないものの、一回の睡眠の長さとタイミングが、完全にバラバラになってしまうことが知られています。視交叉上核は、光の情報を目から受け取りとり、他の情報と統合して、脳内の「松果体」という場所へ信号を送信します。そして、夜に暗くなって網膜に入る光が減ってくると、「メラトニン」という睡眠ホルモンが、松果体から分泌されます。メラトニンが分泌されることによって、体温や血圧などが低下して、睡眠の準備ができたと体が認識し、眠気を感じるようになるのです。また、朝日を浴びて規則正しく生活することで、メラトニンの分泌される時間や量が調整され、人の持つ体内時計の機能や生体リズムが調整されます。そのため、不規則な生活や昼間に太陽を浴びないような生活を続けると、メラトニンが上手く分泌されなくなり、不眠症などの睡眠障害の原因となります。

図.9 「体内時計」は意識に上ることはないが、睡眠の周期や行動などに大きな影響を及ぼしている
また、ある実験によると、人間が感知できる最短の時間は、0.03秒という結果が示されました。どんなに頑張っても、これより短い時間は感知できない訳です。それでは、人間が感知できる最長の時間は、どれぐらいでしょうか?実は、たったの3秒ほどでしかないのです。そんな馬鹿なと思うかもしれませんが、実験によって判明したことです。人間は、3秒ごとに時間を感知し、その記憶を脳内でつなぎとめているのです。この3秒というのは、年齢を重ねるとだんだん伸びてきて、5秒ぐらいになるそうです。年齢を重ねるにしたがって、時間が経つのが早いと感じる人は多いと思いますが、若者と老人では、このように時間を感知する長さが違っているようなのです。「3秒ごとに情報が増える状態」と、「5秒ごとに情報が増える状態」とでは、3秒ごとの方が、脳内に蓄積される情報量が多いのは明白です。刺激が無くなり、単調な毎日を過ごすと、時間の経過を早く感じるようで、刺激を沢山受けた方が、時間が長く感じられると考えられています。

図.10 老人と若者では、時間の感じ方が異なると考えられている
(ii) 細胞が持つ時計
私たちの細胞には、「ヘイフリック限界」と呼ばれる細胞の分裂回数の限界が、あらかじめ決められています。例えば、ヒトなどの動物組織から取り出した細胞を培養すると、一定数の分裂を行うと細胞周期が停止して、それ以上は分裂できない「細胞老化」と呼ばれる状態になります。細胞が分裂できる回数は生物種ごとに異なりますが、ヒトでは約50回ほどです。そして、その分裂回数をカウントしているのが、「テロメア」という遺伝子なのです。テロメアは、染色体の末端に輪のような形で存在し、遺伝子の恒常性の維持に関与していると考えられています。細胞が複製されると、染色体も複製されますが、新しく複製された染色体のテロメアは、末端の塩基部分が複製されないために、元の長さよりも短縮してしまいます。細胞分裂が繰り返され、テロメアがどんどん短縮していくと、テロメアは輪を作れなくなり、このことを細胞自身が染色体に傷害があると認識し、細胞分裂はそこで停止することになります。まさにテロメアは、燃え尽きると寿命が無くなる「命のロウソク」のような役割なのです。
実際に、76歳男性とその孫にあたる27歳男性のテロメアを調査したところ、76歳男性で76%、27歳男性で40%のテロメアが減少していたといいます。テロメアの長さから考えられる最長の寿命は約120年とされており、この年数は世界一の長寿者であるフランス人女性ジャンヌ・ルイーズ・カルマン(1875年2月21日〜1997年8月4日)の122年とほぼ一致しています。テロメアが短縮すると、細胞分裂の間隔が伸びていき、染色体内の遺伝子の不安定性を増長させることから、老化の原因として挙げられることが多いです。ただし、老化の原因は無数にあるため、テロメアだけが老化の原因という訳ではありません。
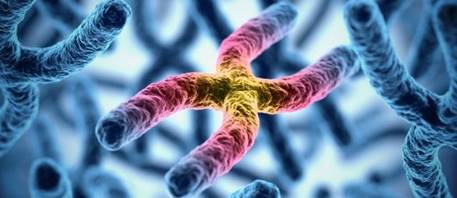
図.11 「テロメア」は、染色体の末端に輪のような形で存在する
また、「クローン技術」で生まれたヒツジの細胞では、正常の繁殖で生まれた同年齢のヒツジより、テロメアの長さが短縮されていたことが確認されています。スコットランドのロスリン研究所で誕生した、世界初の哺乳類の体細胞クローンであるドリーは、遺伝情報の元が6歳の成ヒツジ体細胞だったので、誕生時に遺伝子がすでに6歳程度であったのではないかという推測がされています。クローン技術により誕生したドリーは、6歳になったときに進行性の肺疾患になり、回復が見込めないことから安楽死させられましたが、5歳頃から、高齢のヒツジに特徴的な関節炎を発症して、衰弱していたそうです。誕生時に遺伝子が6歳であったと仮定すると、死亡したのが12歳となります。ヒツジの寿命が10〜12年ほどであることを考えると、死亡時にはかなりの老齢になっていたということでしょうか。ここから、「クローン技術は不完全で命が短くなる」といった可能性が指摘され、倫理面以外からの規制論を後押しする大きな根拠となりました。
しかし、最近では、「クローン動物にテロメア短縮は見られない」という論文も多く発表されています。2016年にノッティンガム大学の発生生物学者であるケビン・シンクレアは、「クローンであることと寿命が短いことの間には関係性はない」という研究結果を公表したのです。研究チームは、13頭のクローン羊を飼育し、老齢になるまで一連の試験を行うことで、クローン羊は単に健康なだけでなく、完全に通常のヒツジと同じように老化していくということを明らかにしています。

図.12 「クローン技術」により誕生したドリーの剥製(画像は国立スコットランド博物館で撮影)
テロメアは、人間だけでなく他の生物にも存在しますが、テロメアが存在しない生物もあります。例えば、大腸菌などの単細胞生物には、テロメアがありません。よって、大腸菌は無限の分裂能を持ち、何回でも細胞分裂が可能なのです。ということは、人間もテロメアがなければ、何回でも細胞分裂が可能になり、永遠の命を手に入れることができるようになるのでしょうか?しかし、テロメアが存在せずに、細胞が無秩序に分裂してしまうと、ガンのような「悪性腫瘍」が、体内のあちこちにできてしまいます。多くのガン組織では、テロメアを伸長させる「テロメラーゼ」という酵素が発現しており、細胞分裂回数が著しく増加していることが分かっています。
1951年に子宮頸ガンで亡くなった30代の黒人女性ヘンリエッタ・ラックスの腫瘍病変から採取された「HeLa細胞」は、細胞の提供者である女性が亡くなったあとも、ずっとフラスコの中で生き続けています。未だに繁殖力旺盛で、若干劣悪な環境でも増殖を続け、彼女は世界中の研究室で断片として生きています。これまでに培養されたHeLa細胞は、推定で5,000万tを超えるといわれています。この量は、日本が海外から1年間に輸入する全食料に匹敵します。とはいえ、「彼女」を示す唯一の印である遺伝子自体が、ガン化した影響で滅茶苦茶になっており、もはや元の遺伝子の性質を維持してはいません。ここからも、私たちの寿命は、無限ではないといえます。ただし、テロメラーゼを上手く使うことができれば、ある程度の寿命延長は可能になるかもしれません。
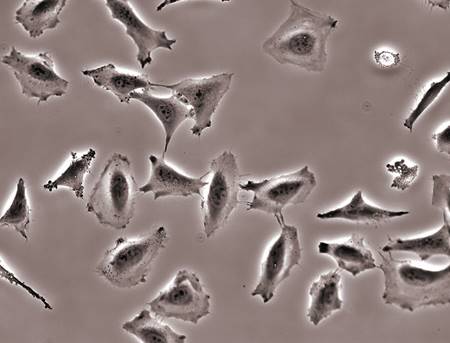
図.13 「HeLa細胞」のゲノム配列が解読されたが、中身はガンの影響でエラーだらけだった
(iii) ゾウとネズミの生物学的時間
ハツカネズミの寿命は、だいたい2〜3年です。それに対して、ゾウの寿命は、だいたい80〜100年といわれています。これだと、寿命が短いハツカネズミは、人生を謳歌する時間が短く、寿命の長いゾウは、有り余るほどの時間を与えられたことになります。何だか、不公平な感じがしますね。しかし、それは両者が公平になるように、微妙にバランスが取られています。様々な哺乳類で、体重と時間とを測ってみると、時間は体重の1/4乗に比例することが分かっているのです。
![]()
つまり、ゾウのように体重が大きな動物ほど、何をするにも時間がかかるということです。動物が違うと、時間の流れる速度が変わってきます。例えば、体重が10倍になると、時間は101/4=1.8倍になります。時間が倍近くかかるのですから、これは動物にとっては無視できない問題です。この「1/4乗則」は、時間が関わっている様々な現象に広く当てはまります。例えば、動物の一生に関わるものでは、「寿命」を始めとして、「大人のサイズに成長するまでの時間」、「性的に成熟するのに要する時間」、「赤ん坊が母親の胎内に留まっている時間」など、すべてがこの「1/4乗則」に従います。日常の活動の時間も、やはり体重の1/4乗に比例します。「息をする時間間隔」、「心臓の鼓動間隔」、「腸が蠕動する時間」、「血液が循環する時間」、「生体異物を除去するのに要する時間」、「タンパク質が合成されてから壊されるまでの時間」など、枚挙に暇がありません。
時間に関係のある現象が、すべて体重の1/4乗に比例するのなら、時間に関係するものを組み合わせて割算をすると、体重によらない数が出てきます。例えば、「息を吸って吐いて、吸って吐いて」という繰り返しの間隔の時間を、心臓の鼓動の間隔時間で割ってやると、「息を一回吸って吐く間に心臓は4回鼓動する」ということが分かります。これは、哺乳類ならサイズによらず、すべての哺乳類に当てはまります。次に、寿命を心臓の鼓動時間で割ってみます。そうすると、哺乳類ではどの動物でも、「一生の間に心臓は20億回鼓動する」ということが分かります。さらに、寿命を呼吸する時間で割れば、「一生の間に5億回だけ息を吸って吐く」ということが分かります。これも、哺乳類ならサイズによらず、ほぼ同じ値となります。

図.14 ゾウの寿命は、だいたい80〜100歳で、20歳ほどで成獣になる
物理的な時間で測れば、ゾウはハツカネズミよりずっと長生きです。ハツカネズミは2〜3年しか生きませんが、ゾウは80〜100年の寿命を持ちます。しかし、心臓の拍動を「時計」として考えるならば、ゾウもハツカネズミも全く同じ長さだけ生きて、寿命を迎えることになります。ハツカネズミは1回の鼓動が0.1秒間隔なのに対し、ゾウは1回の鼓動が3秒間隔です。「ハツカネズミが感じる0.1秒が、ゾウが感じる3秒に相当する」と仮定したら、「ハツカネズミの1日は、ゾウの30日分に相当する」訳です。もちろん、このような時間の間隔を、直接ハツカネズミやゾウに聞いて確かめる訳にはいきませんから、これは飽くまで推測ということになります。しかしながら、ハツカネズミのような小さい動物では、体内で起こるすべての現象の時間が速いのですから、「一生を生き切った感覚」で考えると、存外ゾウもハツカネズミも変わらないのではないでしょうか?
私たちは、普通は「時計」を使って時間を測ります。あの歯車と振子の組み合わさった機械が、コチコチと時を刻み出し、時が万物を平等に非常に駆り立てていくと、私たちは考えています。ところが、そうでもないらしいです。ゾウには「ゾウの時間」、イヌには「イヌの時間」、ネコには「ネコの時間」、そしてネズミには「ネズミの時間」と、それぞれのサイズに応じて、違う時間の単位があることを、生物学は教えてくれます。生物におけるこのような時間を、物理学的な時間と区別して、「生物学的時間」と呼んでいます。
(3) 時間が科学された始まり
(i) アリストテレスの考えた時間
「時間とは何か。誰も私に聞かないときは、よく知っている。しかし、誰かに説明しようとすると、何も分からなくなる」――これは、古代キリスト教の哲学者アウレリウス・アウグスティヌスの言葉です。確かに、誰でも時間に関する直感的洞察は持っているけれども、「時間とは何か」と改まって聞かれると、答えに詰まってしまうものです。「時間」を科学的に考え始めたのは、古代ギリシアが始まりです。この時代では、「科学」と「哲学」の違いは、ほとんどありませんでした。「自然を考える」ことも、「人間を考える」ことも、すべて哲学者の仕事だったからです。そして、古代ギリシアには、偉大な哲学者であるソクラテスがいました。時の権力者から疎まれ、遂には裁判にかけられて、死刑を宣告されてしまうのは、皆さんもご存知のことと思います。そのソクラテスの弟子にプラトンがいますが、プラトンは時間について、科学的な考察を残しました。プラトンは、天体の星の運行が周期的であることに着目し、時間も周期的であると考えました。人間は、「時間」という永遠の周期の中で生きているという考察です。

図.15 プラトンは、古代ギリシアを代表する哲学者である
プラトンの弟子のアリストテレスは、プラトン主催のアカデメイアで学び、後にマケドニアの王であるアレクサンドロス大王の家庭教師になった人です。そのアリストテレスの時間についての考察は、師匠のプラトンとは異なるものでした。時間は、物体の運動を計る「道具」に過ぎない――つまり、「時間は物体の運動を数量化したものである」というのです。例えば、物体がA地点からB地点に移動したとすると、「物体がA地点からB地点に移動したことを人間が認識するため」に、時間という概念が存在するともいえるのです。この考えは、時間を絶対的なものとして捉えない、現代の物理学にも通じるものがあるといえそうです。アリストテレスの考えは、長い間、ヨーロッパでは規範とされてきました。
アリストテレスは、このように現代の科学の礎を築いたのですが、それが皮肉にも、科学の発展を阻害した面もあるのです。例えば、アリストテレスは、「太陽は地球の周りを回っている(天動説)」と主張したり、「物体は重いものほど速く落下する」と主張したりしました。中世のヨーロッパは、教会が絶大な権力を握っていました。教会がアリストテレスの考えを支持していたので、これに反対することは、当時では絶対に許されませんでした。特に「天動説」は、イエス・キリストの教えに近いということで、これを否定すれば、命さえも危うくなったのです。

図.16 アリストテレスは、西洋最大の哲学者の一人とされ、その多岐に渡る自然研究の業績から「万学の祖」とも呼ばれる
(ii) ガリレオの考えた時間
イタリアの物理学者であるガリレオ・ガリレイは、イタリアのピサの斜塔から、重さの違う2つの金属球を同時に落としました。それが重さに関係なく同時に地面に落下することを証明し、アリストテレスが間違っていることを示しました(なお、この有名な実験は、ガリレオの弟子であるヴィンチェンツォ・ヴィヴィアーニの創作で、実際には行われていないとする説もあります)。またそれだけでなく、アリストテレスの「天動説」を否定して、太陽を中心とし、地球がその周りを回っているというコペルニクスの「地動説」を支持したために、宗教裁判にかけられ、地動説を撤回したという有名なエピソードもあります。
ガリレオは数々の歴史的な発見をしましたが、その中でも、特に「ガリレイの相対性原理」は、後世に大きな影響を与えました。これは、運動している物体の内部でも、静止しているときと同じように、物体の運動の法則が働くというものです。例えば、ボールを上に放り投げると、真下に落下します。そして、電車に乗ってボールを上に放り投げても、同様に真下に落下します。天動説が信じられていた当初は、「もし仮に、地球が自転しているとしたら、鳥は地球の自転の速さに追い付けず、前に飛ぶのではなく後ろに下がってしまうだろう」といわれていました。それ故に、天動説は、地球は静止しているという根拠になっていたのです。しかし、ガリレイの相対性原理によれば、動いている地球と一緒に空を飛ぶ鳥も動くので、自転している地球でも、静止しているときと同じように運動の法則が働くという説明ができたのです。動く電車の中でのボール投げと同じです。ガリレイの相対性原理の「運動の法則」の部分は、後にドイツの物理学者であるアルベルト・アインシュタインによって、電磁気学を含めた「物理法則」に拡張され、特殊相対性理論へと発展することになります。

図.17 「天動説」では、地球は宇宙の中心にあって静止しており、すべての天体が地球の周りを公転していると考える
(iii) ニュートンの考えた時間
ガリレオが亡くなった年である1643年にイギリスに生まれたアイザック・ニュートンは、数多くの偉大な業績を残したことで知られる物理学者です。ニュートンは、すべての物質は互いに引力を及ぼし合っているという「万有引力の法則」を発見したことでも有名ですが、「慣性の法則」という大事な法則も考え出しました。これは、ガリレオの理論を法則としてまとめ上げたものです。言葉で表現すれば、次のようになります。
「運動している物体は、外から力を加えられない限り、等速直線運動を続ける」
例えば、地球上でボールを床に転がしてみると、しばらくすると運動は止まってしまいます。これは、摩擦という外からの力によって、運動するエネルギーが奪われてしまったからです。空気との摩擦もない宇宙空間でボールを投げると、ボールは同じ速度を保ったまま、永遠に運動を続けることになるのです。人工衛星が一度大気圏を出ると、何も動力を加えなくても、そのまま進んでいくのと同じことです。
ここで、ニュートンの時間に関する考えですが、古典力学の基礎を築いた自身の著作「プリンキピア」の中で、こんなことを述べています。「時間は絶対的なもので、運動が加速したり減速したりできるのとは対照的に、時間の流れは速くなったり遅くなったりすることはない」というのです。また、空間に対しても、「空間は伸び縮みするようなことはなく、静止しているもの」と、時間と同じようなことをいっています。ニュートンは、空間は「物理現象が起きる単なる入れ物」で、時間は「それとは独立した宇宙のどこでも一様に刻まれるもの」と考えたのです。
また、現代の物理学では、「重力が伝わる速度は光の速度と同じ」と考えられていますが、ニュートンは、「2つの物質の間で重力が作用するとき、時間はかからず、瞬時に伝わる」と考えていました。つまり、重力の伝わる速度は、無限大であると考えていた訳です。ニュートンのこの考えは、後にアインシュタインによって否定されますが、全くのでたらめということではありません。地球上で生活する私たちは、時間や空間が大きく伸び縮みするような現象に遭遇することは、まずありません。地球上で生活する限り、ニュートンの考えは正しいのです。宇宙でも、重力や速度があまり大きくない場合には、ニュートンの考えは成立します。しかし、重力が大きい恒星やブラックホール、光の速度に近付いたときなど、かなり壮大なスケールになると、時間や空間が伸び縮みするような現象が発生するのです。現代の物理学の視点では、「ニュートンの考えは、重力や速度があまり大きくない場合の相対性理論の近似である」と理解されています。

図.18 ニュートンの「プリンキピア」は、古典力学の基礎を築いた画期的な著作で、近代科学における最も重要な著作ともいわれる
(iv) ガリレイ変換とローレンツ変換
速度は、距離を時間で割ることで求められるように、時間と密接な関係にあります。そして、速度というものは、足し算や引き算で大きさが変わることがあるのです。例えば、時速100 kmで走る列車の中で、野球の投手が列車の進行方向に向かって、時速100 kmのボールを投げると、列車内の乗客には、ボールの速度は時速100 kmにしか見えません。しかし、ホームで列車の通過を見ている人には、ボールは時速200 kmに見えるのです。つまり、列車の速度100 km/hとボールの速度100 km/hが、足し算されたことになります。
100 km/h + 100 km/h = 200 km/h
また、時速100 kmで走行する列車の横を、時速100 kmで並走する自動車があるとして、自動車から列車を見ると、静止しているように見えます。これは、列車の速度100 km/hから、自動車の速度100 km/hを引き算したことになります。投手が投げたボールは、時速100 kmで同じでも、それを列車の中で見る人と、ホームで見る人では、速度が違って見えるのです。
100 km/h − 100 km/h = 0 km/h
つまり、列車に乗って動いている人と、ホームで静止している人では、「慣性系」が違うという訳です。このような現象は、時間が伸び縮みせず、常に一定であるので成立することです。列車内の人は、ボールが時速100 kmで進む距離(空間)だけが関係しているのに対し、ホームにいる人は、ボールが時速100 kmで進む距離(空間)の他、列車が時速100 kmで進む距離(空間)が関係しています。それ故に、ホームにいる人は、列車内にいる人と同じ時間であるにも関わらず、列車内の人より距離(空間)が2倍に増えたため、時速200 kmに見えるのです。速度を求める式を見れば分かりますが、分母の時間が同じで、分子の距離が2倍になれば、速度も2倍になるのです。これは「ガリレイ変換」と呼ばれるもので、「ある慣性系」における物理現象の記述を、「別の慣性系」での記述に変換するための方法です。地球上における物理現象のように、重力や速度があまり大きくない場合には、「ガリレイ変換」が成立するのです。
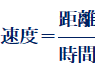
ところが、ガリレイ変換の理屈だと、ある疑問が生じてきます。速度の上限を光の速さまでと考えた場合、光と並行して、光と同じ速度で追いかければ、光は止まって見える――つまり、光の速度はゼロになるのではないかということです。結論を述べますと、現代の物理学では、光を同じ速度で追いかけても、光は光の速さ(秒速30万km)にしかなりません。どんな状況にあっても、光の速さは常に一定なのです。これを「光速度不変の原理」といいます。私たちの日常生活では、近似的にガリレイ変換が成り立ちますが、速度が光速の10%以上にまで近付いたときは、ガリレイ変換が成り立たず、実際の観測結果とのズレが大きくなります。そこで、ガリレイ変換に修正を加えた「ローレンツ変換」が登場します。
もともと、ローレンツ変換とは、1887年の「マイケルソン・モーレーの実験」という、光の速度に関する実験を証明するために考え出された理論です。この実験は、後に「最も成功した失敗実験」として、科学の歴史にその名が刻まれることになります。地球は東西方向に自転や公転をしており、静止系ではないので、東西や南北で測定される光の速度は、それぞれで異なるはずです。マイケルソンとモーレーは、高精度の干渉屈折計を使って、運動する観測者によって、光の速度が違うということを確かめようとしたのです。しかし、実際の結果は、その予想を裏切るものとなりました。観測者が光に向かって運動しても、光から遠ざかって運動しても、光の速さは同じになるという結果が導かれたのです。これは、光の速さが観測者の状態によらず、常に一定であることを意味します。当時の物理学者たちは、自分たちの考えていた常識とは違う現実に、狐につつまれたような気がしました。そんな実験の矛盾を解決するために、オランダの物理学者であるヘンドリック・ローレンツは、次のような仮説を提唱しました。
「物体が運動するとき、運動する方向に対して、物体の長さが短縮する」
この現象は、「ローレンツ収縮」とも呼ばれています。そして、この仮説を基に導かれたのが、「ローレンツ変換」という複雑な式なのです。ローレンツ変換は、当時信じられていた「エーテル理論」に基づくものです。19世紀の物理学者たちは、光は音と同じような「波」であるから、音が空気の振動で伝わるように、光も何かの振動で伝わるに違いないと考えていました。そして、アリストテレスが「天を満たしている元素はエーテルである」といったのにちなんで、その未知の媒質に、物理学者たちは「エーテル」という名を付けていました。エーテルは目に見えず、宇宙全体に充満している質量を持たない媒体で、光以外の何からも影響を受けないと考えられていました。「周期表」を初めて作成したことで有名なロシアの化学者メンデレーエフは、エーテルに「原子番号0」を与えていました。マイケルソン・モーレーの実験から、光は真空を通って伝播することが分かり、エーテルは実際には存在しない媒体であることが分かりました。
マイケルソン・モーレーの実験から24年経過した1905年、ベルンで特許庁三級技術専門審査官として働いていた、当時全くの無名だった26歳のアインシュタインは、「光速が不変である意味」を解明しました。エーテル理論と共に、ニュートンの時代から考えられていた「時間は絶対的である」という概念は、アインシュタインによって否定されることになります。実のところ、マイケルソン・モーレーの実験を解釈するためには、単なるローレンツ収縮だけでは足らず、時間に関する「大胆な理論」が必要だったのですが、それがアインシュタインの「特殊相対性理論」であった訳です。
(4) 相対性理論とは何か?
(i) アインシュタインの発見
「時間」は、誰に対しても平等にあるものではありません。また、常に同じように進むものでもありません。観測者の状況によって、遅くなったり早くなったりします。時間そのものが、長くなったり短くなったりするのです。そのことを発見したのは、ドイツの物理学者であるアルベルト・アインシュタインでした。アインシュタインが1905年に発表した「特殊相対性理論」と1915年に発表した「一般相対性理論」では、それまで信じられてきた時間や空間の概念が覆されました。
当時は、時間や空間の尺度は伸びたり縮んだりしない、絶対不変のものだと信じられていました。しかし、アインシュタインは、それに異論を唱えました。アインシュタインは、時間や空間の尺度は観測者の状況によってそれぞれ違う――つまり、時間や空間は相対的なものである――と結論付けたのです。これが「相対性理論」という名の意味するところです。まず「特殊相対性理論」では、次の結論を導き出しました。
「時間は、速い速度で運動する物体では、進み方が遅くなる」
特殊相対性理論は、「重力の影響がないとき、観測者がどんなに速いスピードで運動していても、物理法則は等しく観測者に及ぶ」という理論です。また、「光の速度は常に一定で、宇宙の中で絶対的である」と定義しています。光の速度を基準にして、時間が伸びたり縮んだりするのです。特殊相対性理論によると、ある速度で動いている観測者の時計の進み方は、静止している観測者の時計よりも進み方が遅くなることが予言され、これは実験でも確認されています。続いて、「一般相対性理論」では、次のことを指摘しました。
「時間は、重力が大きいところでは、進み方が遅くなる」
一般相対性理論も、「観測者がどのような運動をしていても、物理法則は等しく観測者に及ぶ」という考えに基づいています。ただし、こちらは重力の影響があることを前提にしています。そして、アインシュタインは、「加速度と重力は区別できない」と考えていました。これを「アインシュタインの等価原理」といいます。例えば、あなたが宇宙船に乗っているとしましょう。加速度を計測できる加速度計は、原理的には、ばねに重りが付いたものでしかありません。ばねが伸びたり縮んだりすると、加速度がかかっていることが分かるのです。しかし、このときにもしかしたら、宇宙船は加速していたのではなく、どこかの星の重力場にさしかかっただけなのかもしれません。宇宙船が加速しても、重力が強くなっても、加速度計の中に入っているばねは、同じように伸びるのです。つまり、物理学的な測定器では、力が原因の加速度なのか重力なのかは、全く区別が付かないという訳です。特殊相対性理論と一般相対性理論は、何だか全く違う理論のように思えますが、根本的には似たような理論なのです。
(ii) 相対性理論による身近な時間の遅れ
ということで、加速度がかかっている状態、すなわち重力の影響がある状態を扱うことができる一般相対性理論は、ときに「アインシュタインの重力場理論」と呼ばれることがあります。そして、アインシュタインは、「重力は時間や空間の歪みである」と説明しています。一般相対性理論では、強い重力場にいる観測者は、それよりも弱い重力場にいる観測者よりも、時計の進み方が遅くなります。例えば、地球では、標高が高いところよりも低いところの方が、地球の中心との距離が近くなるので、重力が大きいです。そのため、標高が10 cm低くなると、1秒間に10−17秒ほど時間がゆっくりと流れます。これを利用することで、現在では5 cmの精度の標高差測定が可能になっています。また、頭の先と足の先では、足の先の方が10年間で1億分の4秒だけ時間が遅れます。しかし、この時間の変化はあまりにも小さすぎるために、私たちが地球上にいる限り、時間が早くなったり遅くなったりするのは、ほとんど実感することはありません。宇宙空間に出て、質量が太陽の何十倍もある巨大な恒星やブラックホールに近付いたときなど、かなり壮大なスケールになって初めて、時間は伸びたり縮んだりすることが実感できるのです。
また、特殊相対性理論によると、時間は、速い速度で運動する物体では遅くなります。これは、地球上で、次のような実験を行うことで実証されています。例えば、2機のジェット機に正確な時計を積んで、1機は東の方角に、もう1機は西の方角に飛び立ったとします。そして、それぞれのジェット機が、同じ速度で赤道上を1周して同じ場所に戻ってくると、各ジェット機の時計に、ほんのわずかなズレが発生します。東の方角に飛んだジェット機が、西の方角に飛んだジェット機よりも、時間がほんの少し遅れたのです。

図.19 ジェット機を使った実験で、地球上でも「特殊相対性理論」を確かめることができる
ここで、1つ疑問が生じます。2機のジェット機は、同じ速度で飛行したのに、なぜ時間の進み具合が違ったのでしょうか。これは、宇宙から見ると地球が東に向かって自転しており、東の方角に飛んだジェット機は、ジェット機の速度に、地球の自転の速度が加わったからです。そのため、東の方角に飛んだジェット機は、西の方角に飛んだジェット機よりも、時速1,700 kmほど早くなります。その分、西の方角に飛んだジェット機よりも、時間の進み具合が遅れたと考えられます。ただし、時間が遅れるといっても、ジェット機の速度では、1秒につき1兆分の1秒ぐらいの遅れなので、正確な計測機器がない限り、私たちには実感できないでしょう。時速1,000 kmで飛行するジェット機のパイロットは、1秒当たり約1兆分の1秒だけ時間が遅れるので、長時間ジェット機に乗っていると、寿命が少し長くなると考えられます。仮に80年間、空中給油などでジェット機を飛ばし続けたとして、このときの時間の遅れを計算してみましょう。1年=31,536,000秒とすると、
![]()
つまり、80年間ジェット機に乗り続けても、1秒も寿命が延びないということになります。身近なところでは、新幹線が速い乗り物ということになりますが、時速300 km程度の速さでは、さらに時間の遅れは少ないことになります。たとえ、あなたが一生新幹線に乗っていたとしても、寿命は1秒たりとも延びません。ただし、乗り物の速さがかなり速い場合は、少し事象が違ってきます。運動する物体が光の速度(秒速30万km)に近付いていくと、時間の遅れは顕著になっていきます。速度の上限は光速なので、光速に近い速度で運動する物体は、ほとんど時間の進みがないことになります。しかし、現在の科学技術力では、この速さは実現不可能です。光速に近付くほど、運動する物体の質量は無限大に近付き、それ以上速度を上げることが難しくなっていくからです。速度の大きいスペースシャトルでさえ、光速の1%にも満たないのです。
ところで、地球ができたばかりの太古は、地球の自転の速度が、現在よりもずっと速かったと考えられています。地球が誕生した46億年ぐらい前は、1日の長さは5時間程度でした。6億年ぐらい前でも、1日の長さは22時間程度で、今よりも速く自転していました。潮汐によって移動する海水と海底との摩擦、大気と地面との摩擦などによって、地球の自転速度は、徐々に遅くなっているのです。計算によると、1日の長さは、100年につき1,000分の1秒ほど長くなっているといいます。ということは、大昔では1日の長さは短いけれども、時間の進み方は現代よりゆっくりだったといえそうです。地球の自転の速度が遅くなった現代では、時間がほんのわずか早く進んでいるようです。
(5) 伸び縮みする空間と特殊相対性理論
特殊相対性理論は、「重力の影響がないとき、観測者がどんなに速いスピードで運動していても、物法則は等しく観測者に及ぶ」という理論です。特殊相対性理論は、一般相対性理論よりも影響が強いです。そして、運動する物体において、時間が伸びたり縮んだりするのは、「光の速度」と大きな関係があります。特殊相対性理論では、「光の速度は常に一定で、宇宙の中で絶対的である」と定義されています。つまり、光の速度に合わせて、「時間」が伸びたり縮んだりしているのです。ここで、速度を求める式を思い出してください。
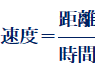
速度は、「距離」を「時間」で割ることで求めることができます。例えば、「距離」が増えた場合では、速度を一定にするには、「時間」も増やさないといけません。逆に「距離」が減った場合では、「時間」も減らさないと速度は一定になりません。速度を一定に保つために、「時間」が伸び縮みするのです。さらに、ここで大事なことは、「時間」だけでなく、「距離」も伸び縮みするということです。「距離」は、「空間」と考えることができるので、「時間」とともに、「空間」も伸び縮みするということが分かります。
宮沢賢治の童話に「銀河鉄道の夜」という作品があります。そのイメージを借りて、宇宙空間を走行する列車があるとします。今、地球発木星行きの銀河鉄道が、宇宙空間を走行しているとします。地球と木星の中間地点に火星が位置するとし、火星に駅があるとします。しかし、この列車は急行なので、火星の駅は通過します。それでは、次の図.20を見てください。銀河鉄道の客車の中間に、投光器を2つ、背中合わせに置きます。投光器を向ける方向は、列車の進行方向とその逆方向です。2つの投光器を同時に点灯させると、光は客車の前の壁と後ろの壁に同時に到達します。
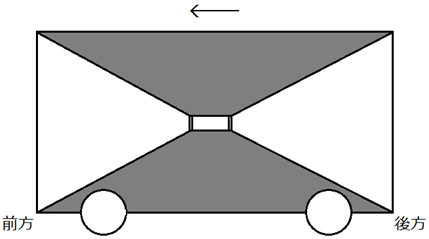
図.20 投光器から放たれた光は、同時に壁に到達する
今、この点灯を、火星の駅を通過する最中に行ったとします。すると、駅のホームに立っている人と客車内の人とでは、光の見え方が変わってきます。駅のホームから見ると、光は客車の後ろに早く到達し、遅れて客車の前の壁に到達するように見えるのです。列車の進行方向に向かう光は、客車の前の壁に到達する間に、客車自体が進んだ距離がプラスされるので、光の進む距離が加算されることになります。つまり、距離が増えても、光の速度は変わらないので、時間が増えることになります。一方で、列車の進行方向と逆に進む光は、後ろの壁まで到達する間に、客車が進んだ距離が引かれるので、光の進む距離は減ることになります。つまり、距離が短くなっても、光の速度は変わらないので、時間も短くなるのです。しかし、火星の駅を通過する最中にこの点灯を行っても、客車内にいる人には、光は客車の前と後ろの壁に同時に到達するように見えます。つまり、観測者の位置によって、時間の進み方が異なるということが起こるのです。これは、観測者の位置が変わっても、光の速度が一定なために起こる現象です。
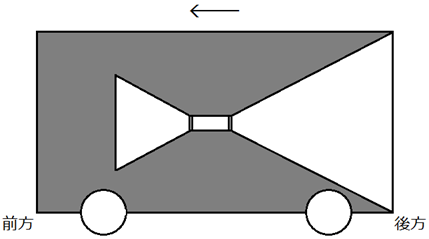
図.21 列車の前方では時間が伸びて、列車の後方では時間が縮むことになる
さらに、銀河鉄道のイメージを借りて、光の速度と時間との関係を、もう少し考えてみましょう。先ほどの銀河鉄道で、客車に投光器を置いたとします。今度は、投光器の向きを、客車の天井に向けたとします。天井には、鏡があって、天井まで届いた光は、再び床に戻るとします。ここで、客車内の人には、この光の動きは、垂直に行き来するように見えます。
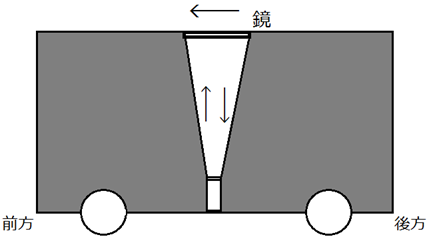
図.22 客車内の人には、光は垂直に行き来するように見える
ところが、これが火星の駅のホームに立っている人には、列車の動きに伴って、光が三角形の斜辺を進むように見えるのです。これは、光の進む距離から考えると、客車内にいるときと駅のホームにいるときでは、光の進む距離が違うと考えられます。
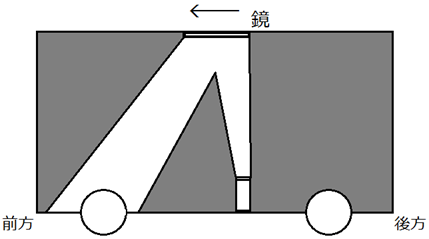
図.23 駅のホームに立っている人には、光の移動距離が増えて見える
光の速度は常に一定なので、距離が大きくなれば、時間の長さも大きくしなければなりません。そして、この考えに基づけば、駅のホームに立っている人から見ると、客車内では、時間が遅くなることになります。これを言い換えると、「静止している場所から動いている物体を見ると、動いている物体では、時間の進み方が遅くなる」ということなのです。仮に同じ運動をするとしても、動いている物体の方が、長い時間をかけてその運動を行っているように見えるため、時間が遅れて見えるという訳です。
それでは、列車の中にいる人にとっては、外部の時間の方が早く進むのかといえば、そうではありません。今度は、外部の時間の方がゆっくり流れるのです。これは、速度が相対的なものだからです。列車の中から外の風景を見ると、景色が流れるように見えますよね?これは、列車の中の人から見れば、自分が静止していて、逆に外の景色が動いているように見える訳です。「どちらが本当に止まっているのか」と考える必要はなく、誰もが「自分は止まっている」と考えて、それぞれが時間の尺度を持てばよいのです。
(6) 時空の歪みと一般相対性理論
アインシュタインが1905年に発表した特殊相対性理論では、それまで別々に扱われていた「時間」と「空間」が、1つの「時空」として統一されました。「時間」と「空間」は、ばらばらに変化するのではなくて、連動して変化することが、特殊相対性理論によって明らかになったのです。私たちの空間は、「縦」・「横」・「高さ」の3つのベクトルで表現できます。これは「3次元空間」と呼ばれるものですが、特殊相対性理論では、「時間」という第4のベクトルが存在します。3次元空間に「時間」というもう1つのベクトルを足して、「4次元空間」と呼んでいます。そして、アインシュタインが1915年に発表した一般相対性理論では、それまで「中身」と「入れ物」として別々に扱われていた「物質」と「時空」が統一され、「時間」・「空間」・「物質」のすべてが1つにまとめ上げられたのです。
ここで、「時空」という言葉が出てきたので、密接な関係にある重力について考えてみましょう。一般相対性理論では、時空は「物質の存在」によって歪み、この「歪み」が重力の正体であると説明されています。例えば、座布団の上に、スイカを載せたとします。座布団は、スイカの重みで沈み込んでしまうのが想像できると思います。その周りにビー玉を転がすと、ビー玉は座布団の沈み込みに沿って、そのままスイカの周囲を回り続けます。歪みのないところでビー玉を転がすと、まっすぐ転がってくので、周囲を回り続けるということは、スイカによる歪みに引き寄せられているということです。それを、「重力があると時空が歪む」、逆に言えば、「時空が歪んでいることが重力の存在を示している」と考えるのです。ニュートンの万有引力の法則は、物と物とが引き合う力を「引力」と呼んでいましたが、アインシュタインは、物と物とが引き合っているのではないと気が付いたのです。隕石が地球に落ちるのも、隕石と地球とが引っ張り合うからではなく、地球によって歪められた時空により、隕石が軌道を変えたためと説明されるのです。

図.24 隕石が地球に落下するのは、地球によって「時空」が歪められているからである
一般相対性理論は、水星の「近日点」のズレを説明したことでも、正しさが実証されています。水星は、太陽の周りを楕円の軌道を描いて回っていますが、太陽に一番接近する地点を「近日点」と呼びます。ここで、万有引力の法則で計算した近日点と、実際に観測した近日点との間に、微妙なズレがあったのですが、一般相対性理論による計算では、実際の観測結果と一致したのです。こうして物理学の主役は、万有引力の法則などの「ニュートン力学」から、アインシュタインの「相対性理論」へと継承された訳です。ここで注意してほしいのは、万有引力の法則が間違っている訳ではないということです。重力が小さい物体の動きでは、万有引力の法則でほぼ正しく計算ができるのです。これに対して一般相対性理論は、質量が非常に大きい物体などの場合にも対応しているのです。
物体の質量によって歪むのは、「空間」だけではありません。重力により、「空間」だけでなく、「時間」も歪められてしまいます。つまり、重力が大きければ大きいほど、その場所の時間は、遅れることになるのです。現在、最も精度が高い時計は、原子時計とされています。原子時計は、原子から出る放射線の振動数を測定して時を刻むのですが、これは電子が正確な周期運動をしているからです。高精度のもので3,000万年に1秒、低精度のものでも3,000年に1秒しか狂いがないといわれているほどです。電子の運動は、それだけ規則正しいものなのです。ところが重力が変わってしまうと、規則的な電子の運動に変化が現れます。重力の大きい場所になると、電子の運動が遅くなり、放射線の振動数も遅くなるのです。つまり、時間が遅れるということです。地球上にも重力があるので、無重力の宇宙空間と比較すると、時間が遅れていることになります。しかし、地球程度の重力では、さほど時間に対する影響はなく、1秒当たり100億分の7秒というわずかな値です。太陽では、1秒につき100万分の1秒遅れるといわれています。
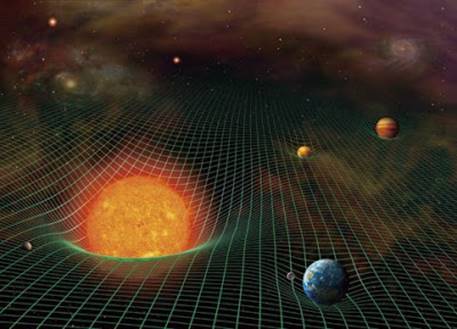
図.25 太陽の表面では、時空が100万分の1ほど歪んでいる
なお、現代人の生活に身近な「GPS(Global Positioning System)」でも、一般相対性理論は実証されています。GPSは、元々アメリカ国防総省が、航空機やミサイルの誘導のために開発したものです。しかし、現在では、自身の位置を知るシステムとして、飛行機や船、自動車などに利用されています。複数のGPS衛星からの電波を受信して、その電波が発信源からどれくらい遅れて到着したかということを計算して、自分の位置を測るのです。しかしながら、GPS衛星は、重力源である地球から離れた衛星軌道上を周回し、地上に比して重力が小さい環境にあって、その分地上よりも時間の経過は早いです。このため、GPS衛星側の内蔵時計は、毎秒100億分の4.45秒だけ遅く進むように調整されています。わずかな調整のように思うかもしれませんが、GPS衛星から送られてくる電波は光速(3.0×108 m/s)なので、調整しない場合に生じる誤差は、距離に換算すると1秒当たりで3.0×108×4.45×10−10=0.1335 mにもなります。つまり、一般相対性理論を考慮しない場合は、GPSは1秒当たりで約10 cmもずれることになります。これほど誤差があったらカーナビは使い物にならないので、今や特殊相対性理論は、生活に必須の理論であるといえるでしょう。

図.26 衛星軌道上では、地上よりも重力が小さいので、時間が早く進む
(7) ブラックホールに落ちると人はどうなるのか?
(i) あらゆる物体がブラックホールとなるシュバルツシルト半径
宇宙には、とてつもなく重力が大きい場所が存在します。それは、「ブラックホール」です。ブラックホールとは、大質量、高密度、高重力の性質を持つ天体のことで、周囲では空間が非常に大きく歪み、あらゆるものを中心方向に引きずり込んでいまいます。太陽の何十倍も重い星が、最終的に燃え尽きて、自分の重力に耐えきれなくなったときに、「超新星爆発」を起こして、ブラックホールになるといわれています。大爆発によって、星の中心部が極限まで圧縮された結果、ブラックホールが生まれるのです。何らかの方法により、地球を半径0.9 cmくらいにまで圧縮する、あるいは太陽を半径3 kmくらいにまで圧縮すると、ブラックホールができあがります。重力は、重力源からの距離が短いほど強くなるので、地球や太陽を小さく圧縮していけば、その表面付近の重力がどんどん強くなり、ついにはブラックホールが誕生するのです。

図.27 「ブラックホール」の周囲の空間はねじ曲げられ、周囲の景色が円形に歪んで見える
このようにある物体を圧縮していったとき、その物体がブラックホールになるような半径を、「シュバルツシルト半径」といいます。これは、一般相対性理論におけるアインシュタイン方程式の「特殊解」として、ブラックホールを理論的に発見したドイツの天体物理学者であるカール・シュバルツシルトの名前にちなんでいます。シュバルツシルト半径を持つ質量に下限はなく、理論上はいかなる微小な質量の物体でも、圧縮すればブラックホールになることが分かっています。シュバルツシルト半径 ![]() は、天体の質量をM、高速度をc、万有引力定数をGとすると、次のように求めることができます。この式に、地球の質量5.972×1024 kgや太陽の質量1.9891×1030 kgを代入することで、地球や太陽がブラックホールになる半径を求めることができます。計算すると、地球では0.9 cm、太陽では3 kmというシュバルツシルト半径を求めることができます。もちろん、地球や太陽をシュバルツシルト半径まで圧縮することは、現代の科学技術力では極めて難しいです。
は、天体の質量をM、高速度をc、万有引力定数をGとすると、次のように求めることができます。この式に、地球の質量5.972×1024 kgや太陽の質量1.9891×1030 kgを代入することで、地球や太陽がブラックホールになる半径を求めることができます。計算すると、地球では0.9 cm、太陽では3 kmというシュバルツシルト半径を求めることができます。もちろん、地球や太陽をシュバルツシルト半径まで圧縮することは、現代の科学技術力では極めて難しいです。
![]()
(ii) 一度入ったら出られない事象の地平面
ブラックホールには、「事象の地平面」と呼ばれる目に見えない表面があります。ただし、固体地球の表面や太陽の表面とは異なって、事象の地平面のところにはっきりとした境界がある訳ではなく、またそこで、空間の性質が急激に変わる訳でもありません。何らかの理由で、事象の地平面を超えてブラックホールの内部に入り込んだとしても、境界を越えたことが分かりません。もし、宇宙船でそこに入っていくとすると、事象の地平面を通り過ぎるときは、何も感じません。突然重力が強くなるようなこともないのです。ただし、事象の地平面は、そこから一歩でも中に入ってしまったら、もう二度と外へ出ることのできない境界面です。そこから抜け出すには、光速を超える必要があります。つまり、ブラックホールの内部からは、光さえも抜け出せないのです。そのため、ブラックホールの内部の出来事は、外側から観測することができません。しかし、ブラックホールの近くに別の星が近付くと、ブラックホールは強い重力で、その星の表面のガスを吸い込みます。このとき、ガス同士が衝突して、数百万度の高温になり、強い「X線」を放ちます。このX線を観測することで、ブラックホールの存在を間接的に確認することができるのです。

図.28 ブラックホールが別の星の表面のガスを吸い込むときに、強い「X線」が放出される
また、事象の地平面の中心には、「重力の特異点」と呼ばれる空間が存在します。特異点は、「重力と密度が無限大になる」という、完全に地球上での物理法則を無視した特性を持っています。時間は、重力の影響を受けると進み方が遅くなりますが、ブラックホールのようなとてつもない大きさの重力に遭遇すると、ついには止まってしまうのです。例えば、ブラックホールに向かって、宇宙飛行士を乗せた宇宙船が飛んでいるとします。宇宙船を離れた場所から観測すると、宇宙船はブラックホールに近付くにつれて、だんだんスピードが遅くなっていきます。そして、ある地点で、ピタリと止まったまま、動かなくなってしまいます。通信しようとして、こちらから電波を発しても、返事は返ってきません。宇宙船からの電波は、ブラックホールの重力によって、観測者まで届かないのです。それでは、宇宙船の中はどうなっているのかというと、船内の宇宙飛行士は、観測者が感じた時間の遅れに全く気が付きません。動作が緩慢になるようなこともなく、通常通りに時間は進行しているのです。つまり、観測者と宇宙飛行士とでは、時間の進み具合が違うのです。観測者から見て、宇宙船の動きが停止したように見える地点が、「事象の地平面」です。この事象の地平面が、ブラックホールから抜け出せるか、抜け出せないかの境目になります。残念ながら、事象の地平面を超えてしまった宇宙飛行士は、もう二度と戻ってくることはできません。
事象の地平面を超えた直後は、まだ重力があまり強くないので、宇宙船も、そのままの形を保っています。しかし、だんだんとブラックホールの中心に近付くにつれ、重力は急激に強くなっていきます。宇宙飛行士が足から近付いた場合には、足にかかる重力が、頭にかかる重力よりはるかに大きくなります。そのため、体は細長くなるように縦に引き伸ばされ、最後には、粒子レベルまで引き裂かれてバラバラにされてしまいます。物理学者は、このような潮汐力の効果により起こる現象を、「スパゲティ化現象」と呼んでいます。ブラックホールは、光さえも抜け出せないので、宇宙飛行士が、宇宙船と共にバラバラに引き裂かれる光景は、ブラックホールから離れている観測者には届きません。宇宙飛行士自身は、すぐにバラバラに引き裂かれるのですが、外にいる観測者には、宇宙船が事象の地平面で、永遠に停止しているように見えてしまうのです。まさに、「時間が止まった」かのような感じに見えるのかもしれません。現代の物理学では、ブラックホールの中心では、時間や空間の概念が消えてなくなると考えられています。ブラックホールに落ちてしまった宇宙飛行士の時間も、終焉を迎えることになるでしょう。

図.29 ブラックホールに落ちた人は、「スパゲティ化現象」によって細長く引き裂かれてしまう
なお、人類はブラックホールまでたどり着いたことはありませんので、以上のことはあくまでも理論上の話です。しかし、計算によれば、天の川銀河の中だけでも、1億〜10億個ものブラックホールがあると考えられています。物理学者の中には、「ブラックホールは別世界へのトンネルである」と考える人もいるようです。一般相対性理論からは、あらゆる物質を放出するという「ホワイトホール」の存在が導かれ、ブラックホールとホワイトホールが、一方通行のトンネルを通じて繋がっているため、ブラックホールに吸い込まれた物質が、ホワイトホールから放出されるというのです。ホワイトホールは、数学的には成立するものの、実際の天体として存在しうるかどうかは、今のところは全く分かっていません。
(iii) ブラックホールの蒸発
ちなみに、ブラックホールは、長い時間をかけて徐々に蒸発しており、やがて消滅してしまうという説があります。イギリスの物理学者であるスティーブン・ホーキングによると、ブラックホールの事象の地平面からは、物質を構成する最小単位である「素粒子」が放出されているというのです。たとえ真空でも、「無」という状態はありません。ミクロの素粒子が突然発生したり、突然消滅したりしているのです。例えば、プラスの素粒子とマイナスの素粒子が衝突すると、突然両方とも消滅してしまいます。また、突然何もないところから、プラスの素粒子とマイナスの素粒子が発生したりもします。通常、これらの素粒子は、発生してもすぐに衝突して消滅してしまうのですが、事象の地平面付近でこれらの素粒子が発生した場合、衝突して消滅する前に、マイナスの素粒子がブラックホールに吸い込まれ、もう一方のプラスの素粒子が反動で飛び出してきます。この飛び出す素粒子が、あたかもブラックホールから放出されているように見えるのです。
ブラックホールは、マイナスの素粒子を吸い込むと、質量が減少していきます。これは、マイナスの素粒子には、負のエネルギーがあるからです。質量が減少すれば、半径も縮んでいきます。そして、半径が小さくなればなるほど、ますます素粒子の放出が激しくなります。ブラックホールは、非常に温度が低いのですが、半径が小さくなるにしたがって、少しずつ温度が上がってきます。温度が上がって、周りの空間より温度が高い状態になると、熱が放出されるようになるのです。このような現象を、「ブラックホールの蒸発」と呼んでいます。強力な重力ですべてを飲み込むブラックホールでも、何かしらのエネルギーが放出されて、大きさが少しずつ縮小しているのです。なお、ブラックホールが完全に蒸発してしまうには、宇宙の年齢である138億年よりも、さらに長い年月が必要だといわれているので、観測するのは難しいでしょう。
(8) 流れた時間は元には戻せない
(i) 不可逆的な時間の矢
「時間の矢」という言葉があります。時間には、「過去」と「未来」の非対称性がある――つまり、時間は、「未来」に向かって流れるけど、「過去」には戻らない――ということを表現した言葉で、矢が一直線に進むように、時間も「未来」という一方向のみに流れるという意味です。それでは、なぜ時間は、「未来」にしか流れないのでしょうか?時間が「過去」に流れるということは、ありえないのでしょうか?ごく当たり前のことですが、難しい問題でもあります。
自然界には、「可逆」と「不可逆」という2種類の変化の仕方があります。可逆とは、変化を逆戻りさせると、再び元の状態に戻れることです。それに対して、不可逆とは、変化を逆戻りさせて、元の状態に戻すことができないことです。可逆の例としては、水が凍ることや、氷が溶けることが挙げられます。水は温度が0℃で凍りますが、温度が上がれば、再び氷から水に戻ります。その逆も然りです。不可逆の例ですが、水の入ったコップがテーブルから落ちて、粉々に割れてしまったとします。こうなると、元の水の入ったコップには戻すことができません。ビデオに撮影して逆回しで再生すれば、元に戻ったように見えますが、現実のガラスの破片が自然にくっついて、元のコップに戻るようなことはありえません。何とも当たり前なことですが、これが自然界の法則とされているのです。

図.30 割れたコップを完全に元の状態に戻すことはできない
さて、物理学では、「時間の流れ」も、不可逆的な変化と考えられています。「コップ」から「割れたガラス片」と変化するように、「整然とした状態」から「乱雑な状態」へと変化していくのが、自然界の掟です。「乱雑な状態」から「整然とした状態」に変えるには、そこに何らかのエネルギーが必要になってきます。例えば、ガラスの破片を集めて、熱で溶かし、再び同じコップを作るなどが考えられますが、完全に同じものを再現できる訳ではありません。時間が1つの方向にしか流れないのは、それを逆に戻すためのエネルギーが存在しないから――という考えもありそうです。逆に考えれば、過去に戻るためには、莫大なエネルギーが必要ともいえそうです。現在の人間の力では、そのような莫大なエネルギーは、手に入れることができない訳です。
(ii) エントロピーと死の関係
熱力学に、「エントロピー」という言葉があります。エントロピーというのは、「エネルギーの質」のことで、「乱雑さの度合い」と表現されることも多いです。エントロピーが高いほど、質の悪いエネルギーであり、質の悪い高エントロピーのエネルギーを、手を加えずに質のよい低エントロピーのエネルギーにすることはできない――これを「熱力学第二法則」といいます。熱のようなエネルギーは、質が悪くてエントロピーが高いです。例えば、中央を仕切られた水槽があるとします。仕切りの一方には熱湯を入れ、別の一方には水を入れておきます。仕切りを取ると、時間の経過とともに、熱湯と水とは混じり合い、ぬるいお湯になります。この現象は、熱湯の「熱が拡散した」ともいえる訳で、エントロピーが増大したと表現される訳です。自然界では、熱は、温度の高い部分から低い部分に流れていきます。そして、高低差のある熱源の温度のちょうど中間ぐらいの温度で、熱の移動がストップします。これは「熱平衡状態」と呼ばれ、エントロピーが最大の状態です。時間とともに熱は拡散、つまり冷めていき、エントロピーが増大していくのです。
熱は、目で見えるものではありません(ただし、サーモグラフィーのように、物体から放射される赤外線を分析し、可視化したものはあります)。そのため、具体的なビジュアルとして、イメージし辛い面もあります。ここで、ミクロの世界に視点を移すと、「熱は原子や分子の運動エネルギー」と表現できるのです。金属のような固体は、原子同士が固く結びついていて、運動しているようなイメージはありませんが、実は小刻みに振動しているのです。そこへ熱が加えられると、原子の運動が活発になって結合が弱まり、液体へと変化します。さらに熱を加えると、気体へと変化していきます。原子の運動が活発になり、拡散して乱雑になり、エントロピーが増大するのです。原子のレベルで考えると、「エントロピー」というものが、理解できると思います。
ここで、宇宙に目を向けてみます。宇宙は、今から約138億年前、エントロピーの小さい状態で誕生し、それが大きく膨張することによって、現在の宇宙になっています。これを「ビッグバン理論」といいます。ビッグバンを起こした直後の宇宙は、すべての物質とエネルギーが一カ所に集まった、高温度・高密度の状態にありました。ビッグバン直後の温度は「1プランク温度」と呼ばれ、その値は、およそ1.4×1032℃と推定されています。1プランク温度以上の温度で、物理的に意味のあるものは知られていません。その温度が、時間の経過とともに冷めているのです。私たちの宇宙は、こうしている間にもどんどん膨張していますが、それは時間が経過するとともに、エントロピーが増大(温度が低下)しているということなのです。宇宙のエントロピーがどんどん増大していくと、やがて宇宙は均一な温度で、均一な物質が静止して広がっているというような状態になります。このような状態を、物理学者は「宇宙の熱死」と呼んでいます。

図.31 現在の宇宙の温度は−270℃であり、宇宙が膨張を続けることにより、温度はさらに低くなっていく
人間は、食物を摂取しなければ生きていけません。食物を摂取すれば、必ず排泄します。この「食物を摂取する」という行為は、実は「自身のエントロピーを下げる行為」といわれているのです。人間は、自然環境から「食物」という秩序あるものを摂取して、「排泄物」という無秩序なものに変化させています。生物は、秩序ある存在であり、摂取と排泄を繰り返すことで、自らの秩序を保っているのです。
このことを、エントロピーという視点で考えてみます。生きることは、「自らの秩序を保つために、エントロピーを下げていくこと」と考えます。死んでしまうと秩序が保てなくなり、エントロピーが増大することになります。人間は、自分のエントロピーが増大しないように、自然界から「食物」という質のよい低エントロピーのエネルギーを摂取して、外部に「排泄物」という質の悪い高エントロピーのエネルギーを捨てています。食物を摂らないと、エントロピーが増大する――つまり、死を迎えることになります。こうしてみると、「エントロピーが増大する」という方向と、「時間が未来に向かっていく」という方向は、同じ方向なのかもしれません。
ただし、時間とエントロピーが同じ方向に進むといっても、この2つは、全く同一のものではないようです。例えば、閉ざされた箱の中に、熱湯を入れた瓶を入れておくと、瓶の熱は箱の中の空気に伝わり、ある程度時間が経過すると、箱の中の空気と瓶のお湯は熱平衡状態になり、同じ温度で安定化します。熱平衡状態になると、熱の移動はなくなり、エントロピーの増大も止まります。しかし、エントロピーの増大が止まっても、時間はそのまま流れ続けるのです。人生には、いずれ終わりがやってきますが、時間だけは、その後も流れ続けます。延々と流れ続ける時間と比較すれば、人間の存在なんて、ちっぽけなもののような気がしてきます。

図.32 熱湯を部屋で放置すると、熱湯の熱は空気を伝って部屋に拡散する
(iii) マクスウェルの悪魔は存在するのか
ところで、「マクスウェルの悪魔」というものがあります。これは、19世紀に活躍したイギイスの物理学者であるジェームズ・クラーク・マクスウェルが発案した思考実験です。例えば、真ん中に仕切りがある箱があるとします。箱の右と左の部屋には、それぞれ同じ温度の気体が閉じ込められています。つまり、熱平衡の状態にある訳です。「悪魔」が真ん中の仕切りのところにいて、箱の右側から「速度の速い空気分子」が走ってくると、悪魔は扉を開けます。一方、箱の左側から「速度の遅い空気分子」が走ってくると、悪魔は扉を閉めます。これをずっと続けていると、左の部屋には速い分子ばかりが、右の部屋には遅い分子ばかりがたまります。速度が速いということは、温度が高いということなので、左の部屋は温度がどんどん高くなり、右の部屋は温度がどんどん低くなるという現象が発生します。これを再現することは可能なのでしょうか?
当たり前のことですが、通常このようなことは考えられません。「そんな悪魔など存在しない」と言えばそれまでなのですが、実は、この悪魔の存在を科学的に否定するのに、何と100年以上の年月がかかってしまったのです。何という時間の無駄だろうと思うでしょうが、マクスウェルの悪魔について考察を繰り返した結果が、物理学や情報科学などの発展に寄与し、現在に活かされているのです。100年以上もの間、科学者が悩んだのも、無駄ではなかったようです。
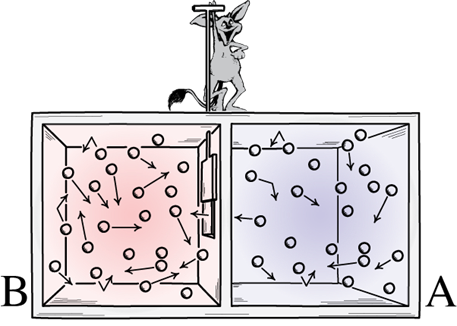
図.33 「マクスウェルの悪魔」が存在すれば、空気からエネルギーを取り出すこともできる
さて、再び真ん中に仕切りがある箱を用意します。今度は、左側に気体の分子を入れておき、右側を真空にしておきます。仕切りを取ると、箱の左側にも右側にも均一に気体分子が拡散していきます。これをそのまま放置しておけば、このまま安定した状態が続くというのは理解できるでしょう。しかし、長時間このままにしておくと、いつかは箱に拡散した気体分子が勝手に動いて、再び元の左側の部屋に集まり、右側の部屋が真空になるというようなこともあるというのです。これは、「有限の時間であれば、必ずいつかは原点の状態に回帰する」という定理です。
そんな馬鹿なことが起こるはずはないと思うかもしれません。しかし、宇宙の年齢である138億年よりもはるかに長い年月が経過すれば、このように完全な元の状態に戻ることもあり得るという考え方で、「ポアンカレの回帰定理」と呼ばれる学説が存在するのです。このように、あるプロセスの時間スケールが、宇宙膨張の時間スケールよりも長くなってしまうことを、「宇宙膨張から落ちこぼれる」と表現します。この落ちこぼれにより、始めは高エントロピーの状態にあっても、時間の経過とともに、いつかは低エントロピーの状態になっていきます。まさに、マクスウェルの悪魔のような存在がいるかのようです。これが本当に起こるのかどうか、とても人間には観測できそうにないのが残念です。
(9) タイムマシーンは存在するのか
(i) 特殊相対性理論で未来に行く
「タイムマシーン」で過去に戻るのはさておき、未来に行くことは、理論上可能です。アインシュタインの特殊相対性理論を思い出してください。運動する物体の速度が十分に大きければ、時間の遅れを実感できるようになります。つまり、光の速度に近い宇宙船に乗って宇宙を旅行すれば、地球に帰還したときには、地球上では未来になっているのです。「地球にいる人の経過時間」と「運動する物体の経過時間」の関係を計算してみましょう。光速を ![]() とすると、次の式から計算することができます。
とすると、次の式から計算することができます。

例えば、光速の99.999%の速さで飛べる宇宙船があったとします。その宇宙船に乗って、1年間宇宙を旅行して、地球に帰還したとしましょう。「運動する物体の経過時間」は1年間、「物体の速度」は ![]() なので、「地球にいる人の経過時間」は、次のように求めることができます。
なので、「地球にいる人の経過時間」は、次のように求めることができます。
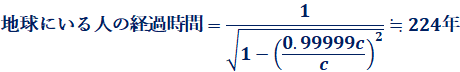
つまり、この宇宙船に1年間乗って地球に帰還すると、地球では224年もの歳月が流れていることになるのです。日本のSF作品などでは、童話「浦島太郎」の主人公である浦島太郎に起こった「竜宮城で3日過ごして戻ってくると300年経っていた」という出来事になぞらえて、この現象を「ウラシマ効果」と呼んでいます。藤子不二雄の作品である「ドラえもん」では、「浦島太郎自身が、実は海でなく宇宙に連れていかれて、ウラシマ効果を体験したのではないか」と考えたドラえもんたちが、タイムマシーンでその真偽を確かめに行くというエピソードが登場します。

図.34 浦島太郎が竜宮城で過ごした日々は数日だったが、地上では随分長い年月が経っていた(画像は香川県の詫間大橋の浦島太郎像)
ちなみに、光と同じ速さなら、もっと未来に行けるのではと思われますが、それはできません。前述の光速の99.999%はおろか、光速の1%の速度を出すことも、現実には不可能に近いのです。これは、特殊相対性理論では、光速に近付けば近付くほど、質量が増加してしまい、加速するためにさらなるエネルギーが必要となるからです。質量がある私たち人間は、光速と同じ速度になることは、現実的に不可能であると考えられています。
(ii) 宇宙船のテクノロジーを考える
それでは、光速に近付ける宇宙船として、どのようなテクノロジーが考えられるでしょうか。まず、「核融合」を利用した宇宙船が考えられます。太陽と同じように水素を燃料にして「核融合反応」を起こし、推進するシステムです。核融合反応では、「軽い元素」が衝突して「重い元素」へと変わっていく過程で、エネルギーを放出していきます。しかし、これでも光速の10%程度が限界といわれ、大量の燃料を必要とするため、宇宙船は巨大化せざるを得ません。そこで、「恒星間ラムジェット」というものが発案されました。これは、核融合を利用するのですが、宇宙空間に散在している水素分子を主とする「星間物質」を、強力な磁場によってかき集めて燃料とするので、宇宙船の小型化が可能です。しかし、速度はやはり光速の10%程度が限界だといわれ、強力な磁場が宇宙船内の機器や人体に与える影響も不明です。

図.35 「恒星間ラムジェット」のイメージ図
もっと莫大なエネルギーを得る方法として、「反物質」を利用するという考えもあります。反物質とは、通常自然界に存在する陽子や電子などの粒子と、反対の電荷を持つ粒子のことです。例えば、「電子」はマイナスの電荷を持ちますが、「反電子」はプラスの電荷を持ちます。反物質と普通の物質(正物質)を衝突させると、反物質と正物質が完全に消滅します。そして、それらの失われた質量が、莫大なエネルギーに変換されて放出されるのです。高エネルギーの粒子同士を加速器で衝突させると、安定した反物質が生成することは確認されており、これを安全に保存できるなら、将来的なエネルギー源として利用できる可能性があります。理論上では、たった1 gの反物質から、スペースシャトルの外部燃料タンク23個分ものエネルギーを取り出すことができます。しかし、いずれの宇宙船も、実現に至るまでの課題は多く、まだまだ遠い未来の技術のようです。

図.36 現在の宇宙船の多くは、化学燃料を推進剤として利用している
(iii) 過去に戻るにはどうすればよいか
光速に限りなく近付くことで、未来に行くことは可能だということは分かりました。それでは、過去に戻る方法は、何かないのでしょうか?1つの考え方として、「時空を歪ませて、時間の向きを過去に向かわせる」という方法があります。そのためには、時空を歪ませるほどの大質量の物体が、超高速で自転する必要があるのです。そして実は、高密度でかつ高速で回転する物体が、宇宙には存在します。先にも述べた「パルサー」と呼ばれる中性子星です。パルサーは、半径10 kmほどの大きさに、太陽ぐらいの質量がある星です。高速で自転しているので、その周りの時空は歪んでいると予想されています。宇宙船に乗って、パルサーの周りを一周すると、出発したときと同じ時間に到着するという、不思議なことが起こるかもしれません。未来に流れるはずの時間が、過去に流れるという現象です。しかし、地球に最も近いパルサーでも、およそ200光年と結構な距離があるため、パルサーまでたどり着くこと自体、現在の科学技術力では不可能に近いです。

図.37 「パルサー」の周りを一周すれば、過去に戻れるかもしれない
また、時空の歪みを、人工的に作り出せないかと考えた人がいました。アメリカの物理学者であるフランク・ティプラーです。無限に長くて、超高密度の筒状の物体があるとします。とても細長いヒモのような円柱をイメージして下さい。そして、これを超高速で自転させます。すると、円柱の周りの時空が歪み、「時間の矢が未来へと進まない状態」になります。つまり、時間の矢が輪になるというのです。この「ティプラー・マシン」を利用すれば、タイムトラベルを現実にすることができるのでしょうか?まず、長さが無限ということは、とても人間の力では実現不可能な訳で、これを有限の長さとします。しかし、それでも直径10 km、長さ100 kmの円柱にすると、質量は太陽と同程度のレベルが要求されるようです。また、長さを有限とすると、円柱は自身の重力で上下から押し縮められ、潰れてしまうそうです。場合によっては、ブラックホールができあがることも考えられます。あまりにもスケールが大きすぎて、人間には手に負えない技術のようです。

図.38 「ティプラー・マシン」のイメージ図
また、2017年に「重力波」の観測における功績で、「ノーベル物理学賞」を受賞したアメリカの物理学者であるキップ・ソーンは、「ワームホール」を使えば、時空間のワープやタイムラベルが可能であると述べています。ワームホールとは、3次元空間上の離れたA地点とB地点を、別次元の空間を利用して結ぶ「秘密のトンネル」のような穴です。ワームホールは、「同じ時間」で2つの場所を瞬時に結ぶことができます。実際に存在が確認された訳ではなく、飽くまで理論上のものです。
まず、通過可能なワームホールを用意して、AとBの両地点の出入り口から、お互いの世界を覗くことができるとします。Aの出入り口から入っていくと、瞬時にBの出入り口から出ることができると考える訳です。今、Aの出入り口が宇宙船の船内にあり、Bの出入り口が地球にあったとします。宇宙船は光速に限りなく近付いて、宇宙を旅したとします。そして1年後、宇宙船は帰還しました。地球では、ウラシマ効果により、1年が経過している宇宙船内よりも早く時計が進み、4年が経過していたとします。ここで、どういうことが起こるでしょうか?宇宙船にあるAの出入り口は1年しか経過していないので、ここから地球にあるBの出入り口を覗くと、そこから見える地球も1年しか経過していません。つまり、地球に残って4年が経過した人が、地球に到着した宇宙船にあるAの出入り口からBの出入り口に出ると、3年前の地球に行けます。こうして、過去と未来とを結ぶトンネルが、ワームホールを介して地球上に完成したことになります。

図.39 「ワームホール」という名前は、「リンゴの虫食い穴」に由来する
それでは、ワームホールは、どうやって作ればよいでしょうか。考え方としては、2つの方法があります。1つ目は、「ワームホールはミクロの世界に存在しており、ミクロの世界のワームホールを、人間が通れるぐらいに拡大する」というものです。ミクロの世界では、絶えず素粒子が発生したり、消滅したりしていると考えられており、ミクロの世界は、多くの空間が押し込められた「多次元空間」であると考えられています。ミクロの世界に存在するワームホールの大きさは、10−35 mほどだといわれています。原子の大きさが10−10 mですから、非常に小さいことが分かります。しかし、どうやってミクロのワームホールを人間が通れる大きさに拡大するのかは、現在では全く分かっていません。
2つ目は、「最初から人間が通れるぐらいのワームホールを作る」というものです。しかし、現在の人類の科学技術力では、ゼロからワームホールを作ることは不可能です。人間が通れるようなワームホールを作るためには、普通の物質ではなく、エネルギーがマイナスであるような不思議な物質が必要です。このような物質を、「エキゾチック物質」といいます。エキゾチック物質は、もちろん自然界には見つかっていません。人類がタイムマシーン用のワームホールを調達できるようになるのは、何百年も先になってしまいそうです。
(10) 時間に関するパラドックス
(i) 双子のパラドックスをどう説明するか
時間にまつわる不思議な現象として、「双子のパラドックス」というものがあります。これは、アインシュタインが提唱した特殊相対性理論において、「時間の遅れに関する理論に矛盾があるのではないか」という問題提起です。例えば、双子の兄弟のトムとロバートがいるとします。兄のトムが宇宙飛行士で、光速に限りなく近い速度が出せる宇宙船に乗って、宇宙旅行をしばらくしてから、地球に帰還したとします。この場合、宇宙旅行をしたトムは、特殊相対性理論により、時間の進み具合が遅くなります。地球に残った弟の方が、兄のトムよりも歳を取っていることになります。これが、特殊相対性理論が導く結果で、先にも説明した「ウラシマ効果」です。
双子のパラドックスは、実際には、このようなことが起こらないのではないかという指摘です。例えば、アインシュタインは、特殊相対性理論において、「すべての運動は相対的」と述べています。それなら、双子の兄弟の運動も互いに相対的であり、宇宙船にいる兄のトムを基準にすると、地球にいる弟のロバートの方が、宇宙船から光速に限りなく近い速度で遠ざかっていることになります。つまり、光速に近い速度で運動しているのは、地球にいる弟のロバートであるという見方もできる訳です。そうすると、弟のロバートの方が時間の進み方が遅くなり、兄のトムの方が歳を取った状態になることも考えられます。これでは先の結果と逆になり、特殊相対性理論が成立せず、ウラシマ効果も起こらないことになります。これは、一体どういうことなのでしょうか?
このパラドックスは、双子の兄弟の運動が、対称ではないことから解決されます。それ故に、特殊相対性理論は矛盾なく成立し、ウラシマ効果は起こるのです。兄のトムが乗っている宇宙船は、地球を飛び立つときやUターンして戻ってくるときに、加速や減速をする必要があるので、少なくとも一時的に「加速系」にいることになります。それに対し、弟のロバートは、地球に残っているので、加速や減速のない「慣性系」にいます。すなわち、兄のトムが置かれた状態と、弟のロバートが置かれた状態では、与えられた条件がそれぞれ異なっており、両者の運動は、同等の関係とはいえないのです。両者を比べると、光速に限りなく近い速度で運動しているのは、宇宙船に乗っている兄のトムになる訳で、兄のトムの時間の流れが一方的に遅くなります。双子のパラドックスは、やはり間違った理論なのです。
ちなみに、宇宙船に乗った兄のトムから、地球に残った弟のロバートを見ると、どのように時間が進んでいるように見えるのでしょうか?簡単に説明してみます。宇宙旅行の「往路」に関しては、互いの運動は「相対的」なので、弟のロバートの方が、ゆっくりと歳を取っているように見えます。問題は、兄のトムがUターンをしたときに、何が起こるのかということです。このとき、兄のトムの速度が変わったことに応じて、「同時刻線」が傾きを変えます。つまり、宇宙旅行の「復路」に関しては、弟のロバートの方が、速く歳を取るように見えるのです。この結果、「兄のトムが地球に帰還したときには、弟のロバートの方が歳を取っていた」というようになります。

図.40 双子の宇宙飛行士マーク・ケリー(左)とスコット・ケリー(右)がいる。実際に双子のパラドックスが起こることはない
(ii) タイムパラドックスが起こるとどうなるか
「タイムパラドックス」とは、仮にタイムトラベルが可能になった場合に起こると予想される、矛盾や変化のことです。タイムパラドックスは、時間に逆行するタイムトラベルが不可能だとする証拠として使われてきました。つまり、タイムパラドックスがあるから、タイムトラベルは不可能であるという理論です。
有名なタイムパラドックスの例として、科学の法則には、「質量保存の法則」というものがあります。どのような化学変化が起こっても、物質の総質量は変化しないという大原則で、「近代化学の父」とも称されるフランスの化学者であるアントワーヌ・ラボアジエが発見した法則です。ここで、ケンイチという人物が、タイムトラベルで過去に行き、過去の自分と対面したとします。これでは、自分と同じ質量のケンイチが、この世に突然発生したことになり、実量保存の法則が成立しないことになります。
その他にも、このようなことが考えられます。例えば、過去にタイムトラベルをしたケンイチは、自分の父方の祖父を拳銃で殺してしまった。この場合、ケンイチの父親が生まれてこないことになり、結果としてケンイチも生まれてこないことになる。したがって、ケンイチは消滅して祖父を殺すこともできなくなるから、その後、またケンイチが生まれることになる。すると、やはりケンイチは、タイムトラベルをして祖父を殺す――このような堂々巡りになってしまいます。ロバート・ゼメキス監督の映画「バック・トゥ・ザ・フューチャー」でも、主人公のマーティが過去へとタイムトラベルをしたことで、母ロレインと父ジョージの出会いが妨げられ、二人が恋人同士にならず、マーティの存在が消えかかってしまう、というシーンが登場します。

図.41 映画「バック・トゥ・ザ・フューチャー」では、タイムパラドックスによって、主人公のマーティの存在が消えかかった
物事には、必ず「原因」があって、「過程」があって、「結果」へとつながっていきます。それを「因果関係」といい、それは決して崩れることがあってはならないものです。因果関係の不一致を引き起こすようなタイムパラドックスを回避するには、どのような理論が必要なのでしょうか。例えば、「過去は決して改変できない」という考え方があります。ケンイチが祖父を殺そうとしても、その試みは、自然の法則あるいは何らかの要因により妨げられ、相手は必ず生き延びるというものです。祖父を拳銃で撃とうとしても、銃弾が外れたり、そのような行為の成功を妨げる何らかの事象が発生したりするというのです。結果として、ケンイチは歴史を改変することができず、タイムトラベル自体がなかったことになるというのです。
それと密接に関連する解釈として、「時間線には自己修復能力がある」という考え方もあります。些細な改変は一時的なゆらぎに過ぎず、その後は収束して、未来の方向性に大きな影響を与えないというものです。例えば、タイムトラベルをした人が、恋人が交通事故で死ぬのを防いだとしても、別の何らかの原因(階段を踏み外す、食事を喉に詰まらせる、流れ弾に当たるなど)によって、その恋人は結局死ぬことになるというものです。イギリスで放映されている世界最長の人気SFテレビドラマ「ドクター・フー」では、「時間は水の流れのようなもの」と説明しています――その流れにダムを作ったり、方向を変えたり、一時的にせき止めたりすることは可能だが、低い方へと流れる全体的方向を変えることはできない――ということです。

図.42 テレビドラマ「ドクター・フー」は、主人公のドクターと呼ばれる異星人が、地球人の仲間とともに時空を行き来きする冒険物語である
あるいは、タイムトラベルによる歴史の改変で、時間軸が分岐して、元の時間線と並行した別の時間線が生まれるとする、「パラレルワールド」の概念もあります。例えば、現在いる時間線から、タイムトラベルでたどり着いた先は、元々いた時間線に酷似した「別の時間線」であり、別の時間線で発生した出来事は、元の時間線には影響しないという考え方です。
パラレルワールドは、SFではよく知られた概念ですが、実際に物理学の世界でも、理論的な可能性が語られています。現在の宇宙は、主に「正物質(陽子や電子など)」で構成されていますが、「反物質(反陽子や反電子など)」の存在が、微量確認されています。反物質は、ビッグバンによって出現しましたが、同時に出現した正物質と相互に反応して、ほとんどの反物質は消滅してしまいました。そして、正物質と反物質の間に微妙な量のゆらぎがあり、正物質の方がわずかに多かったため、その残りが、この宇宙を構成する物質となりました。そのために、現在の宇宙は、ほぼすべてが正物質で構成されているというのです。ビッグバンの過程において、この宇宙以外にも、他の宇宙が無数に泡のごとく生じており、他のパラレルワールドでは、逆に「反物質のみから構成される世界」が存在するのではないか、という仮説が提示されています。いずれにせよ、パラレルワールドは架空の話なので、タイムパラドックスの疑問に答える術はないのかもしれません。
・参考文献
1) 遠藤龍介著「よく見る相対論の誤解」東北物理教育26, 2−9, 2017
2) 神森眞/田久保海誉 共著「テロメア研究最近の進歩」日老医誌2004;41;365−368
3) 管乃廣「物理科学が解き明かす時間の秘密」株式会社アントレックス(2010年発行)
4) くられ「アリエナクナイ科学ノ教科書〜空想設定を読み解く31講〜」ソシム株式会社(2017年発行)
5) 佐藤勝彦「カラーでわかる!相対性理論」PHP研究所(2009年発行)
6) 竹内薫「図解入門 よくわかる最新宇宙論の基本と仕組み」株式会社秀和システム(2007年発行)
7) 福江純「そこが知りたい天文学」株式会社日本評論社(2008年発行)
8) 本川達雄「ゾウの時間 ネズミの時間―サイズの生物学」中央公論社(1992年発行)
9) 松田卓也/二間瀬敏史 共著「時間にはなぜ方向があるのか?―その宇宙論的解答―」日本物理学会誌 第38巻 第8号(1983)
10) 山田俊弘「〈正義〉の生物学 トキやパンダを絶滅から守るべきか」講談社サイエンティフィク(2020年発行)
11) Reto U.Schneider「狂気の科学」東京化学同人(2015年発行)
12) Reto U.Schneider「続 狂気の科学」東京化学同人(2018年発行)