・界面化学
【目次】
(1) 界面化学とは何か？
界面化学とは、2つの物質が接する境界に生じる現象を扱う学問分野のことです。研究領域がコロイド化学と近いため、学会や雑誌などでは、両者を合わせて扱われることも多いです。コロイドは、その構造により、「高分子コロイド(polymer colloid)」や「会合コロイド(association colloid)」、「分散コロイド(dispersed colloid)」に分類することができます。高分子コロイドは、その名の通り、高分子のコロイドのことです。会合コロイドは、界面活性剤が集合してできた「ミセル(micelle)」が分散しているコロイドです。分散コロイドは、不溶性の微粒子が分散しているコロイドのことです。特に、分散コロイドでは、分散質と分散媒が、それぞれ明確に分かれているので、系の中に相境界としての「界面(interface)」を含んでいます。また、分散媒が気相のときは、その界面を特に「表面(surface)」と呼んでいます。私たちは「表面張力(surface tension)」という言葉をよく使いますが、もっと広い意味では、表面張力ではなく「界面張力(interfacial tension)」という言葉を使います。
表.1 表面と界面の違い
|
表面(surface) |
界面(interface) |
|
気相と液相の境界面 気相と固相の境界面 |
気相と液相の境界面 液相と液相の境界面 液相と固相の境界面 固相と固相の境界面 固相と気相の境界面 |
コロイドの性質を調べるときは、そのコロイド粒子の界面を調べることが多いです。粒子の単位質量当たりの表面積を「比表面積(specific surface area)」といいます。微粒子系では、比表面積は通常「m2/g」の単位で表します。例として、密度ρ g/m3の物質1 gを、半径r mの微粒子N個に粉砕したとします。コロイドの大きさに粉砕しても、質量は保存されるので、このときの比表面積をS m2/gとすると、次のようになります。
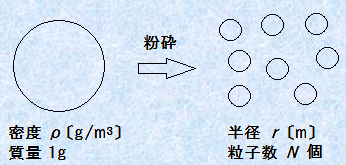
図.1 コロイド粒子の比表面積
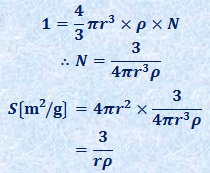
これより、粒子の大きさと比表面積Sの間には、
という関係があることが分かります。この式は、一体どのようなことを意味するのでしょうか？例えば、物質の密度をρ＝3×106 g/m3とすると、r＝10 nmのときでは、比表面積はS＝100 m2/gにもなります。たった1 gのコロイド粒子でも、その表面積は一軒家の敷地面積ぐらいの広さがあるのです。このようにコロイド粒子には、半径rと反比例して、比表面積Sが大きくなるという性質があります。
また、コロイドにおける表面の重要性を示すもう1つの計算をしてみましょう。一辺Lの立方体粒子に、一辺l (L＞l
)の立方体分子が詰まっているという、単純な粒子モデルを考えます。構成分子の中で、表面に顔を出している分子の割合を幾何学的に計算してみましょう。粒子中の分子の総数Nは、
個と表せます。そして、表面にある分子の総数nは、
個と表せます。したがって、表面原子の割合f は、次のように計算できます。
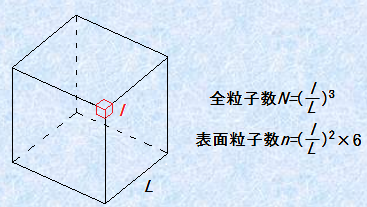
図.2 コロイド粒子の表面原子数の割合
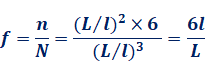
これより、粒子の大きさと表面原子の割合f の間には、
という関係があることが分かります。例えば、立方体分子の大きさをl＝4 nmとすると、L＝10 nmのときにはf＝0.24、L＝3 nmのときにはf＝0.80となります。このようにコロイド粒子には、粒子の大きさと反比例して、表面原子の割合が大きくなる性質もあります。コロイド粒子は比表面積が大きく、表面原子の割合も大きいので、コロイドの物性として、粒子表面の性質がよく現れるのです。
また、表面は分子的に見て、内部とは異なる状態にあります。すなわち、内部の分子では、全方位に分子間力が均等に作用していて、その物質としての凝集力は、均一に働いています。しかし、表面にある分子は、分子間力が均一に働かず、その分子間力の合力は、内部に向かう不均一の力となるのです。
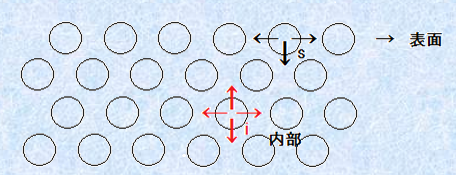
図.3 内部分子(i)と表面分子(s)に働く分子間力
この不均一な分子間力は、マクロには表面張力を発生させ、また隣接する相からの分子やイオンの吸着、固体面の液体によるぬれの原因となります。さらに、イオンの界面への吸着は、界面に電荷を生じさせます。これらの表面張力や吸着、ぬれ、界面電気は、表面積に比例する現象であるので、比表面積の大きいコロイドでは、顕著に現れてきます。そして、これらの現象が、コロイドの物性を大きく左右することになるのです。例えば、鉄Feは釘のように大きいままだと、火で炙っても簡単には燃えません。しかし、スチールウールはマッチで着火すると、花火のように燃えます。さらに、鉄Feをコロイドの大きさにすると、空気中に取り出しただけで、自然発火するようになります。身近でよく知られた鉄Feでも、コロイドの大きさでは、物性が全く違ってくるのです。
図.4 鉄Feをコロイドの大きさにすると、空気に触れるだけで自然発火する
(2) 吸着
気体と固体、気体と液体、液体と固体、液体と液体などが接しているとき、その間には界面ができます。この界面に原子や分子、イオンなどの微粒子が近付くと、この微粒子は、2つの相を構成する粒子と引き合います。しかし、たいていはどちらか一方と引き合う力の方が強いので、引き合う力の強い方へ引き付けられます。そして、その力が非常に強いとき、微粒子は一方の相の表面にくっついて、離れなくなります。このように、ある物体の界面における濃度が、周囲よりも増加する現象を「吸着(adsorption)」といいます。
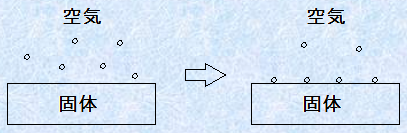
図.5 固体表面への気体分子の吸着
吸着は、すべての界面で起こりうる一般現象です。吸着する微粒子を「吸着質(adsorbate)」といい、それに対して吸着される物質を「吸着媒(adsorbent)」といいます。吸着は、日常的にもよく利用されている現象であり、身近にある吸着媒は、活性炭やシリカゲルです。冷蔵庫の臭いを除く脱臭剤が市販されていますが、中を調べてみると、粒状の活性炭が入っているはずです。活性炭は臭い分子を吸着し、脱臭してくれるのです。また、缶や瓶の中のお菓子には、紙袋などに入れた乾燥剤が入っています。その中を調べてみると、白い粒が入っており、ときには青い粒で、少し赤みがかかっていることもあります。これはシリカゲルであり、シリカゲルは、水分子を吸着してくれるのです。青色や赤色になっているのは、シリカゲルに、塩化コバルト(II) CoCl2が配合されているからです。コバルト(II)イオンCo2+ は、無水CoCl2のときは青く、水H2Oを吸って六水和物CoCl2･6H2Oになると赤くなる性質があり、シリカゲルの吸湿能を示す指示薬になっています。
CoCl2(青) ＋ 6H2O → CoCl2･6H2O(赤)
活性炭とシリカゲルに共通していることは、両者とも固体表面に微細な凹凸のある多孔質物質で、比表面積が非常に大きいということです。その比表面積は、製造方法や保存方法の仕方などによって異なりますが、たった1 gの活性炭でも700〜1500 m2/g、シリカゲルでは500〜750 m2/gの値を取ります。吸着は固体表面で行われるので、比表面積が大きいほど、一定量の固体の吸着能は大きくなります。
図.6 活性炭は、700〜1500 m2/gの比表面積を持つ
また、活性炭とシリカゲルで異なるところは、吸着しやすい物質の違いです。活性炭は炭素Cからできているので、疎水性の有機化合物に対する親和性が大きく、有機化合物に対する吸着能が非常に大きいです。一方で、シリカゲルは化学式ではSiO2･nH2O(0＜n＜1)で表されるので、化学結合に極性があり、結合に極性のある水分子をよく吸着してくれます。したがって、シリカゲルを脱臭剤として使用しても、有機化合物である臭い分子をあまり吸着してくれず、逆に活性炭を乾燥剤として使用しても、水分子をあまり吸着してくれません。吸着媒にも、適材適所があるのです。
(i) 吸着の熱力学
微粒子の吸着が起きると、微粒子の運動は制限され、微粒子は吸着媒の表面に束縛されることになります。つまり、吸着反応のエントロピーの変化ΔSは、吸着質分子の運動の自由度が減少するので、ΔS＜0になります。また、吸着が起こるということは、自由エネルギーの変化はΔG＜0でなければならないので、ギブスの自由エネルギー式ΔG＝ΔH-TΔSより、次のようになります。
吸着反応はΔS＜0なので、ギブスの自由エネルギーの式ΔG＝ΔH-TΔSにおける「-TΔS 」の項は、必ず正の値になります。そこで、ΔG＜0になるためには、少なくともΔH＜0でなければならないのです。つまり、すべての吸着反応は、ΔH＜0の発熱反応になります。吸着反応は発熱反応なので、ル･シャトリエの法則より、温度を上げていくと、吸着量は減少していきます。温度が低いほど、吸着反応が起こりやすいのです。
しかしながら、吸着が発熱反応ということは、吸着質と吸着媒との間に何らかの相互作用が働いて、吸着質が安定化するような仕組みになっていなければなりません。それらの相互作用として、分子間力による「物理吸着(physisorption)」と、化学結合による「化学吸着(chemisorption)」の2つがあります。物理吸着は、吸着が化学吸着より弱いため、温度を上げたり希釈したりすると容易に脱着が起こるので、吸着反応は可逆的です。一方で、化学吸着したものは脱着しにくく、不可逆性が強いです。また、化学吸着は一種の化学反応であるので、吸着に際して活性化エネルギーを必要とし、吸着速度は遅くなります。次の表.2に、物理吸着と化学吸着の特性の比較を示します。
表.2 物理吸着と化学吸着
|
|
物理吸着 |
化学吸着 |
|
吸着力 |
弱い |
強い |
|
相互作用 |
分子間力 |
化学結合 |
|
吸着熱 |
数kJ |
数十kJ |
|
可逆性 |
可逆的 |
不可逆的 |
|
選択性 |
なし |
あり |
|
吸着速度 |
速い |
遅い |
|
活性化エネルギー |
なし |
あり |
化学吸着は、金属表面への水素H2や酸素O2の吸着で見られます。この場合、金属表面で分子から原子への解離が起こり、解離吸着した原子は、非常に反応しやすい状態になっています。エチレンC2H4の水素化において、ニッケルNiなどの金属が必要となるのは、このためです。この反応において、金属の吸着媒は触媒として作用しています(脂肪族炭化水素(アルケン)を参照)。
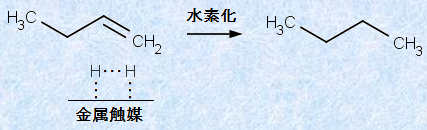
図.7 アルケンの水素化
(ii) 吸着等温線
固体への気体分子の吸着量を求めるためには、吸着前の気体の圧力P0を測り、固体を入れて吸着させたあとの気体の圧力Pを測ります。P0-Pが、吸着による圧力の変化量になるので、吸着した気体の物質量をnとすると、次のような関係が成り立ちます。この式より、吸着した気体の物質量nを求めることができます。
また、溶液から固体への吸着量を求めるには、気体の場合の圧力の代わりに、溶質の濃度を使います。吸着前の溶質濃度をC0とし、吸着後の溶質濃度をCとすれば、吸着した溶質の物質量nは、次のように求めることができます。
これらの式を用いることで、吸着量のグラフを作成することができます。まず、一定温度で、吸着質の圧力または濃度を変えて、吸着量を測定します。それから、吸着量と吸着後の圧力または濃度をそれぞれ縦軸と横軸に取って、グラフを書きます。このようにして作成したグラフを、「吸着等温線(adsorption isotherm)」といいます。作成した吸着等温線からは、色々な情報を読み取ることができます。例えば、吸着等温線の形は、気体吸着と溶液吸着ではかなり違ってきます。よく見られる吸着等温線の型を次の図.8に示しました。
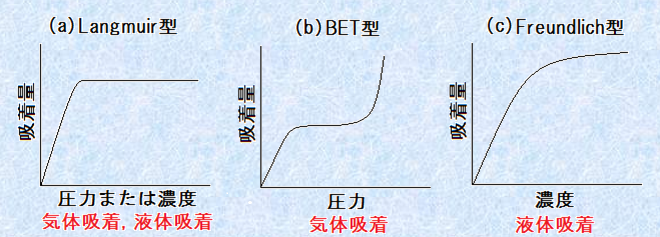
図.8 主な吸着等温線の型
図.8の(a)をLangmuir型(ラングミュア型)といいます。Langmuir型は、圧力あるいは濃度が増加しても、ある値以上では吸着量が一定になってしまうことを示します。これは、気体吸着と溶液吸着の両者で見られる型です。(b)はBET型といい、アメリカの研究者であるブルナウアーとエメット、テラーのイニシャルを取ったものです。BET型は、主に気体吸着で見られる型です。(c)はFreundlich型(フレンドリッチ型)といい、濃度が増加するにつれて、吸着量が平方根関数的に増加していきます。これは、主に溶液吸着で見られる型です。
(iii) 吸着等温式
吸着等温線を、数式で表したものを「吸着等温式(adsorption isotherm)」といいます。Langmuir型とBET型ついては理論式が、Freundlich型については実験式が与えられています。
(iii-1) Langmuirの吸着等温式
吸着質の吸着量をΓ (ガンマ)、平衡濃度をcとするとき、Langmuirの吸着等温式は次のように表されます。ここで、aとΓmは定数です。定数aは吸着熱に対応する量を表し、定数Γmは飽和吸着量を表しています。
気体吸着では、平衡濃度cの代わりに、平衡圧pを使います。Langmuirの式は、吸着質分子が単分子層吸着する場合を想定しており、固体表面に吸着質分子がすべて吸着してしまうと、もうそれ以上は吸着する場所がなくて、吸着できなくなってしまうことを表します。それ故に、Langmuir型の吸着等温線は、ある値以上では吸着量が一定になり、吸着量が飽和してしまうのです。
(iii-2) BETの吸着等温式
標準状態における気体分子の吸着量をV、平衡圧をp、飽和蒸気圧をp0とするとき、BETの吸着等温式は、次のように表されます。ここで、CとVmは定数です。定数Vmは単分子層として吸着する量を表し、定数CはLangmuirの式の定数aに相当する量を表しています。
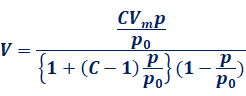
BETの式は、多分子層吸着を想定したものです。すなわち、吸着によって最初に単分子層ができ、そのあとに単分子層の上に気体分子が何層にも吸着していくことを表しています。定数Vmは、最初の単分子層の完結する吸着量に相当します。それ故に、BET型の吸着等温線は、最初はLangmuir型に近いグラフとなり、そのあとに吸着量が指数関数的に増加するグラフとなるのです。
(iii-3) Freundlichの吸着等温式
吸着質の吸着量をΓ、平衡濃度をcとするとき、Freundlichの吸着等温式は、次のように表されます。ここで、kとnは定数です。
この式は、経験的に導出された式です。定数の物理的意味は、はっきりしていません。吸着媒が、活性炭やシリカゲルのような多孔質物質である場合によく当てはまります。これらの吸着媒は、表面構造が複雑で、吸着する場所がたくさんあり、それぞれの場所でLangmuirの式が成立し、それらの和がFreundlichの式になると解釈できます。Freundlichの吸着等温式は、実験データを整理するのに便利です。
(3) 表面張力
「表面張力(surface tension)」とは、「表面を引っ張る力」と書くように、液体の表面を内部へと引っ張って、表面積をできるだけ小さくしようとする力のことです。表面張力は、「界面張力(interfacial tension)」の一種であり、正確な定義は、「液体表面分子の持つ、内部に比べて過剰な単位面積当たりの自由エネルギー」になります。液体の表面積をできるだけ小さくしようとする力が働くのは、過剰な自由エネルギーを持つ表面分子が、液体の内部へ向かって引っ張られるからです。自由エネルギーは小さいほうがより安定であり、表面分子は内部へと引っ張られます。
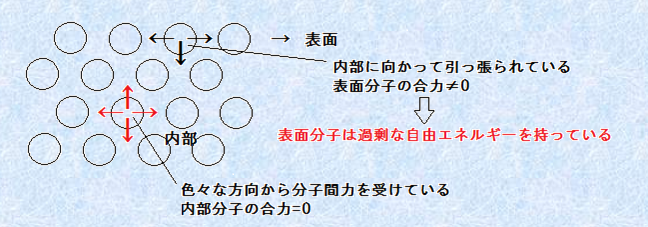
図.9 表面張力発生のメカニズム
液体の分子間には、分子間力が作用しており、それぞれは互いに引き合って凝集しようとします。液体内部の分子は、色々な方向から分子間力を受けて安定化しているのに対して、表面にある分子は、内部の分子に触れていない部分だけ、他の分子による分子間力を受けません。その結果、表面分子は過剰な自由エネルギーを持つことになり、液体は表面積が最も小さくなる球形になろうとするのです。無重力下では、水滴は綺麗な球形になることが知られていますが、これは水H2Oの表面張力が影響しています。
図.10 無重力下では、水滴は綺麗な球形になることが知られている
また、表面張力γによる自由エネルギーの変化量をdG、表面積の変化量をdSとします。表面張力によって、液体の表面積は小さくなり、自由エネルギーは減少します。つまり、表面張力による仕事量が、自由エネルギーの変化量に相当するので、次のような式が成り立ちます。
この式を積分すると、次のような式になります。この式より、表面張力γは、「比表面自由エネルギー」であるということが分かります。すなわち、表面張力γの単位は、SI単位系では「J/m2」と表せるのです。
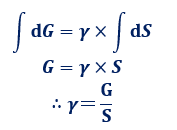
表面張力の単位は「J/m2」ですが、表面という2次元の面を考えて、表面張力を「その面内に作用する単位長さ当たりの力(N/m)」と見なしても問題ありません。ただし、表面張力の単位は、習慣的にSI単位系ではなく、CGS単位系を用いて表すことが多く、一般的にはCGS単位系の「dyn/cm」という単位を用います。ちなみに、1 dynは1 gの物質に1 cm/s2の加速度を与える力のことで、1 dyn＝10-5 Nです。次の表.3に、液体の表面張力のデータを示します。この表には、比較のために蒸発熱のデータも併記しました。両者とも、分子間力に対応した物性ではありますが、前者は自由エネルギー、後者はエンタルピーと関係しています。
表.3 純粋液体の表面張力と蒸発熱
|
|
表面張力(20℃) (dyn/cm) |
蒸発熱(25℃) (kJ/mol) |
|
水銀 |
470 |
59.1 |
|
水 |
72.8 |
43.9 |
|
ベンゼン |
28.9 |
33.8 |
|
クロロホルム |
27.2 |
31.8 |
|
四塩化炭素 |
26.8 |
32.8 |
|
シクロヘキサン |
25.0 |
33.0 |
|
n-ペンタン |
20.3 |
29.5 |
|
エタノール |
17.0 |
26.6 |
水H2Oは、水銀Hgを除くすべての液体のうちで、表面張力が一番大きいです。この理由は、水分子H2Oは、分子間で強力な水素結合を形成しているからです。ちなみに、水銀Hgの表面張力が大きいのは、金属結合によります。また、表面張力は、温度が上昇すると低下していきます。これは、温度が上がることで、分子の熱運動が活発になり、分子間力による相互作用の影響が小さくなるからです。一般的に分子間に相互作用する分子間力が大きいほど、液体の表面張力は大きくなります。
(i) 曲面の表面張力
液中の球状気泡に空気を吹き込んで、半径drだけ膨張させたときの仕事を考えます。このときの圧力の増加分をΔP、体積の変化量をdVとすると、膨張させたときの仕事はΔP×dVとなります。また、表面張力をγ、表面積の変化量をdSとすると、表面拡張の仕事はγ×dSとなります。さらに、
、
なので、両式をそれぞれを半径rについて微分すると、
、
となります。エネルギーの総和が等しいことより、
の関係が成り立つので、これをΔPについて式変形すると、次のような「ヤング･ラプラスの式(Young-Laplace formula)」が得られます。
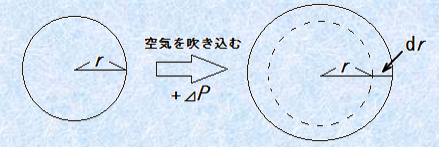
図.11 表面拡張仕事のモデル図
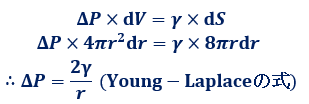
なお、このときのΔPは、「気泡の膨張に使われた」として計算しましが、仮に「膨張の仕事に使わず、その仕事分のエネルギーを内部に保持している」と考えると、ΔPは外圧と内圧の圧力差であると見なすこともできます。つまり、外圧をPg、液体内部の圧力をPlとすると、Pl＞Pgなので、ΔP＝Pl−Pgとなります。
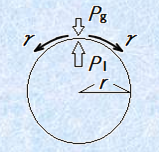
図.12 球状気泡の圧力差ΔP
この図.12のモデルにも、ヤング･ラプラスの式は成立することが知られています。ヤング･ラプラスの式は、球状の界面間に生じている圧力差ΔPを求めるのによく用いられる式です。この式において、表面張力γと外圧Pgは定数と見なすことができるので、この式が表していることは、球体の大きさrに反比例して、内部に加わる圧力Plが大きくなるということです。つまり、小さい球体ほど、内部には大きな圧力が生じているのです。ゴム風船を膨らませるときに、半径が小さいときはなかなか風船が膨らまなくて大変ですが、ある程度風船が膨らんで半径が大きくなると、簡単に膨らませられるようになるのはそのためです。この結果を示すシャボン玉の実験があるので、次の図.13に紹介しておきます。大きなシャボン玉と小さなシャボン玉を連結します。コックを開くと、これらのシャボン玉はどうなるでしょうか？
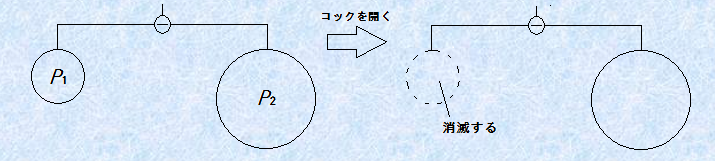
図.13 シャボン玉の実験
大きなシャボン玉には、たくさんの空気が充填されているので、圧力はP2＞P1のような気がして、コックを開くと大きなシャボン玉から小さなシャボン玉へと、空気が流れるような気がします。しかし、結果は意外にも逆になり、小さなシャボン玉から大きなシャボン玉へと、空気の流れが生じるのです。これは、ヤング･ラプラスの式より、半径の小さい球体の方が、内部の圧力が大きいからです。つまり、現実には圧力はP1＞P2であり、小さいシャボン玉は消滅してしまいます。
(ii) 溶液の表面張力
これまでは、純液体の表面張力を考えてきましたが、溶液の表面張力も、同様にして定義することができます。ここでは、溶媒として最もよく用いられ、表面張力が特に大きい水H2Oを対象とします。水溶液の表面張力では、水溶液の表面に、溶質の吸着が起こることに注意しなければなりません。次の図.14に、様々な水溶液の表面張力を示しました。水溶液の表面張力の濃度変化は、溶質の種類により、大きく2種類に分けることができます。すなわち、濃度cが増すと水溶液の表面張力γが減少する場合と、濃度cが増すと表面張力γが増加する場合の2種類です。前者は有機化合物の場合によく現れ、後者は無機塩の場合によく現れます。前者のように、濃度増加によって表面張力が低下する現象を「界面活性(surface active)」といいます。また、後者のように表面張力が増加する現象を「界面不活性(surface negative)」といいます。また、曲線(a)のように表面張力の低下が顕著で、γ- c曲線に折れ曲がりが生じるような溶質を「界面活性剤(surfactant)」といいます。界面活性剤は、分子中に親水基と疎水基を含んでおり、疎水基を気相に向けて、表面に吸着する性質があります。
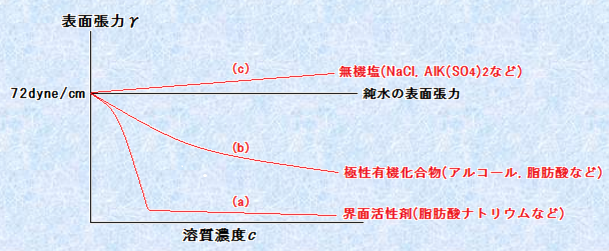
図.14 水溶液の表面張力の溶質濃度依存性
界面活性のある物質については、いずれも分子の中に、疎水基と親水基を持っています。したがって、これらの物質は表面に吸着する性質を持つので、溶質濃度の増加に伴って気相に触れる表面の水分子数が減少し、表面張力が大きく低下するのです。ただし、(a)と(b)のグラフは、かなり特徴が違います。(a)の界面活性剤は、親水基部分が電解質であり、完全な電荷を持っているのに対し、(b)の極性有機化合物は、親水基部分が分極した共有結合で、弱い部分電荷しか持っていないためです。したがって、両者の表面吸着能の比べると、完全な電荷を持っている界面活性剤の方が圧倒的に強く、そのために濃度が少し増加しただけで、大きく表面張力を低下させることができるのです。また、(a)の界面活性剤は、グラフに屈曲点があります。この屈曲点は、表面吸着が満員になったということを表しています。この屈曲点のことを、「臨界ミセル濃度(critical micelle concentration：cmc)」といいます。これ以上の濃度では、界面活性剤は表面吸着ができなくなり、ミセルを作り始めます。
界面不活性な物質については、電解質である無機塩があります。無機塩は、水中では電離してイオンとなって溶けていますが、これらのイオンは、周囲を水分子に取り囲まれ、水和されることで安定化しています。したがって、これらのイオンが表面に出てくることは、水和してくれる水分子が減少することに繋がるので、イオンが表面に出てくると、かえって不安定になってしまいます。また、これと同じことが水分子にもいえ、水分子は分子間で水素結合をするよりも、より強力なクーロン力を持つイオンと相互作用している方が安定です。つまり、無機塩のイオンは、界面活性のある物質と異なり、表面吸着が起こることはありません。その結果、表面が純水に近い状態であるのに対して、内部は水分子とイオンが相互作用して安定化しているので、表面と内部のエネルギー差はかえって大きくなり、表面張力が増加してしまうのです。
(4) ぬれ
「ぬれ(wetting)」は、界面化学では非常に重要な界面現象の1つです。吸着は、気体分子あるいは溶質粒子が固体表面や液相の界面に取り込まれる現象をいいます。一方でぬれは、固体表面に液体が付着する現象をいいます。ぬれは、化学的には「固体-気体界面が固体-液体界面に置き換わること」と定義されます。この定義によって、ぬれは大きく次の3型に分類することができます。
図.15 ぬれの3型
ぬれが起こる際、固体-気体界面が固体-液体界面に置き換わるので、熱力学的には自由エネルギーの変化を生じるはずです。界面張力は、界面をできるだけ小さくしようとする力のことですが、別の定義では、単位面積当たりの自由エネルギーであったことを思い出してください。つまり、界面の単位面積当たりの自由エネルギー変化ΔG/Sを考えれば、自由エネルギーGの代わりに界面張力γを使って、ぬれを考えることができるのです。
(i) 付着ぬれ
大きな固体に少量の液体が接した状態を「付着ぬれ(adhesional wetting)」といいます。付着ぬれは、固体-気体界面および液体-気体界面の2つが、固体-液体界面に置き換わることで起こります。付着ぬれの自由エネルギー変化ΔGを考えてみましょう。固体-気体界面に働く界面張力をγSG、液体-気体界面に働く界面張力をγLG、固体-液体界面に働く界面張力をγSLとすると、次のように表せます。ここで、S・L・Gは、それぞれ「固体(solid)」、「液体(liquid)」、「気体(gas)」を表します。
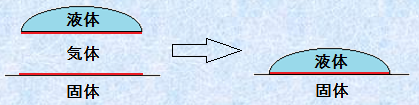
図.16 付着ぬれ
(ii) 浸透ぬれ
管の内部に液体が浸透していく状態を「浸透ぬれ(penetration wetting)」といいます。浸透ぬれの自由エネルギー変化ΔGを考えてみましょう。浸透ぬれでは、固体-気体界面が固体-液体界面に置き換わっているので、次のように表せます。
図.17 浸透ぬれ
(iii) 拡張ぬれ
液体が固体表面に拡がっていく状態を「拡張ぬれ(spreading wetting)」といいます。拡張ぬれの自由エネルギー変化ΔGを考えてみましょう。拡張ぬれでは、固体-気体界面が固体-液体界面および液体-気体界面の2つに置き換わっているので、次のように表せます。ただし、固体をぬらす液体は、十分に薄い膜であると考えます。
図.18 拡張ぬれ
(iv) ぬれの熱力学
液体や固体の物質が、気体のように拡散せずにまとまりを維持するのは、それらの内部の原子や分子同士が互いに引き合っているからです。特に表面では、その力が物質の内部に向かう力として働き、表面張力となって現れます。液体の場合では、自重と表面張力のつり合いによって外形が定まりますが、固体の場合では、固有の外形を維持する力が強いため、その表面張力は観察されにくいです。しかし、次の図.19で示した接触角と界面張力との関係を表す、イギリスの物理学者トマス・ヤングによる「ヤングの式(young formula)」を使うことで、固体の界面張力を表すことができます。固体・液体・気体の三相が平衡状態にあるとき、接触角をθとすると、液滴のふちにおける3つの界面張力γがつり合っていることから、次のようなヤングの式が導けます。
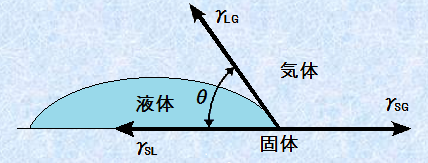
図.19 ヤングの式
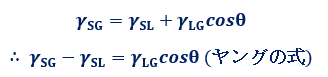
このヤングの式を使って、付着ぬれ・浸透ぬれ・拡張ぬれのそれぞれの式を変形すると、自由エネルギー変化ΔGは、γLGとcosθだけの式となります。γLGとcosθは実験により測定することができるので、これによって3種類のぬれが起きるか否かの、熱力学的な判断が可能となるのです。
(iv-1) 付着ぬれの熱力学
付着ぬれの自由エネルギー変化は、ΔG＝γSL-(γSG＋γLG)のように表せます。ヤングの式γSG-γSL＝γLGcosθを使って、付着ぬれの式を変形すると、次のようになります。
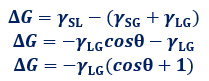
自由エネルギー変化はΔG＜0となれば、ぬれが起きることになります。つまり、上式より0°≦θ＜180°の範囲で、付着ぬれが起きるということが分ります。固体表面のぬれやすさは、接触角θによって定量的に測ることができます。一般的に接触角θが小さいほど、ぬれが良いとされます。接触角θが小さい性質を「親水性(hydrophilic)」、接触角θが大きい性質を「撥水性(water repellency)」といいます。表面張力が小さい固体はぬれにくく、液体が付着したときの接触角θは大きくなります。テフロンなどの撥水性の強い物質の表面では、接触角はθ＝180°近くにもなり、固体表面の上に球形の水滴が載っているような状態になります。接触角がθ＝180°のときはΔG＝0となるため、このような付着ぬれは自然には起こりません。
(iv-2) 浸透ぬれの熱力学
浸透ぬれの自由エネルギー変化は、ΔG＝γSL-γSGのように表せます。ヤングの式γSG-γSL＝γLGcosθを使って、浸透ぬれの式を変形すると、次のようになります。
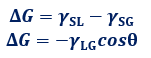
自由エネルギー変化はΔG＜0となれば、ぬれが起きることになります。つまり、上式より0°≦θ＜90°の範囲で、浸透ぬれが起きるということが分ります。浸透ぬれは、いわゆる「毛細管現象(capillary action)」のことです。細い管状物体を水中に浸すと、浸透ぬれが起きて、水H2Oが管の中を上昇してきます。この水H2Oは、浸透ぬれによる安定化の寄与と上昇する水H2Oの重力による不安定化の寄与とがつり合う位置まで上昇します。よくメスシリンダーの目盛りを読むときは、メニスカスの下側を読むようにいわれますが、これは毛細管現象が起きて、液のふちがせり上がることで起こっている現象です。θ≧90°の範囲では、浸透ぬれが起きないので、このときに細い管状物体を導入すると、逆に液体は下降します。このような現象は、水銀Hgに細いガラス管を導入したり、水H2Oに細いプラスチック管を導入したりしたときなどに見られます。
(iv-3) 拡張ぬれの熱力学
拡張ぬれの自由エネルギー変化は、ΔG＝(γSL＋γLG)-γSGのように表せます。ヤングの式γSG-γSL＝γLGcosθを使って、拡張ぬれの式を変形すると、次のようになります。
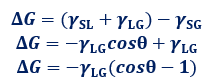
自由エネルギー変化はΔG＜0となれば、ぬれが起きることになります。しかし、これを満たすθは存在しません。液を固体に垂らせば、自然にどこまでも拡がっていくというような拡張ぬれは、現実には起こり得ないのです。θ＝90°は、ぬれの1つの臨界点であり、θ＜90°をぬれが良い、θ＞90°をぬれが悪いなどということがあります。また、液体の界面張力と比べて、固体の界面張力が十分大きいときは、固体に接触した液体は自ら球形になろうとするよりも、固体の表面に拡がろうとしてよくぬれます。物体をぬらしたいときは、液体の界面張力を小さくする界面活性剤を使用すれば、ぬれやすくなります。家庭で洗濯をするときに洗剤を加えるのは、ミセルを作って油汚れを落とすということもありますが、液体の界面張力を小さくして、服の繊維をぬれやすくするという理由もあるのです。
(v) ぬれと一円玉
一円玉は、その成分のすべてがアルミニウムAl だけでできています。アルミニウムAlの密度は2.7 g/cm3なので、水H2O (1.0 g/cm3)よりも重いです。しかし、私たちは一円玉を水面に浮かべることができます。なぜ水H2Oよりも重いはずの一円玉が、水H2Oに浮かぶのでしょうか？この現象について、「水の表面張力で一円玉が浮く」と説明している文献が非常に多いのですが、厳密には少し間違っています。一円玉が水H2Oに浮かぶのは、一円玉に対する水H2Oのぬれが悪いからです。
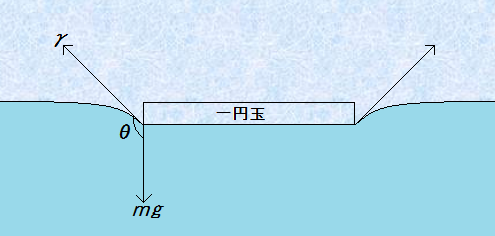
図.20 水面に浮かぶ一円玉
ぬれが悪いと、接触角はθ＞90°となり、水H2Oの表面張力γは上向きに働くようになります。この表面張力γが重力mgの寄与に打ち勝つため、一円玉は水H2Oに浮かぶのです。ちなみに、一円玉の表面は空気中の酸素O2によって酸化されていて、酸化アルミニウムAl2O3の被膜が表面を覆っています。酸化アルミニウムAl2O3は親水性なので、本来一円玉はよくぬれるはずなのです。しかし、ほとんどの一円玉は、ぬれがあまり良くありません。これは、一円玉の表面に皮脂などの油汚れが吸着し、表面が疎水性になっているからだと考えられます。つまり、図.20のように、水面に浮かぶのは、油などで汚れた一円玉だけです。
次に、一円玉のぬれが良い場合を考えてみましょう。油汚れを取り除いた綺麗な一円玉を用意してもいいのですが、一円玉のぬれを良くする簡単な方法があります。一円玉の周囲に、洗剤などの界面活性剤を加えるのです。界面活性剤は、一円玉の表面に対して、親水基を外側に向けた吸着をして、一円玉の表面はぬれの良い親水性になります。
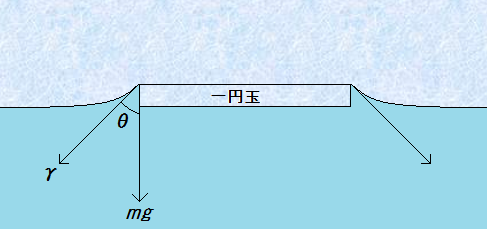
図.21 水に沈む一円玉
ぬれが良いと、接触角はθ＜90°となり、水H2Oの表面張力γは下向きに働くようになります。この表面張力γと重力mgの合力が下向きに働くため、一円玉は水H2Oに沈むのです。したがって、「水の表面張力で一円玉が浮く」というのは、一見すると正しいように思えますが、一円玉のぬれ次第では、図.21のように沈むこともあるので、厳密には間違っているのです。正確には、「汚れた一円玉はぬれが悪く、表面張力が上向きに働くため浮く」というべきです。
・参考文献
1) 北原文雄「コロイドの話」培風館(1984年発行)
2) 北原文雄「界面･コロイド化学の基礎」講談社(1994年発行)